网络中的网络NIN
之前介绍的LeNet,AlexNet,VGG设计思路上的共同之处,是加宽(增加卷积层的输出的channel数量)和加深(增加卷积层的数量),再接全连接层做分类.
NIN提出了一个不同的思路,串联多个由卷积层和'全连接层'(1x1卷积)构成的小网络来构建一个深层网络.
论文地址:https://arxiv.org/pdf/1312.4400.pdf
nin的重点我总结主要就2点:
- mlpconv的提出(我们用1x1卷积实现),整合多个feature map上的特征.进一步增强非线性.
- 全局平均池化替代全连接层
推荐一篇我觉得不错的解读博客:https://blog.csdn.net/hjimce/article/details/50458190
1x1卷积
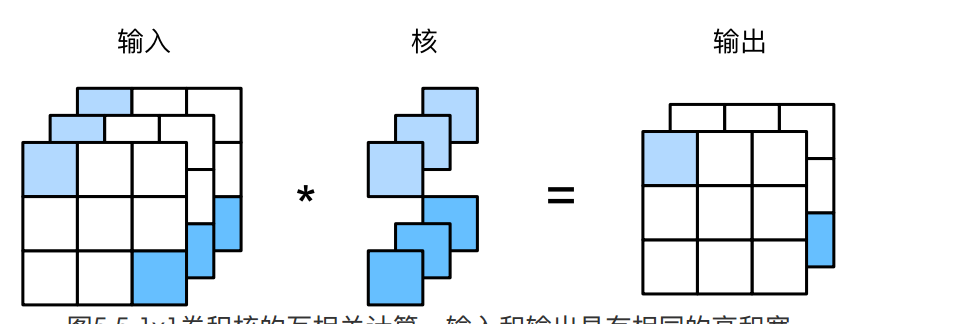
1x1卷积对channel维度上的元素做乘加操作.
如上图所示,由于1x1卷积对空间维度上的元素并没有做关联,所以空间维度(h,w)上的信息得以传递到后面的层中.
举个例子,以[h,w,c]这种顺序为例,1x1卷积只会将[0,0,0],[0,0,1],[0,0,2]做乘加操作.
[0,0,x]的元素和[0,1,x]的元素是不会发生关系的.
NIN结构
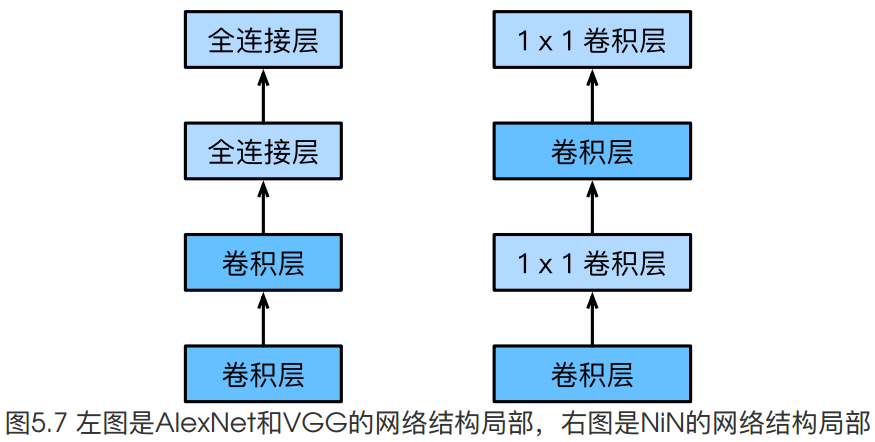
NIN Net是在AlexNet的基础上提出的他们的结构分别如下所示:
AlexNet结构如下:

注意,这个图里的maxpool是在第一二五个卷积层以后.这个图稍微有点误导.即11x11的卷积核后做maxpool,再做卷积.而不是卷积-卷积-池化.
NIN结构如下:
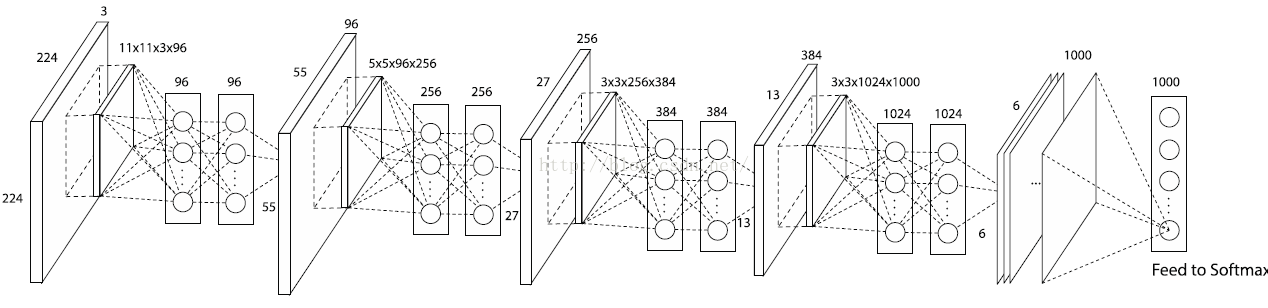
这是网上找的一个示意图,nin的论文里并没有完整的结构图.
这个图有一点不对,最后一个卷积那里应该用的卷积核的shape应该是3x3x384.共1000个,下图红圈处应该是3x3x384x1000,1000,1000.对应到我们的实现,应该是3x3x384x10,10,10.因为我们的数据集只有10个类别.
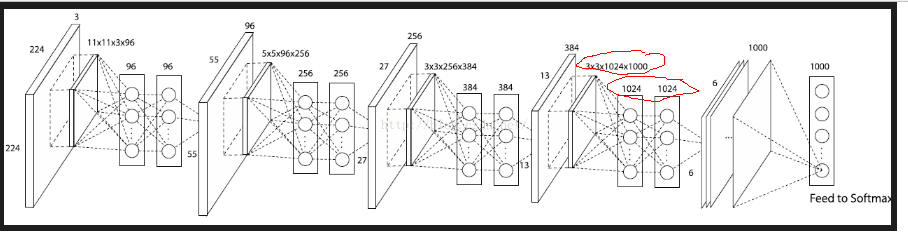
下面我们先来实现卷积部分:
首先我们定义nin的'小网络'模块.即'常规卷积-1x1卷积-1x1卷积'这一部分.
def make_layers(in_channels,out_channels,kernel_size, stride, padding):
conv = nn.Sequential(
nn.Conv2d(in_channels,out_channels,kernel_size, stride, padding),
nn.ReLU(inplace=True),
nn.Conv2d(out_channels,out_channels,kernel_size=1, stride=1, padding=0),#1x1卷积,整合多个feature map的特征
nn.ReLU(inplace=True),
nn.Conv2d(out_channels,out_channels,kernel_size=1, stride=1, padding=0),#1x1卷积,整合多个feature map的特征
nn.ReLU(inplace=True)
)
return conv
然后对于网络的卷积部分,我们就可以写出如下代码
conv1 = make_layers(1,96,11,4,2)
pool1 = nn.MaxPool2d(kernel_size=3,stride=2)
conv2 = make_layers(96,256,kernel_size=5,stride=1,padding=2)
pool2 = nn.MaxPool2d(kernel_size=3,stride=2)
conv3 = make_layers(256,384,kernel_size=3,stride=1,padding=1)
pool3 = nn.MaxPool2d(kernel_size=3,stride=2)
conv4 = make_layers(384,10,kernel_size=3,stride=1,padding=1)
我们来验证一下模型
X = torch.rand(1, 1, 224, 224)
o1 = conv1(X)
print(o1.shape) #[1,96,55,55]
o1_1 = pool1(o1)
print(o1_1.shape) #[1,96,27,27]
o2 = conv2(o1_1)
print(o2.shape) #[1,256,27,27]
o2_1 = pool2(o2)
print(o2_1.shape) #[1,256,13,13]
o3 = conv3(o2_1)
print(o3.shape) #[1,384,13,13]
o3_1 = pool3(o3)
print(o3_1.shape) #[1,384,6,6]
o4 = conv4(o3_1)
print(o4.shape) #[1,10,6,6]
每一层的输出shape都是对的,说明我们模型写对了.如果不对,我们就去调整make_layers()的参数,主要是padding.
卷积部分得到[1,10,6,6]的输出以后,我们要做一个全局平均池化,全局平均池化什么意思呢?
我们先看普通池化,比方说一个10x10的输入,用2x2的窗口去做池化,然后这个窗口不断地滑动,从而对不同的2x2区域可以做求平均(平均池化),取最大值(最大值池化)等.这个就可以理解为'局部'的池化,2x2是10x10的一部分嘛.
相应地,所谓全局池化,自然就是用一个和输入大小一样的窗口做池化,即对全部的输入做池化操作.
所以我们可以实现出全局平均池化部分:
ap = nn.AvgPool2d(kernel_size=6,stride=1)
o5 = ap(o4)
print(o5.shape) #[1,10,1,1]
torch中的nn模块已经提供了平均池化操作函数,我们要做的就是把kernel_size赋值成和输入的feature map的size一样大小就好了,这样就实现了全局平均池化.
全局平均池化的重要意义
用全局平均池化替代全连接层,一个显而易见的好处就是,参数量极大地减少了,从而也防止了过拟合.
另一个角度看,是从网络结构上做正则化防止过拟合.比方说[1,10,6,6]的输入,即10个6x6的feature map,我们做全局平均池化后得到[1,10,1,1]的输出,展平后即10x1的输出,这10个标量,我们认为代表十个类别.训练的过程就是使这十个标量不断逼近代表真实类别的标量的过程.这使得模型的可解释性更好了.
参考:https://zhuanlan.zhihu.com/p/46235425
基于以上讨论,我们可以给出NinNet定义如下:
class NinNet(nn.Module):
def __init__(self):
super(NinNet, self).__init__()
self.conv = nn.Sequential(
make_layers(1,96,11,4,2),
nn.MaxPool2d(kernel_size=3,stride=2),
make_layers(96,256,kernel_size=5,stride=1,padding=2),
nn.MaxPool2d(kernel_size=3,stride=2),
make_layers(256,384,kernel_size=3,stride=1,padding=1),
nn.MaxPool2d(kernel_size=3,stride=2),
make_layers(384,10,kernel_size=3,stride=1,padding=1)
)
self.gap = nn.Sequential(
nn.AvgPool2d(kernel_size=6,stride=1)
)
def forward(self, img):
feature = self.conv(img)
output = self.gap(feature)
output = output.view(img.shape[0],-1)#[batch,10,1,1]-->[batch,10]
return output
我们可以简单测试一下:
X = torch.rand(1, 1, 224, 224)
net = NinNet()
for name,module in net.named_children():
X = module(X)
print(name,X.shape)
输出
conv torch.Size([1, 10, 6, 6])
gap torch.Size([1, 10, 1, 1])
接下来就是熟悉的套路:
加载数据
batch_size,num_workers=16,4
train_iter,test_iter = learntorch_utils.load_data(batch_size,num_workers,resize=224)
定义模型
net = NinNet().cuda()
print(net)
定义损失函数
loss = nn.CrossEntropyLoss()
定义优化器
opt = torch.optim.Adam(net.parameters(),lr=0.001)
定义评估函数
def test():
start = time.time()
acc_sum = 0
batch = 0
for X,y in test_iter:
X,y = X.cuda(),y.cuda()
y_hat = net(X)
acc_sum += (y_hat.argmax(dim=1) == y).float().sum().item()
batch += 1
#print('acc_sum %d,batch %d' % (acc_sum,batch))
acc = 1.0*acc_sum/(batch*batch_size)
end = time.time()
print('acc %3f,test for test dataset:time %d' % (acc,end - start))
return acc
训练
num_epochs = 3
def train():
for epoch in range(num_epochs):
train_l_sum,batch,acc_sum = 0,0,0
start = time.time()
for X,y in train_iter:
# start_batch_begin = time.time()
X,y = X.cuda(),y.cuda()
y_hat = net(X)
acc_sum += (y_hat.argmax(dim=1) == y).float().sum().item()
l = loss(y_hat,y)
opt.zero_grad()
l.backward()
opt.step()
train_l_sum += l.item()
batch += 1
mean_loss = train_l_sum/(batch*batch_size) #计算平均到每张图片的loss
start_batch_end = time.time()
time_batch = start_batch_end - start
train_acc = acc_sum/(batch*batch_size)
if batch % 100 == 0:
print('epoch %d,batch %d,train_loss %.3f,train_acc:%.3f,time %.3f' %
(epoch,batch,mean_loss,train_acc,time_batch))
if batch % 1000 == 0:
model_state = net.state_dict()
model_name = 'nin_epoch_%d_batch_%d_acc_%.2f.pt' % (epoch,batch,train_acc)
torch.save(model_state,model_name)
print('***************************************')
mean_loss = train_l_sum/(batch*batch_size) #计算平均到每张图片的loss
train_acc = acc_sum/(batch*batch_size) #计算训练准确率
test_acc = test() #计算测试准确率
end = time.time()
time_per_epoch = end - start
print('epoch %d,train_loss %f,train_acc %f,test_acc %f,time %f' %
(epoch + 1,mean_loss,train_acc,test_acc,time_per_epoch))
train()
部分输出如下
epoch 0,batch 3600,train_loss 0.070,train_acc:0.603,time 176.200
epoch 0,batch 3700,train_loss 0.069,train_acc:0.606,time 181.160
***************************************
acc 0.701800,test for test dataset:time 11
epoch 1,train_loss 0.069109,train_acc 0.607550,test_acc 0.701800,time 195.619591
epoch 1,batch 100,train_loss 0.044,train_acc:0.736,time 5.053
epoch 1,batch 200,train_loss 0.047,train_acc:0.727,time 10.011
epoch 1,batch 300,train_loss 0.048,train_acc:0.735,time 15.210
可以看到由于没有了全连接层,训练时间明显缩短.