系统不确定性的度量
先来看2个概念.
信息熵 $$h( heta)=sum_{j=0}^n heta_jx_j$$
基尼系数 $$G=1-sum_{i=0}^n p_i^2$$
二者都反映了信息的不确定性,是信息不确定性的不同评价标准.
关于信息熵,在数学之美中,有一段通俗易懂的例子.




sklearn中使用决策树
在sklearn中使用decisiontree时,采用信息熵或者基尼系数,预测准确率并不会有很大差异.
from sklearn.tree import DecisionTreeClassifier tree_clf = DecisionTreeClassifier(max_depth=2, criterion="entropy") tree_clf.fit(X, y)
tree_clf = DecisionTreeClassifier(max_depth=2, criterion="gini") tree_clf.fit(X, y)
决策树原理
比如我们有一组数据,m个样本,n个特征.我们希望经过x次决策(实际上也就是类似与x次if-else判断,每一次if-else判断以后,我们的样本都可以被分成2部分,我们就可以计算这2部分的信息含量(也就是信息熵)),使得所有样本的不确定性最低.不确定性最低的含义也就是:模型最大可能地拟合了我们的数据.
决策树:每一次划分,都希望使得整个系统的不确定性降低,也就是使得每一次决策后使得整个系统的信息熵最低.
在决策时,怎么知道用哪个维度(d)的哪个值(v)去做分割(即if的条件应该如何表达),使得整个系统的信息熵最低呢?
一种朴素的方法,就是穷举,搜索.比如样本X,y.
from collections import Counter
from math import log
def entropy(y):
counter = Counter(y)
res = 0.0
for num in counter.values():
p = num / len(y)
res += -p * log(p)
return res
def try_split(X, y):
best_entropy = float('inf')
best_d, best_v = -1, -1
for d in range(X.shape[1]):
sorted_index = np.argsort(X[:,d])
for i in range(1, len(X)):
if X[sorted_index[i], d] != X[sorted_index[i-1], d]:
v = (X[sorted_index[i], d] + X[sorted_index[i-1], d])/2 #取2个样本的均值作为v
X_l, X_r, y_l, y_r = split(X, y, d, v)
e = entropy(y_l) + entropy(y_r)
if e < best_entropy:
best_entropy, best_d, best_v = e, d, v
return best_entropy, best_d, best_v
上述代码,在每一个维度上(即每一个feature)去做遍历,每次v的取值取两个相邻样本的均值.然后计算系统的信息熵,一一比较.
这样经过一次遍历,就得到了tree_left,tree_right。对tree_left/tree_right再执行上述过程,又可以得到tree_left_l,tree_left_r,tree_right_l,tree_right_r,....依次类推.
这就是决策树的模型训练过程.
很容易理解,如果不限制上述过程的次数(树的深度),势必造成过拟合,因为决策的条件被划分的越来越细. 而且模型的复杂度会很高,训练时间很长.
所以在实际的过程中,通常会进行剪枝操作.
可以参考下面这个图理解一下决策树的决策过程
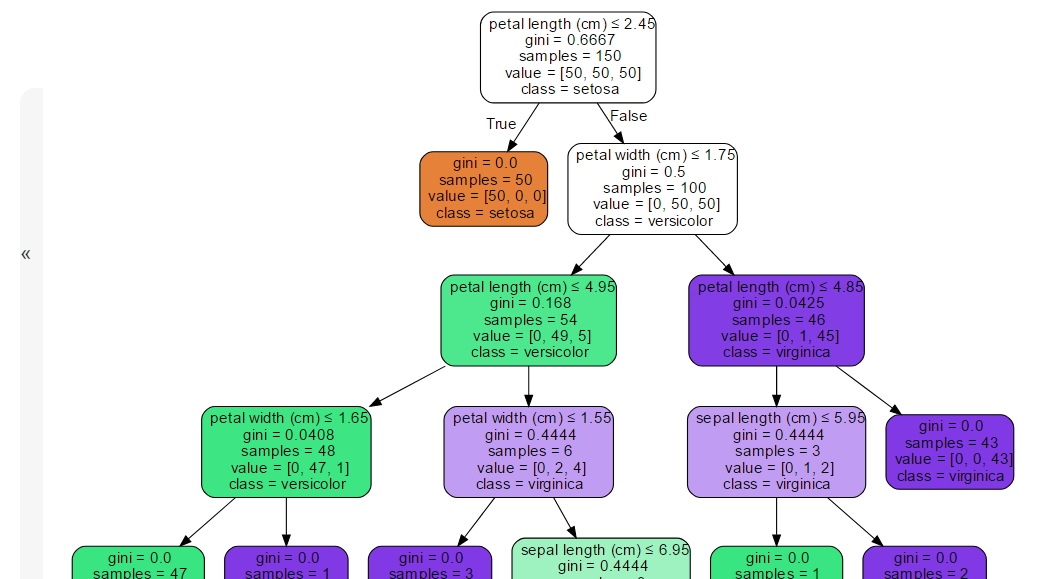
决策树调参
class sklearn.tree.DecisionTreeClassifier(criterion='gini', splitter='best', max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, class_weight=None, presort=False)
max_depth:树的深度.
min_samples_split:某个待决策的节点的最少样本数量.
min_samples_leaf :叶子节点必须包含的最小样本数量
max_features :寻找使系统的不确定性最低的划分时,所需要考虑的最大特征数.
参考上面的分析以及示例图,很容易知道,max_depth越大,复杂度越高.越容易过拟合.
min_samples_split越大,越容易欠拟合,越小越容器过拟合.比如我的min_samples_split设置为1,那肯定树要被划分的很深.
min_samples_leaf 越小越容易过拟合.
更多的参数及含义参考sklearn的官方文档.
决策树的缺点:
对个别数据异常敏感.
容易过拟合.
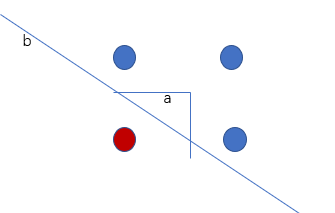
比如上图,b是更好的决策边界,而决策树找出的决策边界很可能是a这条折线. 原理很简单,看一下文章前面描述决策树原理的代码,每一次做tree的split时候,是在某一个维度上,找到一个value,使得分割之后,系统的信息熵最小. 反映到上图的这个二维的样本中来,画出来的分割线就是平行于x轴,y轴(其实就是样本的2个维度)的两条线连起来的折线.
机器学习笔记系列文章列表