SP10707 COT2

裸的树上莫队

其实和普通莫队上一样的，只不过我们要把树转化为线性结构，这就需要欧拉序，我们从根对这棵树进行(dfs)，点进栈时记一个时间戳(st)，出栈时再记一个时间戳(ed)，画个图理解一下

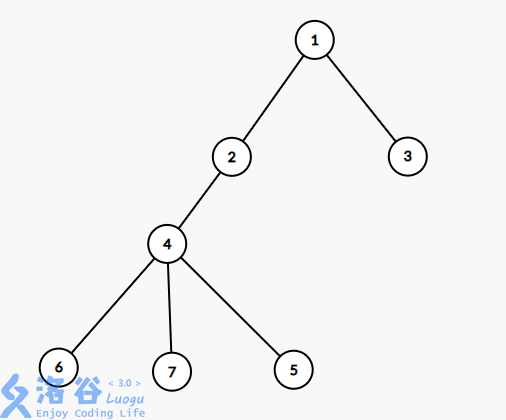
这棵树的欧拉序为((1,2,4,5,5,6,6,7,7,4,2,3,3))，那么每次询问的节点(u,v)有两种情况

1. (u)在(v)的子树中（(v)在(u)的子树中同理），比如(u=6,v=2)，我们拿出((st[2],st[6]))这段区间((2,4,5,5,6))，(5)出现了两次，因为搜索的时候(5)不属于这条链，所以进去之后就出去了，而出现一次的都在这条链上，就都可以统计

2. (u)和(v)不在同一个子树中，比如(u=5,v=3)，这次拿出((ed[5],st[3]))这段区间((5,6,6,7,7,4,2,3))，要保证(st[u]<st[v])，出现两次的可以忽略，然而这次只统计了(5,4,2,3)，所以最后再统计上(lca)就好了

• 至于如何忽略掉区间内出现了两次的点，这个很简单，我们多记录一个(use[x])，表示(x)这个点有没有被加入，每次处理的时候如果(use[x]=0)则需要添加节点；如果(use[x]=1)则需要删除节点，每次处理之后都对(use[x])异或(1)就可以了

• 而欧拉序可以用树剖来求，(lca)也就求出来了，非常的方便

• 排序的话没有区别，可以普通排序，也可以奇偶性排序

• 因为(st,ed)的大小都是(n)，所以取块的大小时要用(2n)，而不是(n)

• 最后要注意的一点就是这个题权值比较大，需要离散化

Code

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cmath>
#include <vector>
#define N 200000
using namespace std;
struct node
{
	int l,r,ll,rr,id,lca;
}q[N+5];
int n,m,a[N+5],st[N+5],ed[N+5],dfn[N+5],f[N+5],num,size[N+5],his[N+5],dep[N+5],son[N+5],top[N+5],c[N+5],tmp,blo,l=1,r,use[N+5],ans[N+5],data[N+5];
vector <int> d[N+5];
void dfs1(int u,int fa)  //树剖第一次深搜
{
	f[u]=fa;st[u]=++num;
	size[u]=1;his[num]=u;
	dep[u]=dep[fa]+1;
	vector <int>::iterator it;
	for (it=d[u].begin();it!=d[u].end();it++)
	{
		int v=(*it);
		if (v==fa)continue;
		dfs1(v,u);
		size[u]+=size[v];
		if (size[v]>size[son[u]])son[u]=v;
	}
	ed[u]=++num;his[num]=u;
}
void dfs2(int u,int to)   //树剖第二次深搜
{
	top[u]=to;
	if (son[u])dfs2(son[u],to);
	vector <int>::iterator it;
	for (it=d[u].begin();it!=d[u].end();it++)
	{
		int v=(*it);
		if (v!=son[u]&&v!=f[u])dfs2(v,v);
	}
}
int Lca(int x,int y)   //树剖求lca
{
	while (top[x]!=top[y])
	{
		if (dep[top[x]]<dep[top[y]])swap(x,y);
		x=f[top[x]];
	}
	if (dep[x]>dep[y])swap(x,y);
	return x;
}
void add(int x)
{
	tmp+=(++c[a[x]]==1);
}
void del(int x)
{
	tmp-=(--c[a[x]]==0);
}
void calc(int x)     //对点进行加入或删除
{
	(!use[x])?add(x):del(x);
	use[x]^=1;
}
int cmp(node x,node y)   //排序
{
	return (x.ll==y.ll)?(x.ll%2==1?x.r<y.r:x.r>y.r):x.l<y.l;
}
int main()
{
	scanf("%d%d",&n,&m);
	for (int i=1;i<=n;i++)
		scanf("%d",&a[i]),data[i]=a[i];
    sort(data+1,data+n+1);
    for(int i=1;i<=n;i++)a[i]=lower_bound(data+1,data+n+1,a[i])-data;  //离散化
	int x,y;
	for (int i=1;i<n;i++)
	{
		scanf("%d%d",&x,&y);
		d[x].push_back(y);
		d[y].push_back(x);
	}
	dfs1(1,0); 
	dfs2(1,1);
	blo=n*2/sqrt(m*2/3);
	for (int i=1;i<=m;i++)
	{
		scanf("%d%d",&x,&y);
		if (st[x]>st[y])swap(x,y);  //保证stx<sty
		q[i].id=i;
		q[i].lca=Lca(x,y);  
		if (q[i].lca==x)    //x,y在以x为根的子树中
		{
			q[i].l=st[x];
			q[i].r=st[y];
			q[i].ll=st[x]/blo;
			q[i].rr=st[y]/blo;
			q[i].lca=0;
		}
		else
		{
			q[i].l=ed[x];
			q[i].r=st[y];
			q[i].ll=ed[x]/blo;
			q[i].rr=st[y]/blo;
		}
	}
	sort(q+1,q+m+1,cmp);
	for (int i=1;i<=m;i++)
	{
		while (l>q[i].l)calc(his[--l]);
		while (r<q[i].r)calc(his[++r]);
		while (l<q[i].l)calc(his[l++]);
		while (r>q[i].r)calc(his[r--]);
		if (q[i].lca)calc(q[i].lca);
		ans[q[i].id]=tmp;
		if (q[i].lca)calc(q[i].lca);
	}
	for (int i=1;i<=m;i++)
		printf("%d
",ans[i]);
	return 0;
}