Description
小强要在N个孤立的星球上建立起一套通信系统。这套通信系统就是连接N个点的一个树。
这个树的边是一条一条添加上去的。在某个时刻,一条边的负载就是它所在的当前能够
联通的树上路过它的简单路径的数量。
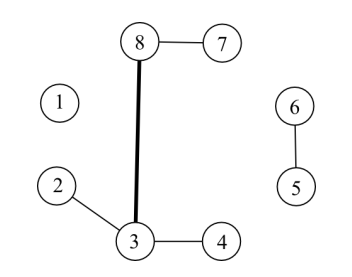
例如,在上图中,现在一共有了5条边。其中,(3,8)这条边的负载是6,因
为有六条简单路径2-3-8,2-3-8-7,3-8,3-8-7,4-3-8,4-3-8-7路过了(3,8)。
现在,你的任务就是随着边的添加,动态的回答小强对于某些边的负载的
询问。
Input
第一行包含两个整数N,Q,表示星球的数量和操作的数量。星球从1开始编号。
接下来的Q行,每行是如下两种格式之一:
A x y 表示在x和y之间连一条边。保证之前x和y是不联通的。
Q x y 表示询问(x,y)这条边上的负载。保证x和y之间有一条边。
1≤N,Q≤100000
Output
对每个查询操作,输出被查询的边的负载。
Sample Input
8 6
A 2 3
A 3 4
A 3 8
A 8 7
A 6 5
Q 3 8
Sample Output
6
解题思路
(lct)维护子树信息裸题。(lct)维护子树信息时需要记录一下虚子树的信息和虚子树+实子树+自己的信息。虚子树信息只有在(link)和(access)的时候才会被改变。具体看代码。
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
using namespace std;
const int MAXN = 100005;
typedef long long LL;
inline int rd(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) {f=ch=='-'?0:1;ch=getchar();}
while(isdigit(ch)) {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
return f?x:-x;
}
int n,q,head[MAXN],cnt,to[MAXN<<1],nxt[MAXN<<1];
int siz[MAXN],Siz[MAXN],ch[MAXN][2],fa[MAXN];
bool rev[MAXN];
inline void pushup(int x){
siz[x]=siz[ch[x][0]]+siz[ch[x][1]]+1+Siz[x];
}
inline void pushdown(int x){
if(rev[x]){
swap(ch[x][0],ch[x][1]);
if(ch[x][0]) rev[ch[x][0]]^=1;
if(ch[x][1]) rev[ch[x][1]]^=1;
rev[x]=0;
}
}
inline bool isroot(int x){
return (x!=ch[fa[x]][0] && x!=ch[fa[x]][1]);
}
void pd(int x){
if(fa[x]) pd(fa[x]);pushdown(x);
}
inline bool check(int x){
return (x==ch[fa[x]][1]);
}
inline void rotate(int x){
int y=fa[x],z=fa[y];bool chk=check(x);
if(!isroot(y)) ch[z][check(y)]=x;
ch[y][chk]=ch[x][chk^1];fa[ch[x][chk^1]]=y;
ch[x][chk^1]=y;fa[y]=x;fa[x]=z;pushup(y);pushup(x);
}
inline void splay(int x){
pd(x);
for(;!isroot(x);rotate(x))
if(!isroot(fa[x])) rotate(check(fa[x])==check(x)?fa[x]:x);
}
inline void access(int x){
for(int y=0;x;y=x,x=fa[x]){
splay(x);if(ch[x][1]) Siz[x]+=siz[ch[x][1]];
if(y) Siz[x]-=siz[y];ch[x][1]=y;pushup(x);
}
}
inline void makeroot(int x){
access(x);splay(x);rev[x]^=1;
}
inline void link(int x,int y){
makeroot(x);makeroot(y);Siz[y]+=siz[x];fa[x]=y;pushup(y);
}
int main(){
n=rd(),q=rd();char op;int x,y;
for(int i=1;i<=n;i++) siz[i]=1;
while(q--){
cin>>op;x=rd(),y=rd();
if(op=='A') link(x,y);
if(op=='Q') {
makeroot(x);access(y);splay(x);
printf("%lld
",(LL)(Siz[y]+1)*(siz[x]-Siz[y]-1));
}
}
return 0;
}