题意
给你一棵 (n) 个点的树,每个节点有两个权值 (a_i,b_i)。
从一个点 (u) 可以跳到以其为根的子树内的任意一点 (v)(不能跳到 (u) 自己),代价是 (a_u imes b_v)。
求每个点跳到任意一个叶子的最小代价。
(nle 10^5, -10^5le a_i,b_ile 10^5)
题解
暴力
考虑暴力 (dp),设 (dp_i) 表示从叶子跳到 (i) 号点的最小代价。
则有转移 (dp_u = min{a_u imes b_v + dp_v})
复杂度 (O(n^2))
优化
发现这是一个裸的斜率优化式子,转移为求多条直线 (y=kx+b) 在直线 (x=a_u) 处的最值((k=b_v, b=dp_v))
好像就是需要维护一个支持动态插入直线的上凸包?是不是写个支持合并的凸包平衡树就行了?
平衡树合并的方法就是启发式合并,把两个 splay 中小的 splay 里面的所有点暴力插入大的 splay。每个点被暴力重新插入后 其所在的 splay 至少增大一倍,所以最多被插入 (log n) 次,一次插入的复杂度最大是 (O(log n)),总时间复杂度就是 (O(n log^2 n))。
综上,可以写平衡树合并来通过此题,但是 CF 这场比赛 (2) 小时让你打 (7) 道题,你写这鬼玩意所需的时间肯定不止 (2) 小时……
观察发现,我们只需要查询 (x=a_u) 处的最值,这个操作好像可以用李超树维护?
于是我们只需要写个支持合并的李超树……
李超树合并与平衡树同理(但是代码量短多了),用启发式合并,把两个李超树中 小的李超树里面的所有点 暴力插入大的李超树,时间复杂度与平衡树合并的复杂度差不多,都是 (O(nlog^2 n))。
代码好写就够了。
upd:今天下午被这么一个问题搞自闭了
因为有些线段树相关的题的空间是 (O(nlog n)) 甚至 (O(nlog^2 n)) 的,而动态开点实际上不会开很多点,所以你可能会适当减少线段树数组的大小。然而因为你少开空间有可能被卡,所以你可能会在本地尝试卡空间。这样做并不保险,你可能本机开了空间上限 (-10MB),但交上去不排除因为测评环境不同而 MLE 的可能,也就是说控制不当你就有爆 (0) 的风险。
为了避免这种风险,我以前有一个用 vector 代替动态开点线段树数组的想法,这样你不但不用手算空间,甚至运行时间都会少一大截。
然后我对这题测试了一波,发现当 (n) 达到 (1w) 出头时就开始 RE 了……
更惊人的是 CF 竟然没有给出 RE 的错误原因(注意上面那个 RE 提交)
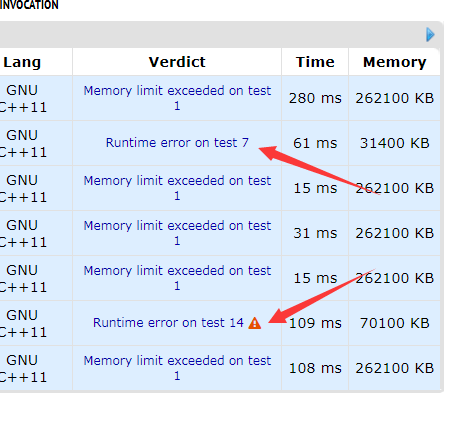
zbl
在本机面向数据和程序二分了一波,发现跑到 ( ext{ins}) 函数时炸了
#define ls tr[o].l
#define rs tr[o].r
struct Tree{
line v; int l,r,siz;
Tree(){v=line(); l=r=0, siz=1;}
};
vector<Tree> tr;
void ins(int &o, int l, int r, line v){
if(!o) o=++cnt, tr.push_back(Tree());
int mid=l+r>>1;
if(cmp(tr[o].v, v, mid)) swap(tr[o].v,v);
if(l==r || tr[o].v.k==v.k || !v.id) return;
double x = cross(tr[o].v,v);
if(x<l || x>r) return;
if(v.k > tr[o].v.k) ins(ls,l,mid,v);
else ins(rs,mid+1,r,v);
pushup(o);
}
经过调试,发现 vector ( ext{pushback}) 到第 (8192) 位后,(o) 这个变量炸了(一输出它就 RE,一用它就 RE,把输出换成其它变量或字符串都能正常输出)
我就不是很懂了,(o) 这个变量到底是咋了?
然后为了输出 (o) 这个变量调了一下午未果,请了很多人也没能解决
有个大佬还主动用 linux 帮我输出 pdb 内部给的错误信息,然而得到的错误信息只有“堆空间删除后再利用”,其它的报错根本不明意义
后来群里还有个人私聊我,说他以前用 vector 开线段树数组也因为这个问题 RE 了,一直没有解决。当时我以为开发者把 c++ STL 写锅了
熬到晚上,有个福州一中的神爷给出了解释?!
vector 是倍增式开空间,即当它 ( ext{pushback}) 到 (2^n(n∈Z)) 时,它会申请一个新的长度为 (2^{n+1}) 的空间,也就是把整个 vector 的地址平移了。
vector 的地址平移会使你目前有关这个 vector 的指针全部失效,因为你的指针指向的是 vector 平移前的地址,现在 vector 已经移走了,你的指针就指空了,输出这个位置就炸了(即堆空间删除后再利用,因为地址本身可能与堆有关)。观察 (o) 这个引用指针指向了谁——发现就是 (ls,rs),即 (tr[o].l,tr[o].r),而 tr 这个 vector 在 ( ext{pushback}) 到第 (8192) 位后就平移了,所以 (o) 这个指针指的地址没了。
换成数学用语就是说:(tr) 是一个 vector,设平移前 (tr) 的起点是一个地址 (a),(o=tr[x].l) 就相当于 ((a+x)->l)。(tr) 平移后 (tr[o].l) 变成了 ((a'+x)->l),但你的 (o) 指针指向的地址还是 ((a+x)->l)。
所以对 vector 要慎用指针之类的东西,防止 vector 地址平移导致指针失效。
看起来大功告成了?
还没完,我改成这么写还是炸:
#define ls tr[o].l
#define rs tr[o].r
struct Tree{
line v; int l,r,siz;
Tree(){v=line(); l=r=0, siz=1;}
};
vector<Tree> tr;
int ins(int o, int l, int r, line v){
if(!o) o=++cnt, tr.pb(Tree());
int mid=l+r>>1;
if(cmp(tr[o].v, v, mid)) swap(tr[o].v,v);
if(l==r || tr[o].v.k==v.k || !v.id) return o;
double x = cross(tr[o].v,v);
if(x<l || x>r) return o;
if(v.k > tr[o].v.k) ls = ins(ls,l,mid,v);
else rs = ins(rs,mid+1,r,v);
pushup(o);
return o;
}
炸的地方没变,还是开到第 (8192) 位就炸了
然后我就开始喷:wcnm 这软件绝对写挂了
冷静分析,发现问题可能出在这:
if(v.k > tr[o].v.k) ls = ins(ls,l,mid,v);
else rs = ins(rs,mid+1,r,v);
有可能是赋值时先取了左边变量的地址,然后再计算右边变量,再赋到左边变量的地址上。这样的话,先前取的 (ls/rs) 的地址在赋值时还是指空了,所以大胆猜测这是炸的原因。
解决方法很显然,用一个变量暂存返回值,再赋给 (ls/rs) 即可。具体见下方代码。
总而言之就是 STL 的写法是真奇怪,经常在内存地址等各种难懂的地方出问题,用户体验不是很好。建议慎用 STL,考前一定要了解使用 STL 可能出现的各种 CE/RE 情况。
不过用 vector 代替数组挺好的,看看测试结果就知道啦:
(500w) 位数组开线段树 
vector 开线段树 
#include<bits/stdc++.h>
#define ll long long
#define pb push_back
#define N 100005
#define lim 100001
#define Lim 200003
const ll inf = 1ll<<60;
using namespace std;
inline int read(){
int x=0; bool f=1; char c=getchar();
for(;!isdigit(c); c=getchar()) if(c=='-') f=0;
for(; isdigit(c); c=getchar()) x=(x<<3)+(x<<1)+(c^'0');
if(f) return x;
return 0-x;
}
int n,a[N],b[N];
ll dp[N];
vector<int> g[N];
struct line{
int k; ll b;
bool id;
line(){k=0, b=0, id=0;}
line(int _k, ll _b, bool _id){k=_k, b=_b, id=_id;}
ll getY(int x){return (ll)k*x+b;}
};
inline bool cmp(line a, line b, int x){
if(!a.id) return 1;
return a.getY(x)>b.getY(x);
}
inline double cross(line a, line b){
return (double)(a.b-b.b)/(b.k-a.k);
}
int rt[N];
struct LiChaoTree{
#define ls tr[o].l
#define rs tr[o].r
struct Tree{
line v; int l,r,siz;
Tree(){v=line(); l=r=0, siz=1;}
};
vector<Tree> tr;
int cnt;
inline void pushup(int o){
tr[o].siz = tr[ls].siz + tr[rs].siz + 1;
}
int ins(int o, int l, int r, line v){
if(!o) o=++cnt, tr.pb(Tree());
int mid=l+r>>1;
if(cmp(tr[o].v, v, mid)) swap(tr[o].v,v);
if(l==r || tr[o].v.k==v.k || !v.id) return o;
double x = cross(tr[o].v,v);
if(x<l || x>r) return o;
if(v.k > tr[o].v.k){
int wtf = ins(ls,l,mid,v);
ls=wtf;
}
else{
int wtf = ins(rs,mid+1,r,v);
rs=wtf;
}
pushup(o);
return o;
}
int merge(int x, int y, int l, int r){
if(!x || !y) return x|y;
ins(x,l,r,tr[y].v);
int mid=l+r>>1;
int wtf = merge(tr[x].l, tr[y].l, l, mid); tr[x].l=wtf;
wtf = merge(tr[x].r, tr[y].r, mid+1, r); tr[x].r=wtf;
pushup(x);
return x;
}
inline int merge(int x, int y){
if(tr[x].siz<tr[y].siz) swap(x,y);
return merge(x,y,1,Lim);
}
ll query(int o, int l, int r, int x){
if(l==r) return tr[o].v.id ? tr[o].v.getY(x) : inf;
int mid=l+r>>1; ll ret;
if(x<=mid){
if(!ls) return tr[o].v.getY(x);
ret=query(ls,l,mid,x);
}
else{
if(!rs) return tr[o].v.getY(x);
ret=query(rs,mid+1,r,x);
}
return tr[o].v.id ? min(ret, tr[o].v.getY(x)) : ret;
}
#undef ls
#undef rs
}sgt;
inline void ins(int x){
int k=b[x]; ll b=dp[x]-(ll)lim*k;
rt[x] = sgt.ins(rt[x], 1, Lim, line(k,b,1));
}
inline ll query(int x){
return sgt.query(rt[x], 1, Lim, a[x]+lim);
}
void dfs(int u, int fa){
bool flag=0;
for(int i=0; i<g[u].size(); ++i){
int v=g[u][i];
if(v==fa) continue;
flag=1;
dfs(v,u);
rt[u] = sgt.merge(rt[u], rt[v]);
}
if(flag) dp[u] = query(u);
ins(u);
}
int main(){
//freopen("1.in","r",stdin);
//freopen("1.out","w",stdout);
sgt.tr.pb(LiChaoTree::Tree());
n=read();
for(int i=1; i<=n; ++i) a[i]=read();
for(int i=1; i<=n; ++i) b[i]=read();
int u,v;
for(int i=1; i<n; ++i){
u=read(), v=read();
g[u].pb(v), g[v].pb(u);
}
dfs(1,0);
for(int i=1; i<=n; ++i) printf("%lld ",dp[i]);
return 0;
}
总结一点:不少斜率优化题都是单点求最值,所以可以用李超树这个简单的数据结构维护。但李超树并不能动态维护凸包面积,所以像【HAOI2011 防线修建】这种题就只能用平衡树做。