NOIP普及组
加工零件
+++
题目描述
凯凯的工厂正在有条不紊地生产一种神奇的零件,神奇的零件的生产过程自然也很神奇。工厂里有 nn 位工人,工人们从 1 sim n1∼n 编号。某些工人之间存在双向的零件传送带。保证每两名工人之间最多只存在一条传送带。
如果 xx 号工人想生产一个被加工到第 L (L gt 1)L(L>1) 阶段的零件,则所有与 xx 号工人有传送带直接相连的工人,都需要生产一个被加工到第 L - 1L−1 阶段的零件(但 xx 号工人自己无需生产第 L - 1L−1 阶段的零件)。
如果 xx 号工人想生产一个被加工到第 1 阶段的零件,则所有与 xx 号工人有传送带直接相连的工人,都需要为 xx 号工人提供一个原材料。
轩轩是 1 号工人。现在给出 qq 张工单,第 ii 张工单表示编号为 a_ia**i 的工人想生产一个第 L_iL**i 阶段的零件。轩轩想知道对于每张工单,他是否需要给别人提供原材料。他知道聪明的你一定可以帮他计算出来!
输入格式
第一行三个正整数 nn,mm 和 qq,分别表示工人的数目、传送带的数目和工单的数目。
接下来 mm 行,每行两个正整数 uu 和 vv,表示编号为 uu 和 vv 的工人之间存在一条零件传输带。保证 u eq vu=v。
接下来 qq 行,每行两个正整数 aa 和 LL,表示编号为 aa 的工人想生产一个第 LL 阶段的零件。
输出格式
共 qq 行,每行一个字符串 Yes 或者 No。如果按照第 ii 张工单生产,需要编号为 1 的轩轩提供原材料,则在第 ii 行输出 Yes;否则在第 ii 行输出 No。注意输出不含引号。
输入输出样例
输入 #1复制
3 2 6
1 2
2 3
1 1
2 1
3 1
1 2
2 2
3 2
输出 #1复制
No
Yes
No
Yes
No
Yes
输入 #2复制
5 5 5
1 2
2 3
3 4
4 5
1 5
1 1
1 2
1 3
1 4
1 5
输出 #2复制
No
Yes
No
Yes
Yes
说明/提示
【输入输出样例 1 说明】
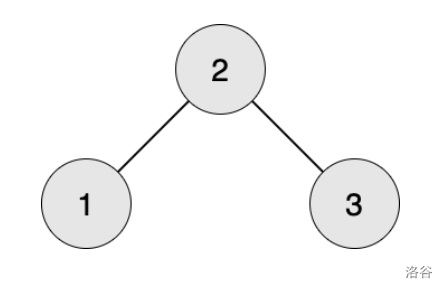
编号为 1 的工人想生产第 1 阶段的零件,需要编号为 2 的工人提供原材料。
编号为 2 的工人想生产第 1 阶段的零件,需要编号为 1 和 3 的工人提供原材料。
编号为 3 的工人想生产第 1 阶段的零件,需要编号为 2 的工人提供原材料。
编号为 1 的工人想生产第 2 阶段的零件,需要编号为 2 的工人生产第 1 阶段的零 件,需要编号为 1 和 3 的工人提供原材料。
编号为 2 的工人想生产第 2 阶段的零件,需要编号为 1 和 3 的工人生产第 1 阶段的零件,他/她们都需要编号为 2 的工人提供原材料。
编号为 3 的工人想生产第 2 阶段的零件,需要编号为 2 的工人生产第 1 阶段的零件,需要编号为 1 和 3 的工人提供原材料。
【输入输出样例 2 说明】
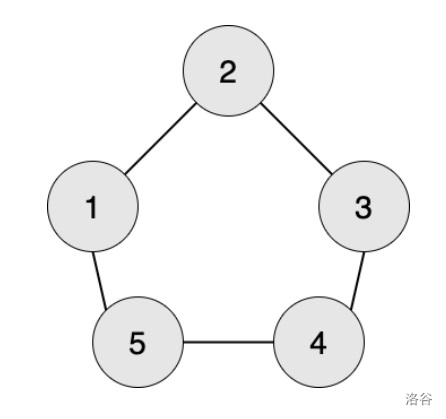
编号为 1 的工人想生产第 1 阶段的零件,需要编号为 2 和 5 的工人提供原材料。
编号为 1 的工人想生产第 2 阶段的零件,需要编号为 2 和 5 的工人生产第 1 阶段的零件,需要编号为 1,3,41,3,4 的工人提供原材料。
编号为 1 的工人想生产第 3 阶段的零件,需要编号为 2 和 5 的工人生产第 2 阶段的零件,需要编号为 1,3,41,3,4 的工人生产第 1 阶段的零件,需要编号为 2,3,4,52,3,4,5 的工人提供原材料。
编号为 1 的工人想生产第 4 阶段的零件,需要编号为 2 和 5 的工人生产第 3 阶段的零件,需要编号为 1,3,41,3,4 的工人生产第 2 阶段的零件,需要编号为 2,3,4,52,3,4,5 的工人生产第 1 阶段的零件,需要全部工人提供原材料。
编号为 1 的工人想生产第 5 阶段的零件,需要编号为 2 和 5 的工人生产第 4 阶段的零件,需要编号为 1,3,41,3,4 的工人生产第 3 阶段的零件,需要编号为 2,3,4,52,3,4,5 的工人生产第 2 阶段的零件,需要全部工人生产第 1 阶段的零件,需要全部工人提供原材料。
+++
题解
我们可以知道,无向图中如果有a点到b点距离为L的情况,就可以通过来回通过一条无向边构造出距离为L + 2,L + 4 ,..., L + n(n为偶数) 的方案。因此本题可换一种思路,即询问是否存在一种方案,线路长度和L的奇偶性相同的同时L大于等于此距离。转化为最短路问题。
运动dp中的状态机模型,我们可以把一个点分离成奇点和偶点,一条边分离成两条边,即1号点的偶点连接2号点的奇点,1号点的奇点连接2号店的偶点,最后bfs一遍求最短路即可。
最后不要忘记特判一下1号点是孤立结点的情况。
AC代码实现
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
const int N = 100010;
int h[N], e[N * 2], ne[N * 2], idx;
int dist[N][2];
int n, m, query;
PII q[N * 2];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void bfs()
{
memset(dist, 0x3f, sizeof dist);
int hh = 0, tt = 0;
q[0] = {1, 0};
dist[1][0] = 0;
while (hh <= tt)
{
PII t = q[hh ++ ];
int ver = t.first, type = t.second;
for (int i = h[ver]; i != -1; i = ne[i])
{
int j = e[i];
if(dist[j][type ^ 1] > dist[ver][type] + 1) //^相同为0,不同为1
{
dist[j][type ^ 1] = dist[ver][type] + 1;
q[ ++ tt ] = {j, type ^ 1};
}
}
}
}
int main()
{
scanf("%d%d%d", &n, &m, &query);
memset(h, -1, sizeof h);
while (m -- )
{
int u, v;
scanf("%d%d", &u, &v);
add(u, v), add(v, u);
}
bfs();
while (query -- )
{
int a, L;
scanf("%d%d", &a, &L);
if (a == 1 && h[a] == -1) puts("No");
else if (dist[a][L & 1] <= L) puts("Yes");
else puts("No");
}
return 0;
}