转:https://www.cnblogs.com/JVxie/p/4859889.html
堆是利用完全二叉树的结构来维护一组数据,然后进行相关操作,一般的操作进行一次的时间复杂度在 O(1) ~ O(logn) 之间。
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。我们知道二叉树可以用数组模拟,堆自然也可以。
现在让我们来画一棵完全二叉树:
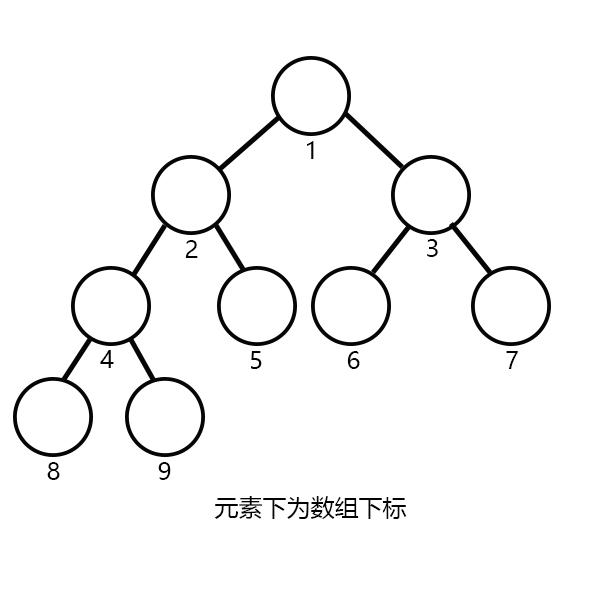
从图中可以看出,元素的父亲节点数组下标是本身的1/2(只取整数部分),所以我们很容易去模拟,也很容易证明其所有操作都为log级别~~
堆还分为两种类型:大根堆、小根堆
顾名思义,就是保证根节点是所有数据中最大/小,并且尽力让小/大的节点在上方
不过有一点需要注意:堆内的元素并不一定数组下标顺序来排序的!!
很多的初学者会错误的认为大/小根堆中
下标为1就是第一大/小,2是第二大/小……
原因会在后面解释,现在你只需要深深地记住这一点!
我们刚刚画的完全二叉树中并没有任何元素,现在让我们加入一组数据吧!
下标从1到9分别加入:{8,5,2,9,3,7,1,4,6}。
如下图所示
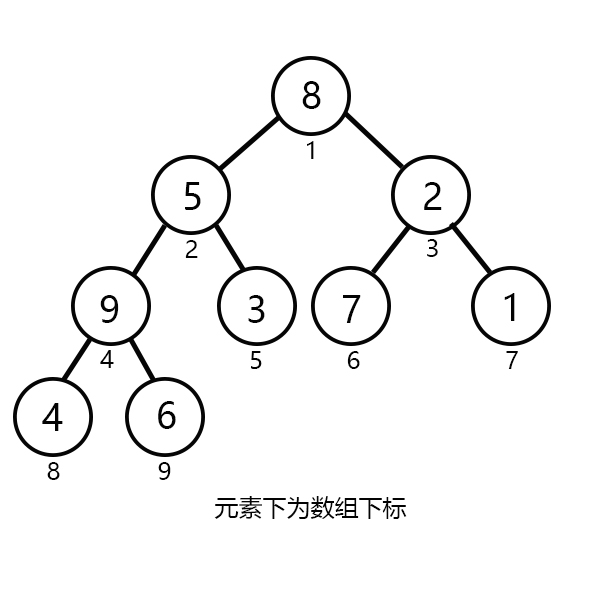
我们可以发现这组数据是杂乱无章的,我们该如何去维护呢?
现在我就来介绍一下堆的几个基本操作:
- 上浮 shift_up
- 下沉 shift_down
- 插入 push
- 弹出 pop
- 取顶 top
- 堆排序 heap_sort
那么我们开始讲解操作过程吧,我们以小根堆为例
刚刚那组未处理过的数据中我们很容易就能看出,根节点1元素8绝对不是最小的
我们很容易发现它的一个儿子节点3(元素2)比它来的小,我们怎么将它放到最高点呢?很简单,直接交换嘛~~
但是,我们又发现了,3的一个儿子节点7(元素1)似乎更适合在根节点。
这时候我们是无法直接和根节点交换的,那我们就需要一个操作来实现这个交换过程,那就是上浮 shift_up。
操作过程如下:
从当前结点开始,和它的父亲节点比较,若是比父亲节点来的小,就交换,
然后将当前询问的节点下标更新为原父亲节点下标;否则退出。
模拟操作图示:
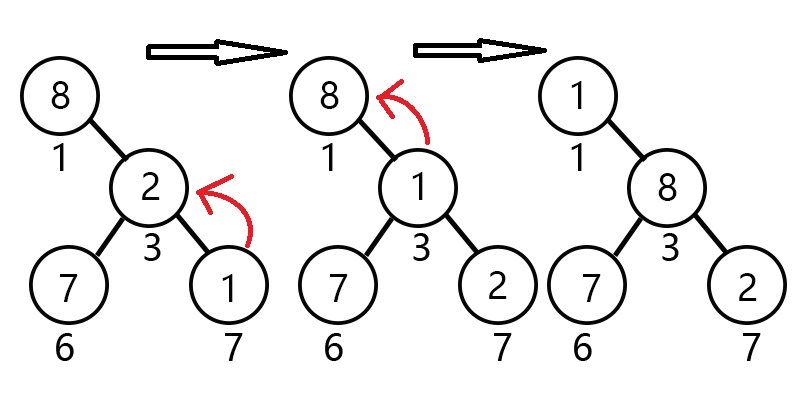
伪代码如下:
Shift_up( i )
{
while( i / 2 >= 1)
{
if( 堆数组名[ i ] < 堆数组名[ i/2 ] )
{
swap( 堆数组名[ i ] , 堆数组名[ i/2 ]) ;
i = i / 2;
}
else break;
}
这一次上浮完毕之后呢,我们又发现了一个问题,貌似节点3(元素8)不太合适放在那,而它的子节点7(元素2)好像才应该在那个位置
我们知道,小根堆是尽力要让小的元素在较上方的节点,而下沉与上浮一样要以交换来不断操作,所以我们应该让节点7与其交换。
由此我们可以得出下沉的算法了:
让当前结点的左右儿子(如果有的话)作比较,哪个比较小就和它交换,并更新询问节点的下标为被交换的儿子节点下标,否则退出。
模拟操作图示:
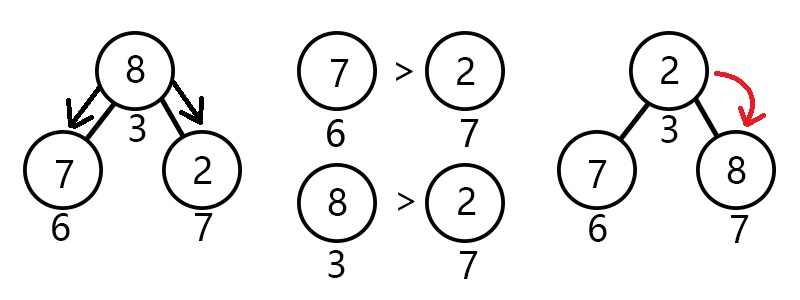
伪代码如下:
Shift_down( i , n ) //n表示当前有n个节点
{
while( i * 2 <= n)
{
T = i * 2 ;
if( T + 1 <= n && 堆数组名[ T + 1 ] < 堆数组名[ T ])
T++;
if( 堆数组名[ i ] < 堆数组名[ T ] )
{
swap( 堆数组名[ i ] , 堆数组名[ T ] );
i = T;
}
else break;
}
// 伪代码下沉函数 第二个if判断有错误吧
讲完了上浮和下沉,接下来就是插入操作了~~~~
我们前面用的插入是直接插入,所以数据才会杂乱无章,那么我们如何在插入的时候边维护堆呢?
其实很简单,每次插入的时候呢,我们都往最后一个插入,让后使它上浮。
伪代码如下:
Push ( x )
{
n++;
堆数组名[ n ] = x;
Shift_up( n );
}
咳咳,说完了插入,我们总需要会弹出吧~~~~~
弹出,顾名思义就是把顶元素弹掉,但是,弹掉以后不是群龙无首吗??
我们如何去维护这堆数据呢?
稍加思考,我们不难得出一个十分巧妙的算法:
让根节点元素和尾节点进行交换,然后让现在的根元素下沉就可以了!
伪代码如下:
Pop ( x )
{
swap( 堆数组名[1] , 堆数组名[ n ] );
n--;
Shift_down( 1 );
}
接下来是取顶…..根节点数组下标必定是1,返回堆[ 1 ]就OK了~~
注意:每次取顶要判断堆内是否有元素
说完这些,我们再来说说堆排序。
之前说过堆是无法以数组下标的顺序来来排序的对吧?
所以我个人认为呢,并不存在堆排序这样的操作,即便网上有很多堆排序的算法,但是我这里有个更加方便的算法:
开一个新的数组,每次取堆顶元素放进去,然后弹掉堆顶就OK了~
伪代码如下:
Heap_sort( a[] )
{
k=0;
while( size > 0 )
{
k++;
a[ k ] = top();
pop();
}
}
堆排序的时间复杂度是O(nlogn)理论上是十分稳定的,但是对于我们来说并没有什么卵用。
我们要排序的话,直接使用快排即可,时间更快,用堆排还需要O(2*n)的空间。这也是为什么我说堆的操作
时间复杂度在O(1)~O(logn)。
讲完到这里,堆也基本介绍完了,那么它有什么用呢??
举个例子,比如当我们每次都要取某一些元素的最小值,而取出来操作后要再放回去,重复做这样的事情。
我们若是用快排的话,最坏的情况需要O(q*n^2),而若是堆,仅需要O(q*logn),时间复杂度瞬间低了不少。
还有一种最短路算法——Dijkstra,需要用到堆来优化
最后附上作者写的一份堆操作的代码(C++):
1 #include<cstdio>
2 #include<cstring>
3 #include<iostream>
4 #include<algorithm>
5 #define maxn 100010 //这部分可以自己定义堆内存多少个元素
6 using namespace std;
7 struct Heap
8 {
9 int size,queue[maxn];
10 Heap() //初始化
11 {
12 size=0;
13 for(int i=0;i<maxn;i++)
14 queue[i]=0;
15 }
16 void shift_up(int i) //上浮
17 {
18 while(i>1)
19 {
20 if(queue[i]<queue[i>>1])
21 {
22 int temp=queue[i];
23 queue[i]=queue[i>>1];
24 queue[i>>1]=temp;
25 }
26 i>>=1;
27 }
28 }
29 void shift_down(int i) //下沉
30 {
31 while((i<<1)<=size)
32 {
33 int next=i<<1;
34 if(next<size && queue[next+1]<queue[next])
35 next++;
36 if(queue[i]>queue[next])
37 {
38 int temp=queue[i];
39 queue[i]=queue[next];
40 queue[next]=temp;
41 i=next;
42 }
43 else return ;
44 }
45 }
46 void push(int x) //加入元素
47 {
48 queue[++size]=x;
49 shift_up(size);
50 }
51 void pop() //弹出操作
52 {
53 int temp=queue[1];
54 queue[1]=queue[size];
55 queue[size]=temp;
56 size--;
57 shift_down(1);
58 }
59 int top(){return queue[1];}
60 bool empty(){return size;}
61 void heap_sort() //另一种堆排方式,由于难以证明其正确性
62 { //我就没有在博客里介绍了,可以自己测试
63 int m=size;
64 for(int i=1;i<=size;i++)
65 {
66 int temp=queue[m];
67 queue[m]=queue[i];
68 queue[i]=temp;
69 m--;
70 shift_down(i);
71 }
72 }
73 };
74 int main()
75 {
76 Heap Q;
77 int n,a,i,j,k;
78 cin>>n;
79 for(i=1;i<=n;i++)
80 {
81 cin>>a;
82 Q.push(a); //放入堆内
83 }
84
85 for(i=1;i<=n;i++)
86 {
87 cout<<Q.top()<<" "; //输出堆顶元素
88 Q.pop(); //弹出堆顶元素
89 }
90 return