转自:https://blog.csdn.net/shuangde800
关键思想:
依据哈弗曼树的定义,一棵二叉树要使其WPL值最小,必须使权值越大的叶子结点越靠近根结点,而权值越小的叶子结点越远离根结点。
哈弗曼根据这一特点提出了一种构造最优二叉树的方法,其基本思想如下:
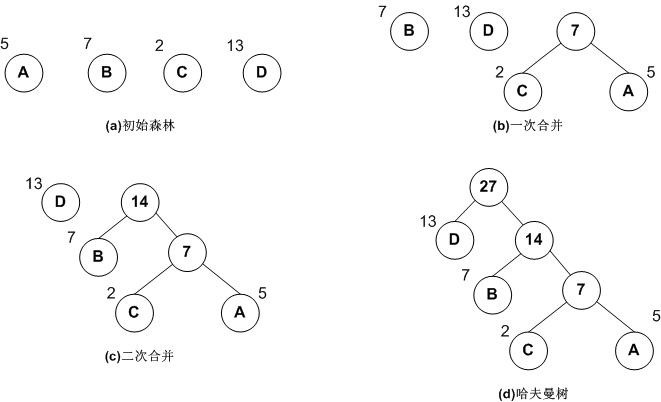
1。根据给定的n个权值{w1, w2, w3 ... wn },构造n棵只有根节点的二叉树,令起权值为wj
2。在森林中选取两棵根节点权值最小的树作为左右子树,构造一颗新的二叉树,置新二叉树根节点权值为其左右子树根节点权值之和。注意,左子树的权值应小于右子树的权值。
3。从森林中删除这两棵树,同时将新得到的二叉树加入森林中。(换句话说,之前的2棵最小的根节点已经被合并成一个新的结点了)
4。重复上述两步,直到只含一棵树为止,这棵树即是 哈弗曼树
以下演示了用Huffman算法构造一棵Huffman树的过程:
考研题目:

三、哈夫曼树的在编码中的应用
在电文传输中,须要将电文中出现的每一个字符进行二进制编码。在设计编码时须要遵守两个原则:
(1)发送方传输的二进制编码,到接收方解码后必须具有唯一性,即解码结果与发送方发送的电文全然一样;
(2)发送的二进制编码尽可能地短。以下我们介绍两种编码的方式。
1. 等长编码
这样的编码方式的特点是每一个字符的编码长度同样(编码长度就是每一个编码所含的二进制位数)。如果字符集仅仅含有4个字符A,B,C,D,用二进制两位表示的编码分别为00,01,10,11。若如今有一段电文为:ABACCDA,则应发送二进制序列:00010010101100,总长度为14位。当接收方接收到这段电文后,将按两位一段进行译码。这样的编码的特点是译码简单且具有唯一性,但编码长度并非最短的。
2. 不等长编码
在传送电文时,为了使其二进制位数尽可能地少,能够将每一个字符的编码设计为不等长的,使用频度较高的字符分配一个相对照较短的编码,使用频度较低的字符分配一个比較长的编码。比如,能够为A,B,C,D四个字符分别分配0,00,1,01,并可将上述电文用二进制序列:000011010发送,其长度仅仅有9个二进制位,但随之带来了一个问题,接收方接到这段电文后无法进行译码,由于无法断定前面4个0是4个A,1个B、2个A,还是2个B,即译码不唯一,因此这样的编码方法不可使用。
因此,为了设计长短不等的编码,以便降低电文的总长,还必须考虑编码的唯一性:即在建立不等长编码时必须使不论什么一个字符的编码都不是还有一个字符的前缀,这宗编码称为前缀编码(prefix code)
(1)利用字符集中每一个字符的使用频率作为权值构造一个哈夫曼树;
(2)从根结点開始,为到每一个叶子结点路径上的左分支赋予0,右分支赋予1,并从根到叶子方向形成该叶子结点的编码
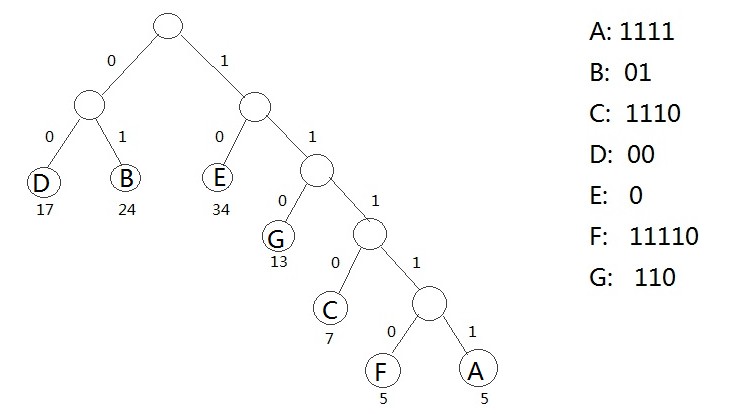
例题:
如果一个文本文件TFile中仅仅包括7个字符{A,B,C,D,E,F,G},这7个字符在文本中出现的次数为{5,24,7,17,34,5,13}
利用哈夫曼树能够为文件TFile构造出符合前缀编码要求的不等长编码
详细做法:
1. 将TFile中7个字符都作为叶子结点,每一个字符出现次数作为该叶子结点的权值
2. 规定哈夫曼树中全部左分支表示字符0,全部右分支表示字符1,将依次从根结点到每一个叶子结点所经过的分支的二进制位的序列作为该
结点相应的字符编码
3. 因为从根结点到不论什么一个叶子结点都不可能经过其它叶子,这样的编码一定是前缀编码,哈夫曼树的带权路径长度正好是文件TFile编码
的总长度
通过哈夫曼树来构造的编码称为哈弗曼编码(huffman code)
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define N 10 // 带编码字符的个数,即树中叶结点的最大个数
#define M (2*N-1) // 树中总的结点数目
class HTNode{ // 树中结点的结构
public:
unsigned int weight;
unsigned int parent,lchild,rchild;
};
class HTCode{
public:
char data; // 待编码的字符
int weight; // 字符的权值
char code[N]; // 字符的编码
};
void Init(HTCode hc[], int *n){
// 初始化,读入待编码字符的个数n,从键盘输入n个字符和n个权值
int i;
printf("input n = ");
scanf("%d",&(*n));
printf("
input %d character
",*n);
fflush(stdin);
for(i=1; i<=*n; ++i)
scanf("%c",&hc[i].data);
printf("
input %d weight
",*n);
for(i=1; i<=*n; ++i)
scanf("%d",&(hc[i].weight) );
fflush(stdin);
}//
void Select(HTNode ht[], int k, int *s1, int *s2){
// ht[1...k]中选择parent为0,而且weight最小的两个结点,其序号由指针变量s1,s2指示
int i;
for(i=1; i<=k && ht[i].parent != 0; ++i){
; ;
}
*s1 = i;
for(i=1; i<=k; ++i){
if(ht[i].parent==0 && ht[i].weight<ht[*s1].weight)
*s1 = i;
}
for(i=1; i<=k; ++i){
if(ht[i].parent==0 && i!=*s1)
break;
}
*s2 = i;
for(i=1; i<=k; ++i){
if(ht[i].parent==0 && i!=*s1 && ht[i].weight<ht[*s2].weight)
*s2 = i;
}
}
void HuffmanCoding(HTNode ht[],HTCode hc[],int n){
// 构造Huffman树ht,并求出n个字符的编码
char cd[N];
int i,j,m,c,f,s1,s2,start;
m = 2*n-1;
for(i=1; i<=m; ++i){
if(i <= n)
ht[i].weight = hc[i].weight;
else
ht[i].parent = 0;
ht[i].parent = ht[i].lchild = ht[i].rchild = 0;
}
for(i=n+1; i<=m; ++i){
Select(ht, i-1, &s1, &s2);
ht[s1].parent = i;
ht[s2].parent = i;
ht[i].lchild = s1;
ht[i].rchild = s2;
ht[i].weight = ht[s1].weight+ht[s2].weight;
}
cd[n-1] = '�';
for(i=1; i<=n; ++i){
start = n-1;
for(c=i,f=ht[i].parent; f; c=f,f=ht[f].parent){
if(ht[f].lchild == c)
cd[--start] = '0';
else
cd[--start] = '1';
}
strcpy(hc[i].code, &cd[start]);
}
}
int main()
{
int i,m,n,w[N+1];
HTNode ht[M+1];
HTCode hc[N+1];
Init(hc, &n); // 初始化
HuffmanCoding(ht,hc,n); // 构造Huffman树,并形成字符的编码
for(i=1; i<=n; ++i)
printf("
%c---%s",hc[i].data,hc[i].code);
printf("
");
return 0;
}
