图的定义:
图在数据结构中是中一对多的关系,一般分为无向图与无向图
常用 邻接矩阵 或者 邻接链表 来表示图中结点的关系
⑴图是由顶点集V和顶点间的关系集合E(边的集合)组成的一种数据结构
⑵用二元组定义为:G=(V,E)。
例如:
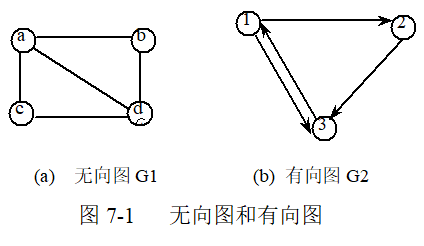
对于图7-1所示的无向图G1和有向图G2,它们的数据结构可以描述为:
G1=(V1,E1), 其中 V1={a,b,c,d},E1={(a,b),(a,c),(a,d),(b,d),(c,d)},
G2=(V2,E2),其中 V2={1,2,3}, E2={<1,2>,<1,3>,<2,3>,<3,1>}。
有向图与无向图
⑴在图中,若用箭头标明了边是有方向性的,则称这样的图为有向图,否则称为无向图。
如图7-1中:
①G1为无向图, ②G2 为有向图。
⑵在无向图中:一条边(x,y)与(y,x)表示的结果相同,用圆括号表示,
⑶在有向图中:一条边<x,y>与<y,x>表示的结果不相同,故用尖括号表示。<x,y>表示从顶点x发向顶点y的边,x为始点,y为终点。
⑷有向边也称为弧,x为弧尾,y为弧头,则<x,y>表示为一条弧, 而<y,x>表示y为弧尾,x为弧头的另一条弧 。
完全图/稠密图/稀疏图:
⑴具有n个顶点,n(n-1)/2条边的图,称为完全无向图,
⑵具有n个顶点,n(n-1) 条弧的有向图,称为完全有向图。
⑶完全无向图和完全有向图都称为完全图。
⑷对于一般无向图,顶点数为n,边数为e,则 0≤e ≤n(n-1)/2。
⑸对于一般有向图,顶点数为n,弧数为e, 则 0≤e≤n(n-1) 。
⑹当一个图接近完全图时,则称它为稠密图,
⑺当一个图中含有较少的边或弧时,则称它为稀疏图。
度/出度/入度:
⑴在图中,一个顶点依附的边或弧的数目,称为该顶点的度。
⑵在有向图中,一个顶点依附的弧头数目,称为该顶点的入度。
⑶一个顶点依附的弧尾数目,称为该顶点的出度,某个顶点的入度和出度之和称为该顶点的度。
⑷若图中有n个顶点,e条边或弧,第i个顶点的度为di,则有 e=1/2 * Σ(1<= i <= n, di)
子图
⑴若有两个图G1和G2, G1=(V1,E1), G2=(V2,E2), 满足如下条件:
V2⊆V1 ,E2⊆ E1,即V2为V1的子集,E2为E1的子集,则 称图G2为图G1的子图。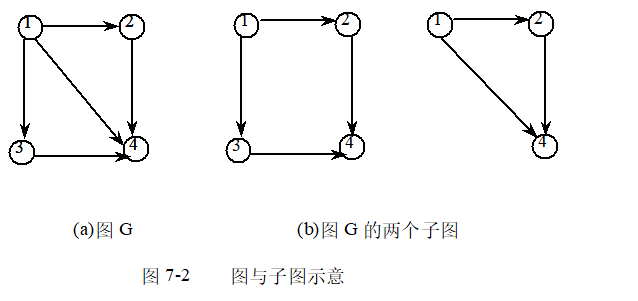
权:
⑴在图的边或弧中给出相关的数,称为权。
⑵权可以代表一个顶点到另一个顶点的距离,耗费
等,带权图一般称为网。
一个图由多个结点以及边组成。
无向图例子:
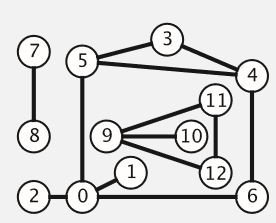
有向图例子:
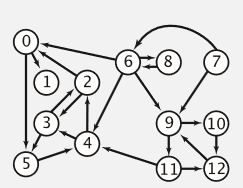
从上述例子中可以看出,一个图表是由数个顶点和边组成的。
其中,无向图的边是没方向的,即两个相连的顶点可以互相抵达。
而有向图的边是有方向的,即两个相连的顶点,根据边的方向,只能由一个顶点通向另一个顶点。(当然,如有向图例子中的2和3,由于有两个指向对方的方向,所以2和3是互通的。)
