描述
将8个皇后放在8*8的棋盘上,要求这8个皇后两两不能在同一水平、垂直或对角线上,求所有放置方法。
求解
这是一道经典的递归问题(当然也可以暴力枚举,但不够雅观简洁),8*8的棋盘递归后转变为7*7的棋盘来解决,7*7的棋盘递归后转变为6*6的棋盘来解决,……,但这里的问题是前面的放置会影响后面的放置情况,所以还需要一个记录放置状态的全局变量;后面的放置不成功还会回溯到前面的情况重新放置,所以还要分不同的情况来回溯。
作为一道递归题,当然只需要解决两部分即可:终止条件和递归核心。
终止条件
终止条件只有一个,即已经填完所有的8皇后,显然返回就行了。
递归核心
枚举当前行内所有点,如果能成功放置,则放置,并调用下一层递归;如果不能,则自继续枚举该行的下一个点。
判断放置成功的条件为:
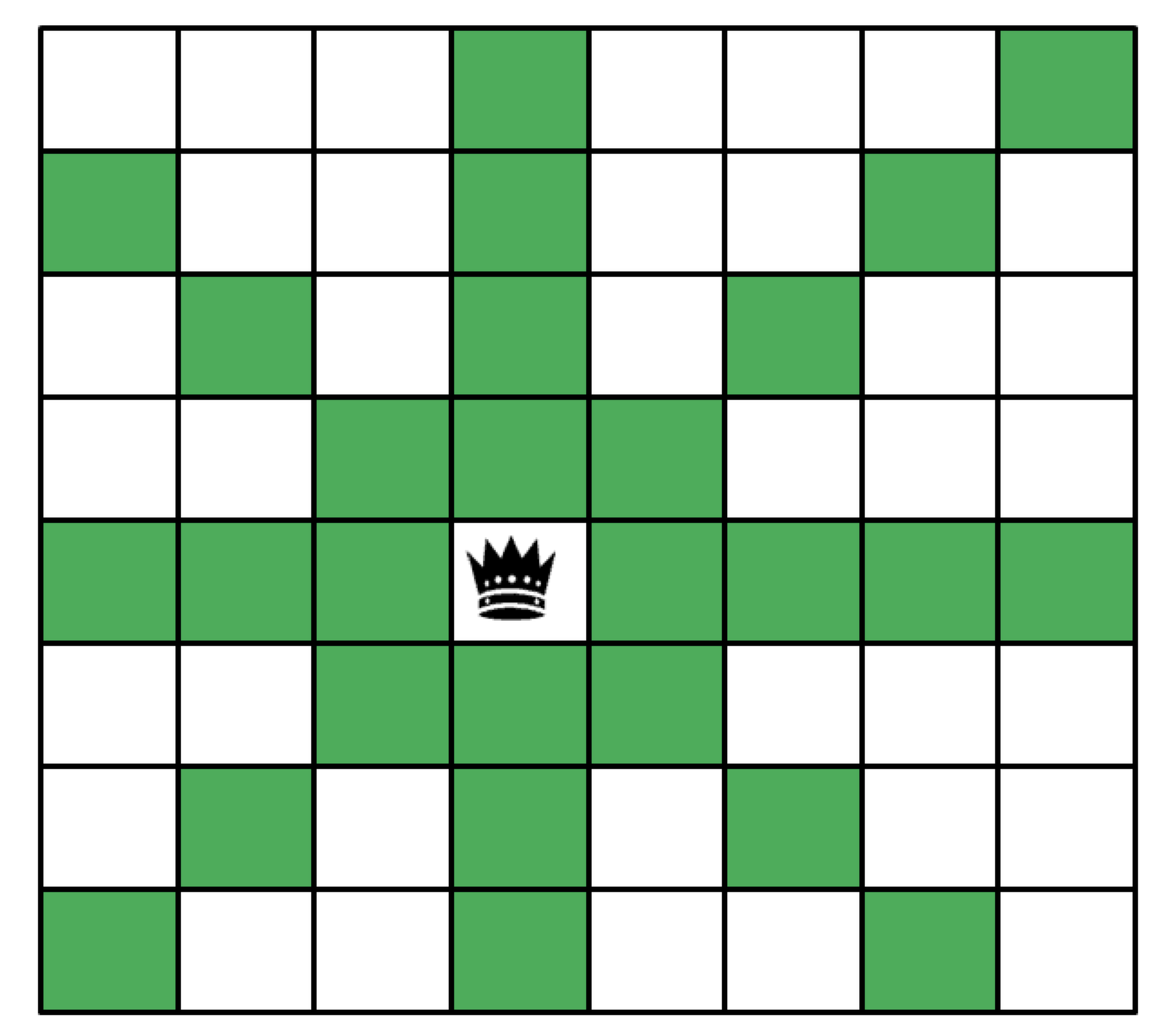
在水平、垂直线上都比较容易判断,关键是在对角线上的判断为:设两个点为(x1, y1), (x2, y2),则两个点在对角线上应满足(斜率是±1)两条直线方程:x1 + y1 = x2 + y2 (主对角线),x1 - y1 = x2 - y2(副对角线)。
数据结构
由于每一行只能放置一个皇后,所以只需要用一个一位数组记录即可,第i行放置了第j列的皇后,记为a[i] = j,这样空间复杂度从O(n²)变为O(n)
代码
用Python递归版的代码可以非常简洁:
num_queen = 8 count = 0 queen_col = [0] * num_queen def recursion(cur_row = 0): global num_queen global queen_col global count # stop condition if cur_row == num_queen: count += 1 print(queen_col) return # main recursion process for i in range(num_queen): queen_col[cur_row] = i flag = True # check if the current point is available # only check the row before the current row for j in range(cur_row): x1 = j y1 = queen_col[j] x2 = cur_row y2 = queen_col[cur_row] if y1 == y2 or x1+y1 == x2+y2 or y1-x1 == y2-x2: flag = False break if flag: recursion(cur_row+1) recursion() print(count)
输出共92种方法