首先,为啥会要讨论这个问题。
我得为昨天拖了小组后腿深表歉意。其实程序逻辑很快就理通了的,但自己总是会因为各种各样的小问题束缚手脚,看接下来这个图片:
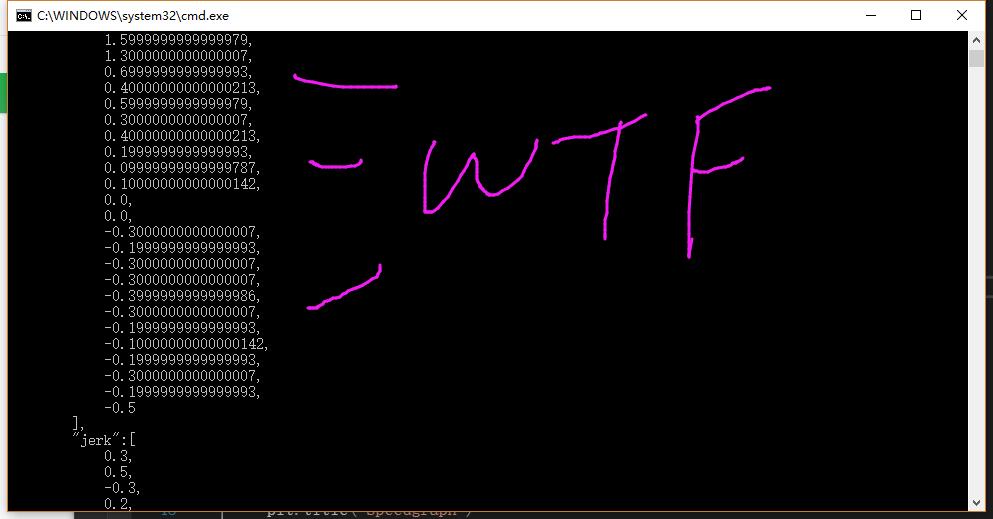
稍微有数据敏感性的同学就能看出,中间这么一大堆又是0000又是999还是这么多位的小数,一看就是异常数据。这块数据的产生,源于代码里对两个字符串做了float转换并相减,导致出现了这种数据异常的错误。那么问题来了,1.这种异常是如何产生的?2.有哪些方法可以解决这种问题呢?3.编程中间还有哪些与这个问题相关的注意事项呢?
第一部分:这种异常是如何产生的呢?
我们先来看演示:
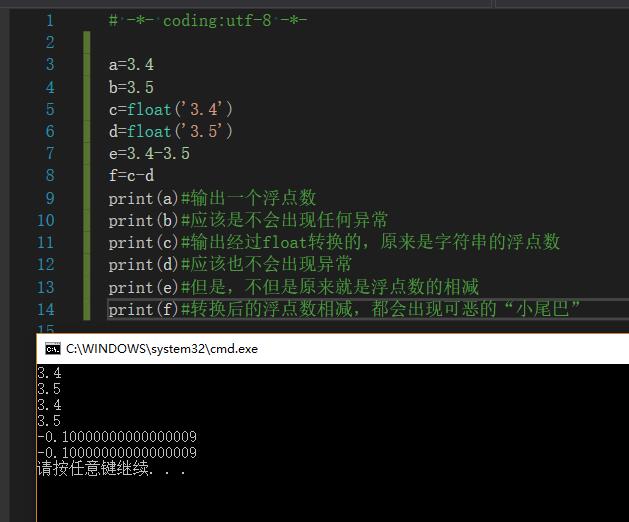
看来,直接输出float型数据,以及对字符串进行的float转换,本身并没有什么问题,那么为什么浮点数相减就会出现这个可恶的小尾巴呢?我们有必要从计算机本身数字加减的机制进行探究。有学习过《计算机组成原理》等基本课程、哪怕只是简单了解计算机内部运行机制的同学都明白,计算机内部的加减乘除都是要把数字转化成为二进制实现的。那么,我们此处的浮点数,也要转换为二进制,才能进行计算。Python内浮点数是用机器上浮点数的本机双精度(64 bit)表示的。提供大约17位的精度和范围从-308到308的指数。和C语言里面的double类型相同【可参考C语言double类型的解释】。
我们来看一个简单的例子。十进制1.1转换成二进制是什么数?十进制整数部分转化成二进制,用短除法处以2倒序取余。小数部分转化为二进制是用乘法乘2正序取整。见下面一个浮点数转二进制数的例子。
1.10整数部分就是1,转换成二进制1(这里整数转二进制不再赘述)
小数部分:0.1
0.1*2=0.2取整数部分0,基数=0.2
0.2*2=0.4取整数部分0,基数=0.4
0.4*2=0.8取整数部分0,基数=0.8
0.8*2=1.6取整数部分1,基数=1.6-1=0.6
0.6*2=1.2取整数部分1,基数=1.2-1=0.2
0.2*2=0.4取整数部分0,基数=0.4
.
.
.
直至基数为0。1.1用二进制表示为:1.000110...xxxx....(后面表示省略)
关于之前的演示,相当于,因为3.4的存储,发生了精度损失(3.5不会,因为3.5的二进制是11.1,补码存储依然不会发生精度损失),所以在相减的时候,发生了一次精度损失,最后结果存储的时候,再次发生一次精度损失。所以,才会出现最后的小尾巴情况。
第二部分:有哪些方法可以解决这个问题呢?
解决这个问题?不存在的,除非是提高精度——让计算机内能够完整的存储数字的二进制(二进制补码)表示,否则的话,只要有精度损失,就指不定什么时候会冒出来小尾巴。我们追求的解决,自然也是从提高精度,和“表面看起来正确”这两条道路去追求。
提高精度——Python本身自带的float已经是可支持浮点数的最高精度形式。当然,这个肯定是不能阻挡我们对更高精度的要求,这里可以自己实现高精度的数据形式,也可以使用Python扩展模块:Decimal。使用Decimal本身需要导入decimal包,初始化decimal数据可以使用整型数据和字符串,而不能使用float型数据,正如之前我们所说的那样,某些浮点数存储会发生精度损失——这意味着float本身就不够精确。
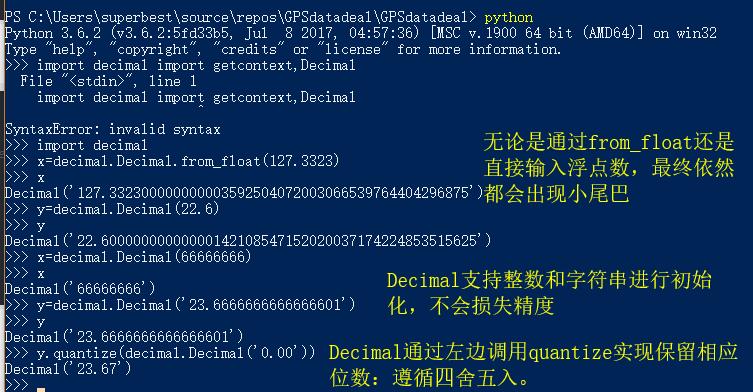
当然,还有很多抖机灵的方法,比如说结果转换成字符串然后再截取?!
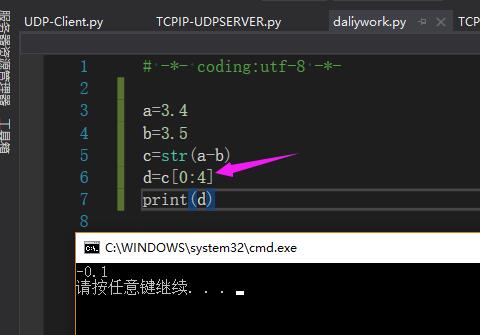
你可能体会不到,这个是一种针对数据波动范围相对确定,相当实用的方法——虽然应该没有任何一个脑子正常的程序员会推崇这种方法。这种方法就是追求的“表面上看起来正确”,你看,最后的显示出来的结果不就是-0.1么?
自然,还有print的%精度控制,这里就不赘述。而且也不想详述这个,毕竟这个惊为天人的字符串截取方法,都还是对字符串进行了处理,而%精度控制只是显示的时候做了处理,可真是够“表面”的。
不得不说,也是受这种方法的启发,本人使用的方法,是利用Python int转换“舍去小数点后所有数字”的特点,把原浮点数乘以需要保留精度的位数,然后转换成整数,再除回去,这样就形成了“表面正确”的数据,效果不要太好。
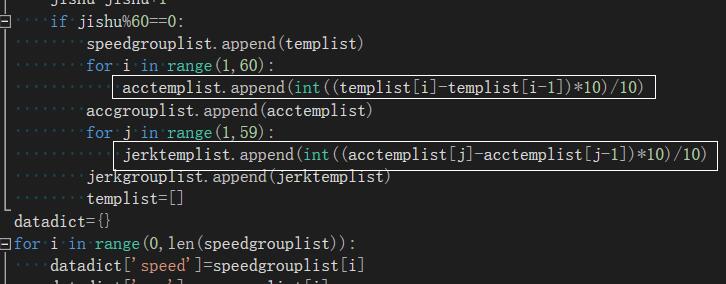
总结一下!解决这个精度损失带来的“恶魔小尾巴”问题,我们大体上有提高数据格式精度和只追求最终显示改变两大思路。
提高数据格式精度:使用扩展包decimal
只追求最终显示改变:printf %精度控制 ,字符串截取指定位数,先移动小数点、转换成整型舍去末尾、再把小数点移动回来。等方法。
第三部分:编程中间还有哪些和这个问题相关的注意事项呢?
这个小尾巴让我可谓一开始是焦头烂额,也严重耽误了小组研究进度。通过我们之前的探究,可以发现,浮点数本身表示由于受计算机限制,经常是不精确的。所以,日常数据中,最好不要用浮点数。
可能有些人觉得精度损失一些没有什么,然而浮点数的精度损失关键时候可不只只是精度损失,甚至会影响流程控制!浮点数不只有Python里面有,咱们用更加基本的C++来说明这个问题:
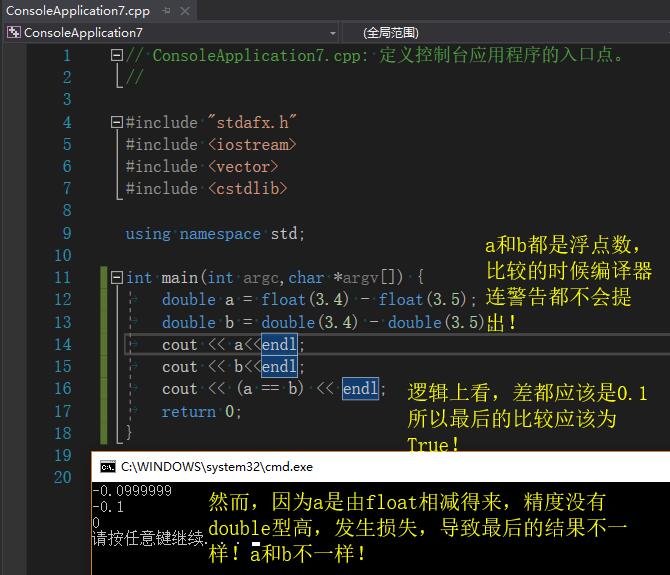
当精度损失已经让程序的走向开始不符合逻辑的时候,你还会轻视这个问题么?
这里给广大同仁们分享一篇专门讲解浮点数的文章,深入了解,真的有很多可圈可点之处!