一、杂波和回波信号的频谱特性
1、雷达回波信号的频谱
回波信号:
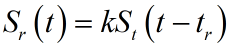 (1)
(1)
回波信号的频谱:
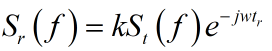 (2)
(2)
假设为固定目标;tr是一个固定的值。
分析频谱时首先分析幅频特性,对2式取模可得
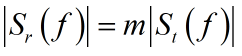
其中
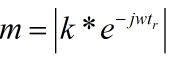
m为常数,可以看出,回波信号的幅频特性和发射信号的幅频特性相同。
当目标运动时。只需要在固定目标的基础上考虑上多普勒频率。
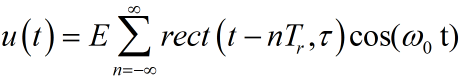
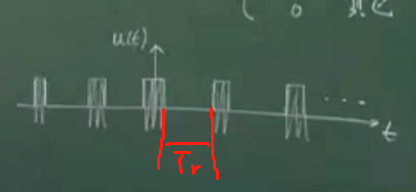
假设
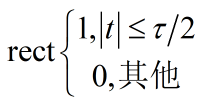

一个周期性的门函数。周期性的门函数的傅里叶变换(分析周期化函数时,通过傅里叶级数来进行分析的,由傅里叶级数可以知道,周期性信号的傅里叶变换是一个离散谱)。
负无穷到正无穷周期性函数的傅里叶函数是一个个δ函数。δ函数之间的间隔就是周期的倒数。在不包含载频的条件下,周期性门函数的傅里叶变换,肯定是一个个的δ函数,δ函数的间隔是Tr分之一。
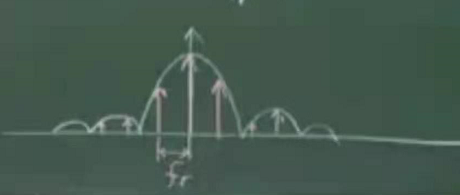
当乘以cos函数后,傅里叶变换的结果为。
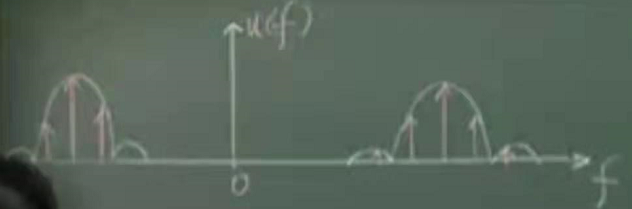
但在实际情况中,雷达信号应该是接收信号和天线扫描函数。

一般传统的天线扫描函数为高斯型。

所以求得的雷达信号的傅里叶变换为:

当没有多普勒频域时,发射信号的频谱和接收信号的频谱是一样的只是幅度大小不一样。
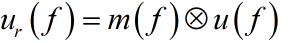
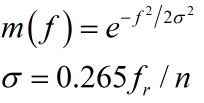
n表示的就是天线扫描期间收到的回波信号的脉冲个数。

由于任何函数和δ函数的卷积都是该函数本身,所以上边卷积得到的结果为(对于运动目标需要加一个多普勒频率);
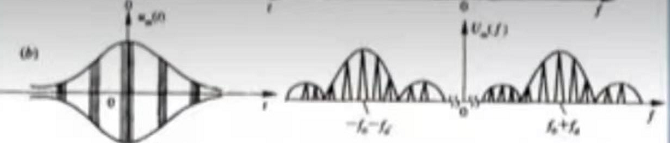
2、杂波频谱

杂波的频谱和m(f)的频谱相类似,因为杂波信号也要经过天线方向图函数。
二、动目标显示滤波器

相消器图
运用Z变换,迟延一个时间(采样周期),用Z变换描述为Z-1和不迟延的信号进行相加减。输入的是X(Z),输出的是Y(Z)。所以这个线性系统的Z变换为:
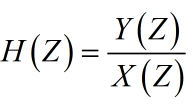
对Z变换进行处理得到这个线性系统的幅频特性。

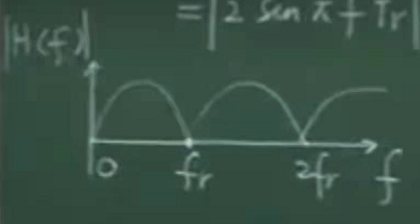
这个线性系统把频率为nfr,n为整数。回波滤除,当频率为0时,对应的是固定的目标,当频率不为0时,对应的目标是以盲速运动的目标。