第三章,逻辑回归(分类)and正则化
- 上半部分:逻辑回归
假设函数: ![]() (可以通过增加多项式来拟合曲线)
(可以通过增加多项式来拟合曲线)
要求:![]()
重新定义函数为: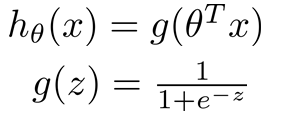
g(z)图像: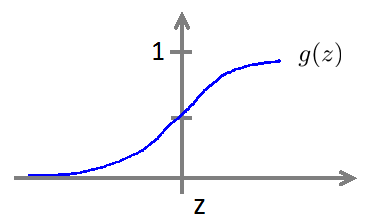

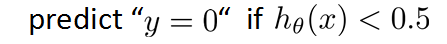
新的代价函数: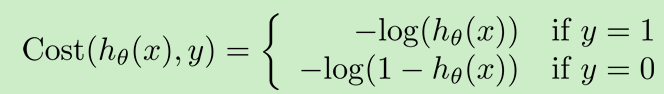
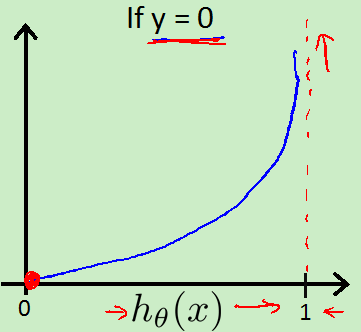
图像: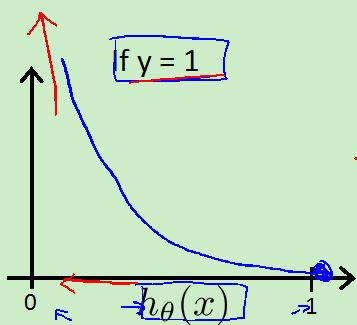
合并: 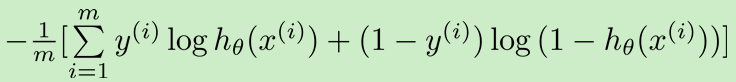

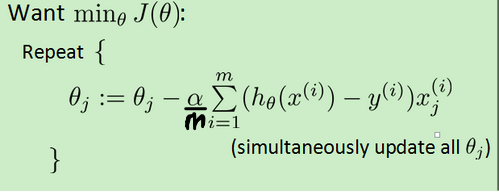
(和线性回归类似,h(x)不同,有除以m)
1.决策边界:对应h(x)=0.5,即theta' * X=0。
2.寻找不同的代价函数使他是凸凹函数。
3.高级优化算法(使用actave代码库):同样适用于线性回归
调用
%‘GradObj’, ‘on’:表示我们实现的函数返回cost和偏导数,否则只返回cost。
%‘MaxIter’, ‘100’:表示至多循环100次
options = optimset(‘GradObj’, ‘on’, ‘MaxIter’, ‘100’);
initialTheta = zeros(2,1);
[optTheta, functionVal, exitFlag]= fminunc(@costFunction, initialTheta, options);%initialTheta必须是>=2
实现函数

4.多分类(分成>2类):一对多
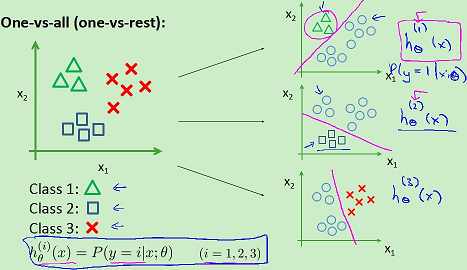
对于一个新的输入,分别带入每个函数,其中值最大的h(x)表示属于这个分类。
- 下半部分:解决过拟合
1.
欠拟合:多项式的项太少,并且高项少,拟合不了。
拟合:训练集中的数据有的没有拟合,但大部分已经拟合,且感觉应该是对的。
过拟合:多项式的项太多,过度拟合,训练集中的数据都完全拟合,拐了好多万,但加入新的数据就会不在拟合。
一般在当有很多特征变量,并且看起来都很有用,而数据集相对少时,容易出现过拟合。
2.过拟合解决办法:
减少特征变量的数量:人工检查重要性,模型选择算法(后面会讲)
正则化:每个特征变量都有用
3.正则化:λ是正则化参数,用来在两个不同的目标中控制一个平衡关系,第一个使更好的拟合训练集(原来的部分),第二是要参数尽量小,从而形式尽量简单,避免过拟合(新加的部分)。λ如果太大,则所有theta[i]=0(i>0),会欠拟合。
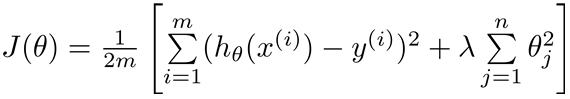
4.正则化的梯度下降算法:
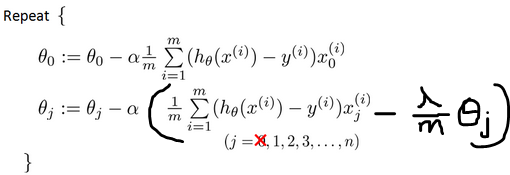
移项: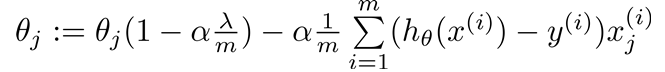
一般让![]() <1(0.99)
<1(0.99)
5.正则化的正规方程解法(下图中的矩阵是(n+1)*(n+1)的,n是特征变量的个数):另偏导数等于0,可解的

注意:可以证明现在括号内的矩阵一定是可逆的!(正则化解决了这个问题)
代码:
1.g(z)函数
function g = sigmoid(z) g = zeros(size(z)); g=1 ./ (1+ e .^ (-z)); end
2.cost函数,用来给系统函数fminunc使用
function [J, grad] = costFunction(theta, X, y) m = length(y); % number of training examples J = 0; grad = zeros(size(theta)); h=sigmoid(X *theta); %改变了!!! J= -( y' * log(h) + (1-y)' * log(1-h) )/m; %代价
grad= (X' *(h-y))/m; %偏导数
end
3.上半部分整体代码
data = load('ex2data1.txt'); X = data(:, [1, 2]); y = data(:, 3); [m, n] = size(X); X = [ones(m, 1) X]; initial_theta = zeros(n + 1, 1); [cost, grad] = costFunction(initial_theta, X, y); options = optimset('GradObj', 'on', 'MaxIter', 400); [theta, cost] = ... fminunc(@(t)(costFunction(t, X, y)), initial_theta, options); plotDecisionBoundary(theta, X, y); p = predict(theta, X); fprintf('Train Accuracy: %f ', mean(double(p == y)) * 100);
4.正则化的cost函数
function [J, grad] = costFunctionReg(theta, X, y, lambda) m = length(y); J = 0; grad = zeros(size(theta)); [J, grad]=costFunction(theta,X,y); %调用非正则化的函数 J=J+(sum(theta .^2 )-theta(1)^2)*lambda/(2.0*m); %theta(1)不正则! grad=grad+theta*lambda/m; grad(1)=grad(1)-theta(1)*lambda/m; end
5.生成多项式函数
function out = mapFeature(X1, X2) %生成每一列代表:X1, X2, X1.^2, X2.^2, X1*X2, X1*X2.^2, etc.. degree = 6; out = ones(size(X1(:,1))); for i = 1:degree for j = 0:i out(:, end+1) = (X1.^(i-j)).*(X2.^j);%表示新增一列,且赋值 end end end
6.画分割线的函数:
函数contour解释:
contour(u,v,z,n)是画等值线
其第四个参数是控制等值线的值的
如果n是一个标量,那么解释为等值线的条数例如
contour(u,v,z,20)那么它会根据数据的范围画出20条等值线
如果n是一个向量,那么解释为需要等值线的值,例如
contour(u,v,z,[1 2 3 4])会画出z=1,2,3,4四个值的等值线
如果我们要只要画指定的某个值的等值线,我们就用两个相同的数组成向量
contour(u,v,z,[1 1]);画值为1的等值线
contour(u,v,z,[0 0]);画值为0的等值线
function plotDecisionBoundary(theta, X, y) plotData(X(:,2:3), y);%输出训练集 hold on if size(X, 2) <= 3 plot_x = [min(X(:,2))-2, max(X(:,2))+2]; plot_y = (-1./theta(3)).*(theta(2).*plot_x + theta(1)); plot(plot_x, plot_y) legend('Admitted', 'Not admitted', 'Decision Boundary') axis([30, 100, 30, 100]) else % Here is the grid range u = linspace(-1, 1.5, 50);%分成50份 v = linspace(-1, 1.5, 50); z = zeros(length(u), length(v)); % Evaluate z = theta*x over the grid for i = 1:length(u) for j = 1:length(v) z(i,j) = mapFeature(u(i), v(j))*theta; end end z = z'; %!!! important to transpose z before calling contour % Plot z = 0 % Notice you need to specify the range [0, 0] contour(u, v, z, [0, 0], 'LineWidth', 2) end hold off end
7.预测代码
function p = predict(theta, X) m = size(X, 1); p = zeros(m, 1); p=sigmoid(X * theta); p=(p>=0.5); end
8.下半部分整体代码
data = load('ex2data2.txt'); X = data(:, [1, 2]); y = data(:, 3); %plotData(X, y); X = mapFeature(X(:,1), X(:,2)); %生成多项式 initial_theta = zeros(size(X, 2), 1); lambda = 1; %数值选取需要注意,可以画出图来试试 [cost, grad] = costFunctionReg(initial_theta, X, y, lambda); fprintf('Cost at initial theta (zeros): %f ', cost); initial_theta = zeros(size(X, 2), 1); lambda = 1; options = optimset('GradObj', 'on', 'MaxIter', 400); [theta, J, exit_flag] = ... fminunc(@(t)(costFunctionReg(t, X, y, lambda)), initial_theta, options); plotDecisionBoundary(theta, X, y); p = predict(theta, X); %预测准确度 fprintf('Train Accuracy: %f ', mean(double(p == y)) * 100);