本文将主要讲述在堆排序和优先级队列中使用的一种数据结构,二叉堆;
一、结构概述
完全二叉堆,首先在逻辑上是树形结构,完全二字则表明是完全的二叉树,其结构如图所示:
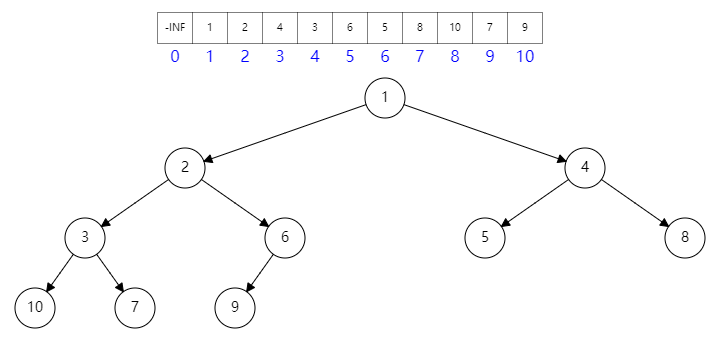
结构性: 正是因为是完全结构的二叉树,所以可以将节点映射到数组中,其运算关系如下,i 表示数组下标:
- 父节点:
(i - 1) >> 1; - 左孩子:
1 + (i << 1); - 右孩子:
(1 + i) << 1;
堆序性: 在堆结构中,其任一父节点的优先级都高于其子节点,图中的数字越小,表示优先级越高;
API: 对于堆结构而言,最重要的几个接口:
insert() // 插入节点
getMax() // 获取优先级最高的节点
delMax() // 删除优先级最高的节点
二、插入节点
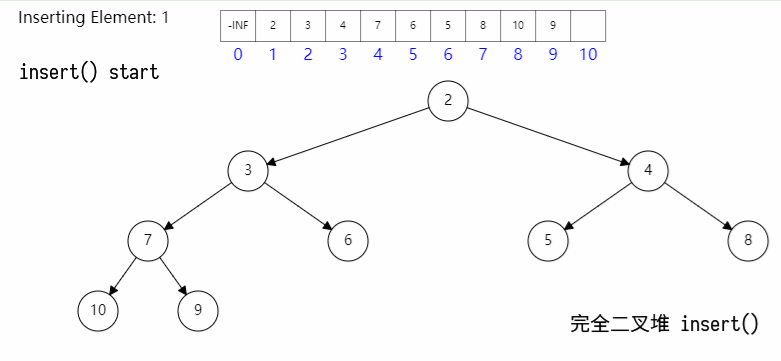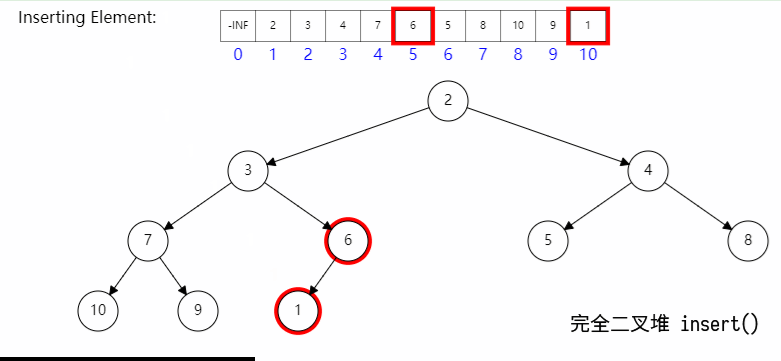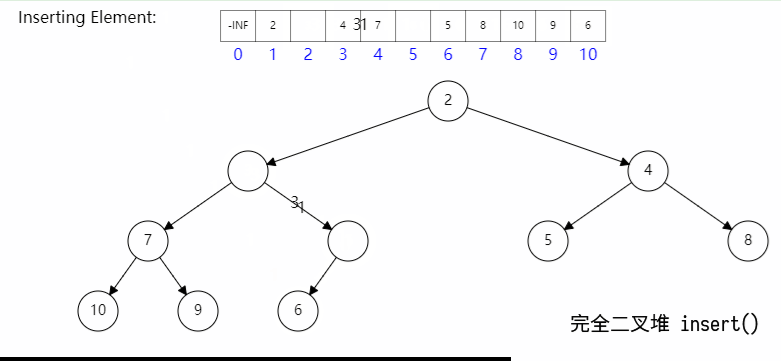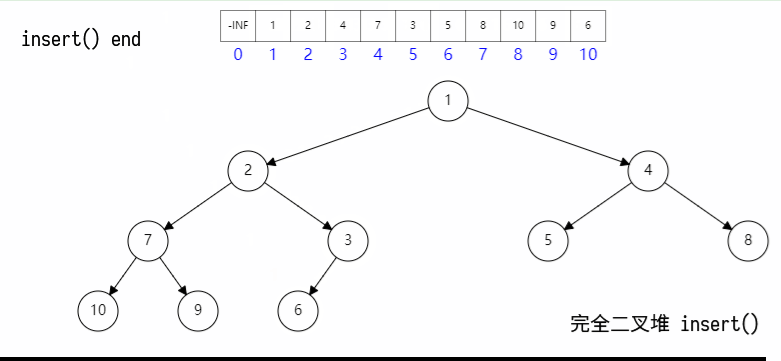
插入节点时候主要分两步:
- 首先将节点插入队尾,对于数组而言其时间复杂度为
O(1); - 然后与其父节点比较,如果新节点优先级更高,则与父节点交换,直至其优先级不大于父节点;(此过程称为上滤)
其具体过程如图所示:
其代码如下:
public void insert(E e) {
if (size == data.length) throw new IllegalArgumentException("heap is full");
data[size] = e;
siftUp(size);
size++;
}
private int siftUp(int i) {
while (i > 0) { // 还有父节点
int p = parent(i);
if (cmp(data[i], data[p]) <= 0) break;
swap(i, p);
i = p;
}
return i;
}
private void swap(int i, int j) {
Object t = data[i];
data[i] = data[j];
data[j] = t;
}
三、删除、获取节点
删除首节点时候同样分两步:
- 首先用队尾的节点替换首节点;
- 然后与两个子节点比较,如果父节点优先级不是最高,则用子节点中优先级最高的节点替换,直至父节点的优先级最高;(此过程称为下滤)
其具体过程如图所示:
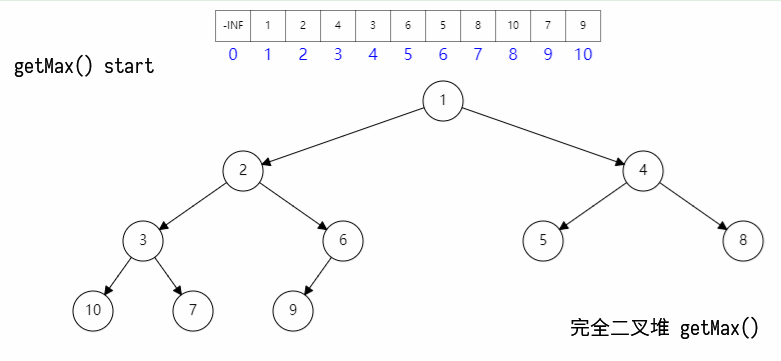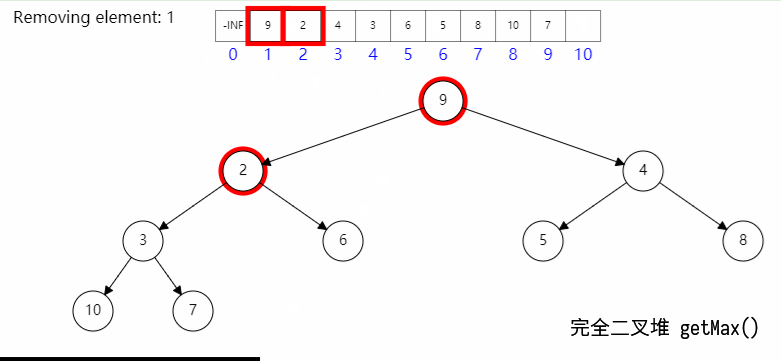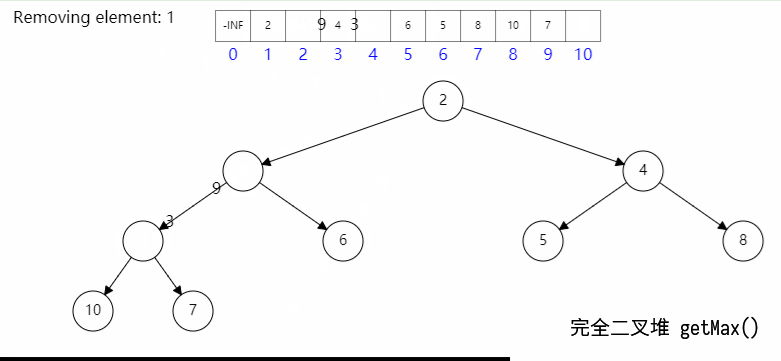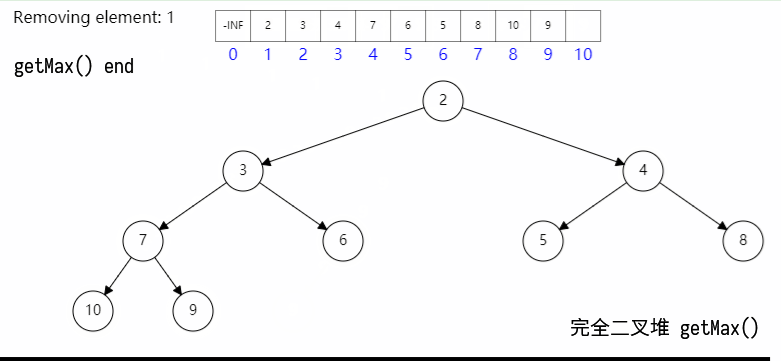
具体代码如下:
public E delMax() {
E e = (E) data[0];
data[0] = data[--size];
shiftDown(0);
return e;
}
private int shiftDown(int i) {
int j;
while (i != (j = properParent(i))) { // 如果父节点优先级不是最高
swap(i, j);
i = j;
}
return i;
}
private int properParent(int i) {
int l = lc(i);
if (l >= size) return i;
int max = cmp(data[i], data[l]) >= 0 ? i : l;
int r = rc(i);
if (r >= size) return max;
return cmp(data[max], data[r]) >= 0 ? max : r;
}
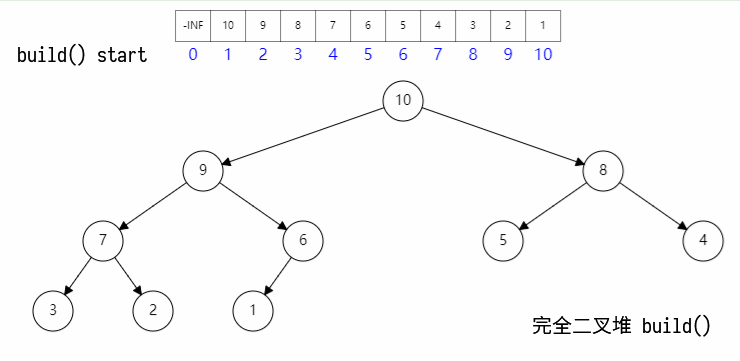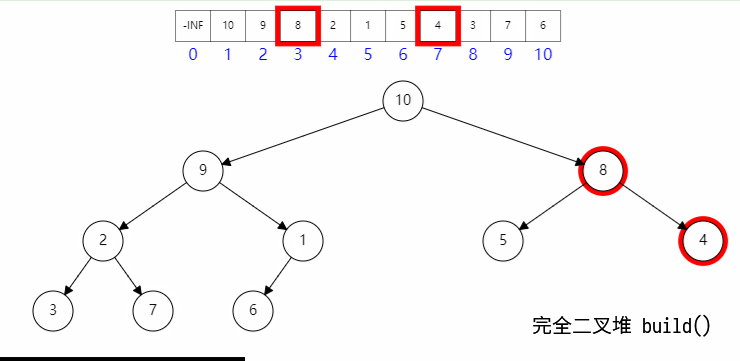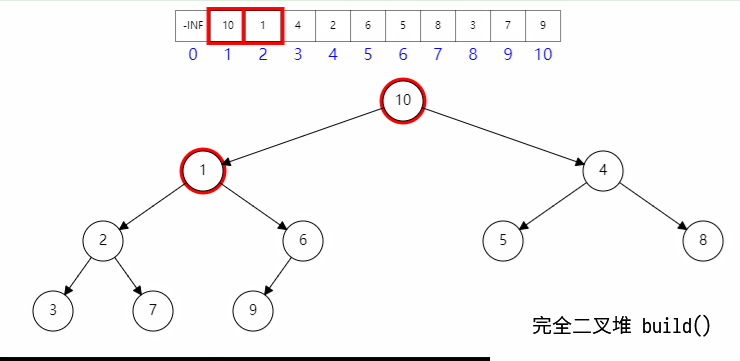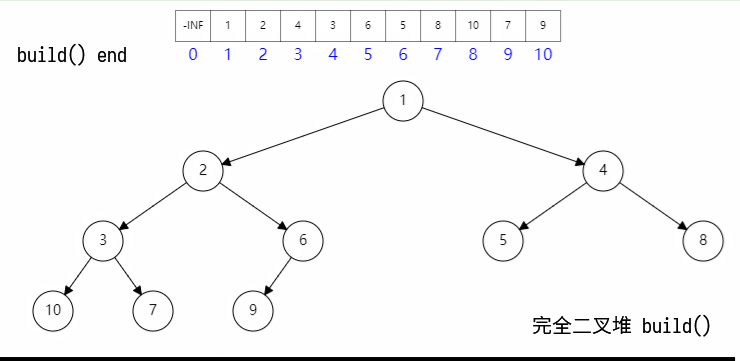
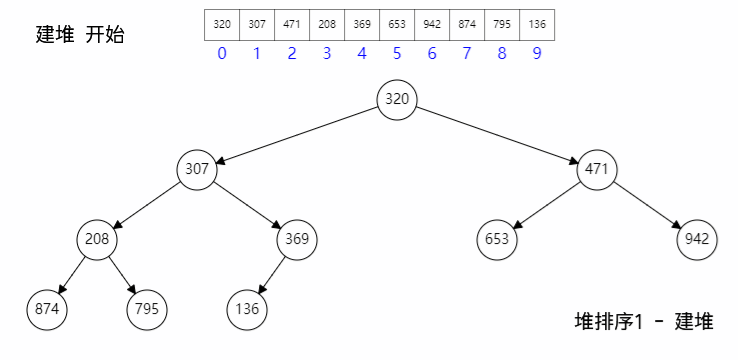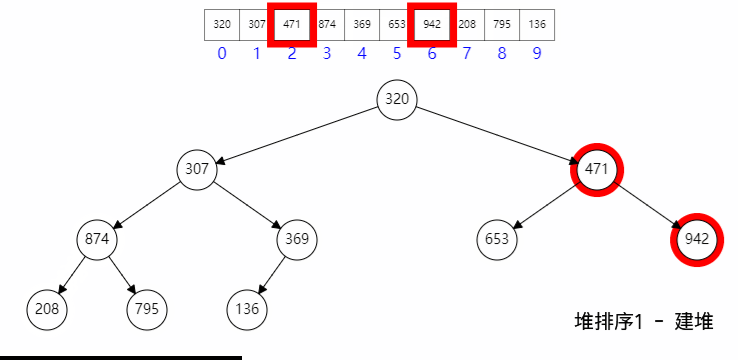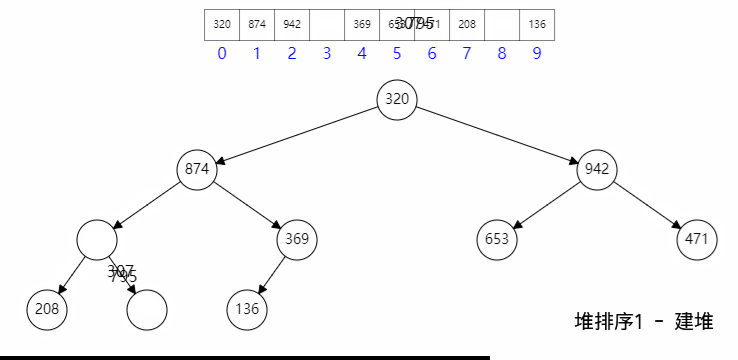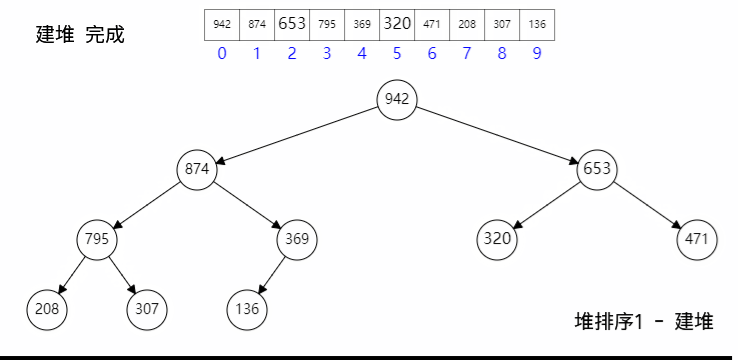
四、建堆
建堆的时候:
- 首先构建二叉堆数组;
- 然后最后一个父节点开始向上,一次执行下滤;
其具体过程如图所示:
具体代码如下:
public void build() {
for (int i = parent(size - 1); i > -1 && i < size; i--)
shiftDown(i);
}
五、堆排序
堆排序的整个过程,可以将数组分成两个部分,完全二叉堆部分和已排序部分,每次将堆的首节点和尾节点交换,同时已排序部分加一,然后二叉堆复位,一直重复指到堆为空;
其具体过程如下:
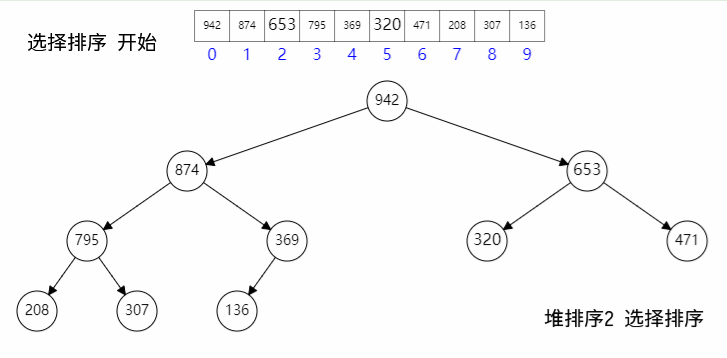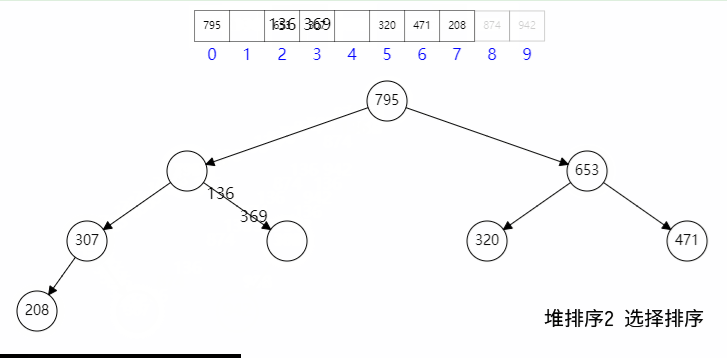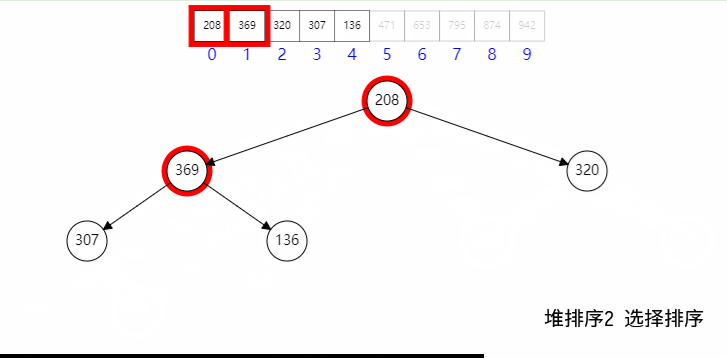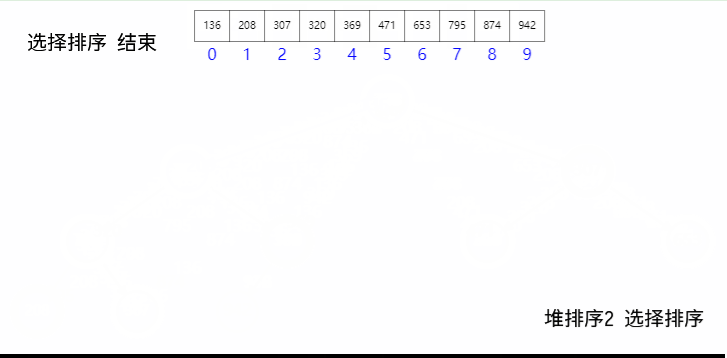
其具体代码如下:
public void heapSort(int hi) {
// 建堆
while (size > 0) data[--hi] = delMax();
}
总结
- 对于完全二叉堆而言,它本质的特征是堆序性,只是当其构成完全二叉树的时候,可以直接使用数组表示,其查询的效率更高;