bzoj1177&p3625 [APIO2009]采油区域p[大力讨论]

我好菜菜啊。

给定矩形，从中选出三个边长K的正方形互不重叠，使得覆盖到的数总和最大。

---

想的时候往dp上钻去了。。结果一开始想了一个错的dp，像这样

/**************************************************************
    Problem: 1177
    User: stealthassassin
    Language: C++
    Result: Wrong_Answer
****************************************************************/
 
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define dbg(x) cerr<<#x<<" = "<<x<<endl
#define ddbg(x,y) cerr<<#x<<" = "<<x<<"   "<<#y<<" = "<<y<<endl
using namespace std;
typedef long long ll;
template<typename T>inline char MIN(T&A,T B){return A>B?A=B,1:0;}
template<typename T>inline char MAX(T&A,T B){return A<B?A=B,1:0;}
template<typename T>inline T _min(T A,T B){return A<B?A:B;}
template<typename T>inline T _max(T A,T B){return A>B?A:B;}
template<typename T>inline T _max(T A,T B,T C){return _max(A,_max(B,C));}
template<typename T>inline T read(T&x){
    x=0;int f=0;char c;while(!isdigit(c=getchar()))if(c=='-')f=1;
    while(isdigit(c))x=x*10+(c&15),c=getchar();return f?x=-x:x;
}
const int N=1500+7;
ll sum[N][N];
int f[N][N][3],n,m,A;
inline int get_sum(int xa,int ya,int xb,int yb){return sum[xb][yb]-sum[xa][yb]-sum[xb][ya]+sum[xa][ya];}
 
int main(){//freopen("test.in","r",stdin);freopen("test.out","w",stdout);
    read(n),read(m),read(A);
    for(register int i=1;i<=n;++i)for(register int j=1;j<=m;++j)sum[i][j]=read(sum[i][j])+sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
    for(register int k=1;k<=3;++k)for(register int i=A;i<=n;++i)for(register int j=A;j<=m;++j)
    f[i][j][k]=_max(f[i-1][j][k],f[i][j-1][k],_max(f[i-A][j][k-1],f[i][j-A][k-1])+get_sum(i-A,j-A,i,j));//ddbg(i,j),ddbg(k,f[i][j][k]);
    printf("%d
",f[n][m][3]);
    return 0;
}

结果WA。还发现竟然骗了40pts。很快就发现dp推得有问题。明显没有办法用简单的dp状态来表示，想了一会复杂的dp方法，想不出来，然后就觉得这题DP不可做。然后陷入了僵局，尝试各种乱七八糟的做法却无果。

之后翻题解才发现，你3个正方形，个数那么少，用不了dp，那明摆着就是让你研究他们相对位置关系嘛。。

所以下面大力讨论一下，最大答案就有了这几种可能分布情况（红线表示区块的分界）：

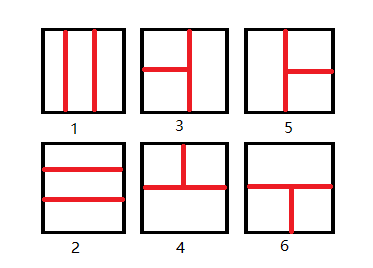
所以只要对每种情况都找一下最大总和，具体就是枚举边界线，3456四种分别二重横竖枚举$O(nm)$，每个区块里找最大值矩形，这个可以用前缀和加递推提前预处理，看code。

12就枚举一条边界线，然后中间那块不妨是k宽度的也没问题，在k宽度中找一个最大的，再配上边上两块最大的。

所以这题代码真的是写的恶心。。。而且BZOJ数据有锅，用快读还超时。。做了近4小时，心态有点崩溃。。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define dbg(x) cerr<<#x<<" = "<<x<<endl
#define ddbg(x,y) cerr<<#x<<" = "<<x<<"   "<<#y<<" = "<<y<<endl
#define rep(i,x,y) for(register int i=x;i<=y;++i)
#define per(i,x,y) for(register int i=x;i>=y;--i)
using namespace std;
typedef long long ll;
template<typename T>inline char MIN(T&A,T B){return A>B?A=B,1:0;}
template<typename T>inline char MAX(T&A,T B){return A<B?A=B,1:0;}
template<typename T>inline T _min(T A,T B){return A<B?A:B;}
template<typename T>inline T _max(T A,T B){return A>B?A:B;}
template<typename T>inline T _max(T A,T B,T C){return _max(A,_max(B,C));}
//namespace io
//{
//    const int SIZE = (1 << 21) + 1;
//    char ibuf[SIZE], *iS, *iT, obuf[SIZE], *oS = obuf, *oT = oS + SIZE - 1, c, qu[55]; int f, qr;
//    #define gc() (iS == iT ? (iT = (iS = ibuf) + fread (ibuf, 1, SIZE, stdin), (iS == iT ? EOF : *iS ++)) : *iS ++)
//    inline void flush (){fwrite (obuf, 1, oS - obuf, stdout);oS = obuf;}
//    inline void putc (char x){*oS ++ = x;if (oS == oT) flush ();}
//    template <class I>
//    inline void read(I &x) {for (f = 1, c = gc(); c < '0' || c > '9'; c = gc()) if (c == '-') f = -1;
//        for (x = 0; c <= '9' && c >= '0'; c = gc()) x = x * 10 + (c & 15); x *= f;}
//    template <class I>
//    inline void print (I x){
//        if (!x) putc ('0'); if (x < 0) putc ('-'), x = -x;while(x) qu[++ qr] = x % 10 + '0',  x /= 10;while (qr) putc (qu[qr--]);}
//    struct Flusher_ {~Flusher_(){flush();}}io_flusher_;
//}
//using io::read;
//using io::putc;
//using io::print;
const int N=1500+5;
int a[N][N],zs[N][N],ys[N][N],zx[N][N],yx[N][N],ans;
int n,m,k;

int main(){//freopen("tmp.in","r",stdin);freopen("tmp.out","w",stdout);
    cin>>n>>m>>k;
    rep(i,1,n)rep(j,1,m)scanf("%d",&a[i][j]),a[i][j]+=a[i][j-1];
    rep(i,1,n)rep(j,1,m)a[i][j]+=a[i-1][j];
    per(i,n,k)per(j,m,k)a[i][j]=a[i][j]-a[i-k][j]-a[i][j-k]+a[i-k][j-k];
    rep(i,k,n)rep(j,k,m)zs[i][j]=max(a[i][j],max(zs[i-1][j],zs[i][j-1]));
    rep(i,k,n)per(j,m,k)ys[i][j]=max(a[i][j],max(ys[i-1][j],ys[i][j+1]));
    per(i,n,k)rep(j,k,m)zx[i][j]=max(a[i][j],max(zx[i+1][j],zx[i][j-1]));
    per(i,n,k)per(j,m,k)yx[i][j]=max(a[i][j],max(yx[i+1][j],yx[i][j+1]));
    rep(i,k,n-2*k)rep(j,k,m)ans=max(ans,zs[i][m]+a[i+k][j]+yx[i+k*2][k]);
    rep(i,k,m-2*k)rep(j,k,n)ans=max(ans,zs[n][i]+a[j][i+k]+yx[k][i+k*2]);
    rep(i,k,n-k)rep(j,k,m-k)ans=max(ans,zs[i][j]+ys[i][j+k]+yx[i+k][k]);
    rep(i,k,n-k)rep(j,k,m-k)ans=max(ans,zx[i+k][j]+yx[i+k][j+k]+zs[i][m]);
    rep(i,k,m-k)rep(j,k,n-k)ans=max(ans,zs[j][i]+zx[j+k][i]+yx[k][i+k]);
    rep(i,k,m-k)rep(j,k,n-k)ans=max(ans,ys[j][i+k]+yx[j+k][i+k]+zs[n][i]);
    printf("%d
",ans);
    return 0;
}