一、欧几里得相似度理论
参考:https://blog.csdn.net/qq_37142346/article/details/80455266
二、代码实现
1)创建df,使用 spark.createDataFrame(rdd,schema)
val spark = SparkSession.builder().appName("euclidean").master("local[*]").getOrCreate() val schema = StructType(Seq( StructField("userid",StringType,false), StructField("apple",DoubleType,false), StructField("banana",DoubleType,false), StructField("orange",DoubleType,false), StructField("watermelon",DoubleType,false), StructField("melon",DoubleType,false) )) val df = spark.createDataFrame(spark.sparkContext.parallelize(Seq( Row("nol",4.5,5.0,0.0,3.0,0.0), Row("no2",0.0,0.0,5.0,4.0,0.0), Row("no3",4.0,3.0,4.5,0.0,4.0), Row("no4",0.0,0.0,0.0,0.0,5.0), Row("no5",4.0,3.0,2.0,1.0,0.0) )),schema)
2)过滤不需要的列
val cls = df.columns.filter(x => x != "userid").map(x=>col(x))
3)合并列:DF => Iterator[Row] => List[Row] => List[Array[Double]]
// List[Row] val rdd = df.select(concat_ws(",", cls: _*).alias("feature")).rdd.toLocalIterator.toList // List[Array[Double]] .map(r => {
// Row是一个集合,需要取值r(0)才能拿到里面的数据 val arr = r(0).toString.split(",").map(x => x.toDouble) arr }) eucli(rdd).foreach(println(_))
spark.stop()
4)计算pairwise相似度方法(for循环套for循环)
def eucli(rdd:List[Array[Double]])={ val lst:ListBuffer[ListBuffer[Double]] = ListBuffer[ListBuffer[Double]]() for (arr<-rdd){ val sec:ListBuffer[Double]=ListBuffer[Double]() for(a1<-rdd){ // 欧式距离 // sec.append(calcEuc(arr,a1)) // 余弦相似度 sec.append(calCos(arr,a1)) } lst.append(sec) } lst }
5)欧式距离公式
//欧氏距离公式 def calcEuc(arr1:Array[Double],arr2:Array[Double])={ val lst:ListBuffer[Double] = ListBuffer[Double]()
// if num1 == num2 这点判断很重要,否则不能保证只处理相同下标 for (num1<-0 until arr1.length;num2<-0 until arr2.length;if num1==num2){ lst.append(math.pow(arr1(num1)-arr2(num2),2)) } 1/(1+math.sqrt(lst.sum)) }
二、余弦相似度
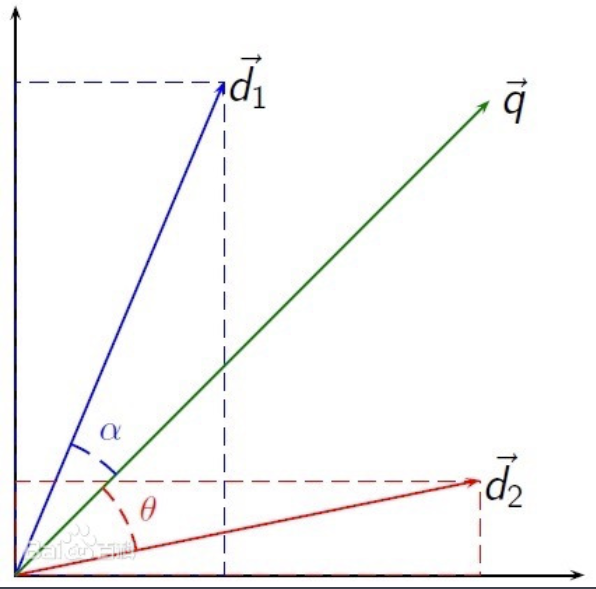
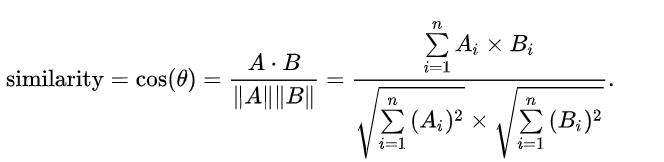
//余弦相似度 def calCos(arr1:Array[Double],arr2:Array[Double]):Double={ dot_product(arr1,arr2)/(mod(arr1)*mod(arr2)) } // 点积 def dot_product(arr1:Array[Double],arr2:Array[Double]):Double={ arr1.zip(arr2).map({case (x,y)=>x*y}).sum } // 向量求模 def mod(arr:Array[Double]): Double ={ math.sqrt(arr.map(math.pow(_,2)).sum) }
三、欧式相似度和余弦相似度的区别
https://www.zhihu.com/question/19640394
引用一段比较认可的说法
>>>
余弦夹角可以有效规避个体相同认知中不同程度的差异表现,更注重维度之间的差异,而不注重数值上的差异;
反过来思考,当向量夹角的余弦值较小(差异很大)时,欧氏距离可以很小(差异很小),如(0,1)和(1,0)两个点
所以如果要对电子商务用户做聚类,区分高价值用户和低价值用户,用消费次数和平均消费额,这个时候用余弦夹角是不恰当的,
因为它会将(2,10)和(10,50)的用户算成相似用户,但显然后者的价值高得多,因为这个时候需要注重数值上的差异,而不是维度之间的差异。
Overall,余弦相似度衡量的是维度间相对层面的差异,欧氏度量衡量数值上差异的绝对值
作者:joegh
链接:https://www.zhihu.com/question/19640394/answer/12484677
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
>>>