输入:一些点的坐标;一个测试点
输出:是否在多边形内部
思路:
(1)面积和判别法:判断目标点与多边形的每条边组成的三角形面积和是否等于该多边形,相等则在多边形内部。
(2)夹角和判别法:判断目标点与所有边的夹角和是否为360度,为360度则在多边形内部。
(3)引射线法:从目标点出发引一条射线,看这条射线和多边形所有边的交点数目。如果有奇数个交点,则说明在内部,如果有偶数个交点,则说明在外部。
具体做法:将测试点的Y坐标与多边形的每一个点进行比较,会得到一个测试点所在的行与多边形边的交点的列表。在下图的这个例子中有8条边与测试点所在的行相交,而有6条边没有相交。如果测试点的两边点的个数都是奇数个则该测试点在多边形内,否则在多边形外。在这个例子中测试点的左边有5个交点,右边有三个交点,它们都是奇数,所以点在多边形内。
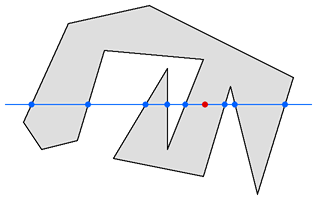
算法图解:

想法:
1、先求出这些点中的横纵坐标的最大值和最小值,判断测试点是否在内部,若不在,则直接排除掉,返回false;
if(p.x<minx || p.x>maxx || p.y<miny ||p.y>maxy)
{
return false;
}
2、核心部分:
循环每一个边;
被测试点纵坐标testy是否在相邻两点纵坐标之内?
待测点testx是否在两点连线下方,若是,则记录一次,说明延长线上有一个交点。
最后判断记录次数为奇数,则在多边形内部。

1 int pnpoly(int nvert, float *vertx, float *verty, float testx, float testy) 2 { 3 int i, j, c = 0; 4 for (i = 0, j = nvert-1; i < nvert; j = i++) 5 { 6 if ( ((verty[i]>testy) != (verty[j]>testy)) && 7 (testx < (vertx[j]-vertx[i]) * (testy-verty[i]) / (verty[j]-verty[i]) + vertx[i]) ) 8 c = !c; 9 } 10 return c; 11 }
