示例无向图如下:(起始点为v0)

邻接矩阵为:
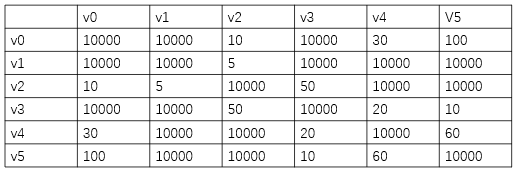
注意:其中没有连接的边和自己到自己的点权值用10000表示。
代码:
static void Main(string[] args) {
int[,] graph = new int[,] { { 10000, 10000, 10, 10000, 30, 100 }, { 10000, 10000, 5, 10000, 10000, 10000 }, { 10, 5, 10000, 50, 10000, 10000 }, { 10000, 10000, 50, 10000, 10000, 10 }, { 30, 10000, 10000, 20, 10000, 60 }, { 100, 10000, 10000, 10, 60, 10000 } };
int n = 6;
int[] S = new int[n]; //最短路径的顶点集合 string[] mid = new string[n];//点的路线 for (int i = 0; i < n; i++) { S[i] = 0; mid[i] = ""; } ShortestPathByDijkstra(n, graph, S, mid);
} public static int IsContain(int m,int[] S)//判断该顶点是否已经计算过 { int index = -1; for (int i = 1; i < 6; i++) { if (S[i] == m) { index = i; } } return index; }
/// <summary> /// Dijkstrah实现最短路算法 /// </summary> static void ShortestPathByDijkstra(int n,int[,] graph, int[] S, string[] mid) { int min; int next; for (int f = n-1; f > 0; f--) { //置为初始值 min = 1000; next = 0;//第一行最小的元素所在的列 next点 //找出第一行最小的列值 for (int j = 1; j < n; j++)//循环第0行的列 { if ((IsContain(j,S) == -1) && (graph[0, j] < min))//不在S中,找出第一行最小的元素所在的列 { min = graph[0, j]; next = j; } } //将下一个点加入S S[next] = next; if (min == 1000) { Console.WriteLine("V0到V{0}的最短路径为:无", next); } else { Console.WriteLine("V0到V{0}的最短路径为:{1},路径为:V0{2}->V{0}", next, min, mid[next]); } // 重新初始0行所有列值 for (int j = 1; j < n; j++)//循环第0行的列 { if (IsContain(j,S) == -1)//初始化除包含在S中的 { if ((graph[next, j] + min) < graph[0, j])//如果小于原来的值就替换 { graph[0, j] = graph[next, j] + min; mid[j] = mid[next] + "->V" + next;//记录过程点 } } } } }
结果

解析:
分三部分,主函数中给出图中的初始邻接矩阵,顶点个数。以及初始化最短路径的顶点集合和点路线集合。
IsContain(int m,int[] S)这个函数是在每次循环的时候判断该点是否已经在最短路径集合中,即已经遍历过。
接下来就是Dijkstra算法,大致步骤如下:
1、添加初始顶点v0在集合S中,遍历第一行,找最小的权值所在的顶点列值j。
2、将j值做为下一个点加入集合S中,输出此时到达j点的最小路径。
3、重新初始化第一行的值,通过判断加入某点后graph[next][j]+min是否小于graph[0, j](其中j不在集合S中),若是则替换后者,并记录此过程 mid[j] = mid[next] + "->V" + next;
4、循环1、2、3步骤顶点数-1次。
详细参考:https://blog.csdn.net/qq_25954259/article/details/78289335?locationNum=5&fps=1