简单插入排序
从数组的第二个元素开始,依次向前进行对比,如果前面的元素大,则后移。重复数组长度-1 轮。工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
算法描述
- 从第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,在已经排序的元素序列中从后向前扫描
- 如果该元素(已排序)大于新元素,将该元素移到下一位置
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
- 将新元素插入到该位置后
- 重复步骤2~5
动图演示
实例验证
10000个数字组成的数组排序,耗时大概率在200ms-300ms。

public class TestInsertionSort { public static void main(String[] args) { System.out.println("old:" + Arrays.asList(InsertionData.array).toString() + "..."); Long start = System.currentTimeMillis(); sort(InsertionData.array); Long end = System.currentTimeMillis(); System.out.println("new:" + Arrays.asList(InsertionData.array).toString() + "..."); System.out.println("耗时:" + (end - start)); } /** * 1.从第一个元素开始,该元素可以认为已经被排序 <br> * 2.取出下一个元素,在已经排序的元素序列中从后向前扫描 <br> * 3.如果该元素(已排序)大于新元素,将该元素移到下一位置 <br> * 4.重复步骤3,直到找到已排序的元素小于或者等于新元素的位置 <br> * 5.将新元素插入到该位置后 <br> * 6.重复步骤2~5 */ static void sort(Integer[] array) { // 外层循环控制比较轮次 for (Integer i = 1; i < array.length; i++) { Integer standard = array[i]; Integer j; // 内层循环控制比较逻辑 for (j = i; j > 0; j--) { if (array[j - 1] <= standard) { // 数据已符合排序规则 break; } if (array[j - 1] > standard) { // 比基准元素大的,依次后移 array[j] = array[j - 1]; } } // 将基准元素插入到相应位置 if (j != i) { array[j] = standard; } System.out.println("sorting:" + Arrays.asList(array).toString() + "..."); } } } class InsertionData { public static Integer[] array; static { array = new Integer[10]; for (Integer i = 0; i < 10; i++) { Random r = new Random(); array[i] = r.nextInt(100); } } }
结果展示:
old:[15, 96, 78, 2, 10, 70, 96, 7, 95, 90]... sorting:[15, 96, 78, 2, 10, 70, 96, 7, 95, 90]... sorting:[15, 78, 96, 2, 10, 70, 96, 7, 95, 90]... sorting:[2, 15, 78, 96, 10, 70, 96, 7, 95, 90]... sorting:[2, 10, 15, 78, 96, 70, 96, 7, 95, 90]... sorting:[2, 10, 15, 70, 78, 96, 96, 7, 95, 90]... sorting:[2, 10, 15, 70, 78, 96, 96, 7, 95, 90]... sorting:[2, 7, 10, 15, 70, 78, 96, 96, 95, 90]... sorting:[2, 7, 10, 15, 70, 78, 95, 96, 96, 90]... sorting:[2, 7, 10, 15, 70, 78, 90, 95, 96, 96]... new:[2, 7, 10, 15, 70, 78, 90, 95, 96, 96]... 耗时:1
复杂度分析
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(n²) | O(n²) | O(n²) | O(1) |
插入排序所需的时间取决于输入元素的初始顺序。例如,对一个很大且其中的元素已经有序(或接近有序)的数组进行排序将会比随机顺序的数组或是逆序数组进行排序要快得多。
希尔排序
希尔排序又叫缩小增量排序。希尔排序步长从大到小调整,第一次循环后面元素逐个和前面元素按间隔步长进行比较并交换,直至步长为1,步长选择是关键。
算法描述
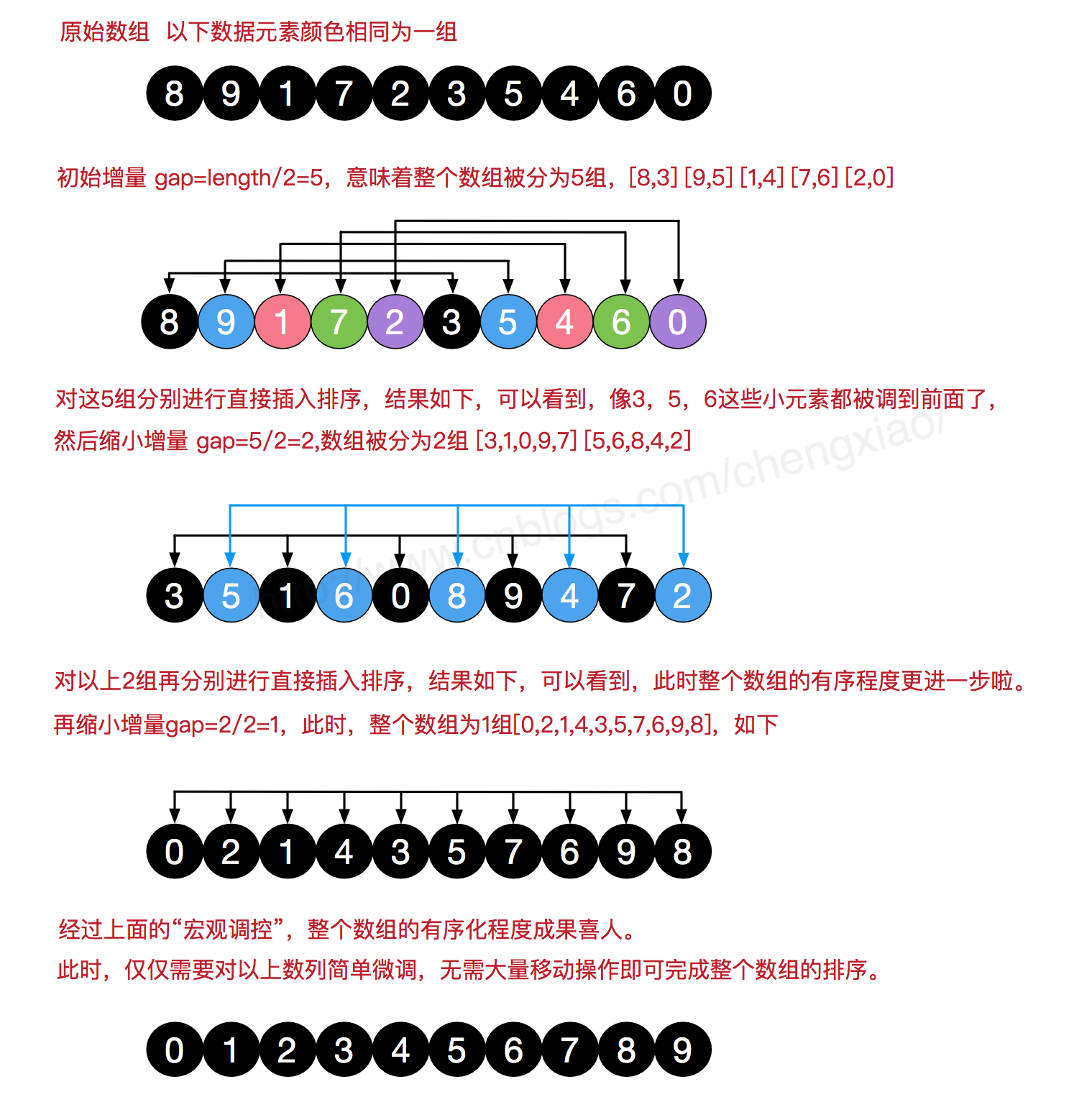
动图演示
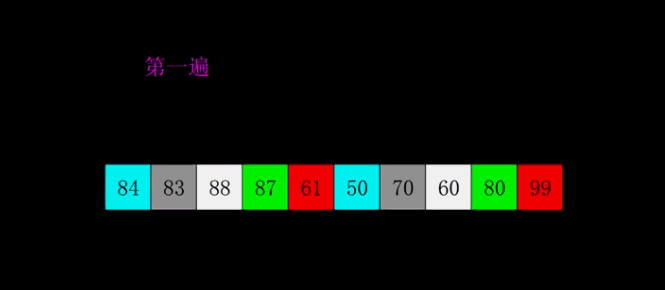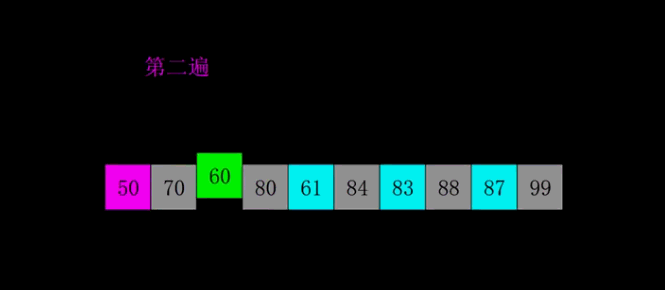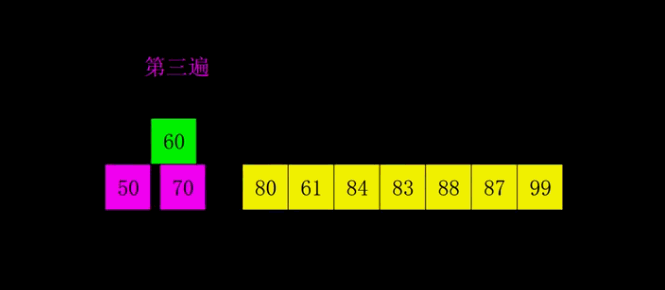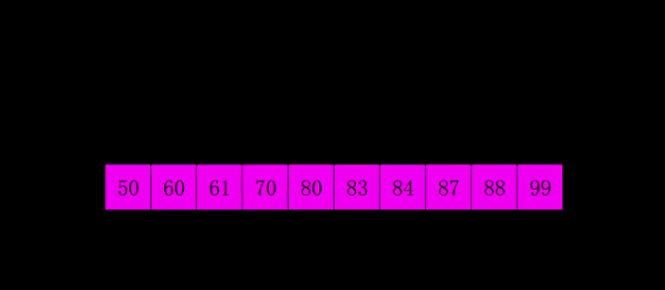
实例验证
10000个数字组成的数组排序,耗时大概率在20ms左右。

public class TestShellSort { public static void main(String[] args) { System.out.println("old:" + Arrays.asList(ShellData.array).toString() + "..."); Long start = System.currentTimeMillis(); sort(ShellData.array); Long end = System.currentTimeMillis(); System.out.println("new:" + Arrays.asList(ShellData.array).toString() + "..."); System.out.println("耗时:" + (end - start)); } /** */ static void sort(Integer[] array) { int len = array.length; // 步长调整,按照数组长度依次减半,直到最后一次步长为1 for (int step = len / 2; step > 0; step = step / 2) { for (int i = 0; i < step; i++) { // 分组处理,对每个分组进行插入排序 for (int j = i + step; j < len; j += step) {// 外层循环控制比较轮次 Integer standard = array[j]; Integer k; for (k = j; k > 0 && (k - step) >= 0; k -= step) {// 内层循环控制比较逻辑 if (array[k - step] <= standard) { // 数据已符合排序规则 break; } if (array[k - step] > standard) { // 比基准元素大的,依次后移 array[k] = array[k - step]; } } // 将基准元素插入到相应位置 if (k != j) { array[k] = standard; } } } System.out.println("sorting:" + Arrays.asList(array).toString() + "..."); } } } class ShellData { public static Integer[] array; static { array = new Integer[10]; for (Integer i = 0; i < 10; i++) { Random r = new Random(); array[i] = r.nextInt(100); } } }
结果展示:
old:[32, 54, 67, 18, 67, 46, 96, 96, 0, 59]... sorting:[32, 54, 67, 0, 59, 46, 96, 96, 18, 67]... sorting:[18, 0, 32, 46, 59, 54, 67, 67, 96, 96]... sorting:[0, 18, 32, 46, 54, 59, 67, 67, 96, 96]... new:[0, 18, 32, 46, 54, 59, 67, 67, 96, 96]... 耗时:0
复杂度分析
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(nlog2 n) | O(nlog2 n) | O(nlog2 n) | O(1) |
希尔排序更高效的原因是它权衡了子数组的规模和有序性。排序之初,各个子数组都很短,排序之后子数组都是部分有序的,这两种情况都很适合插入排序。
