CodeForces

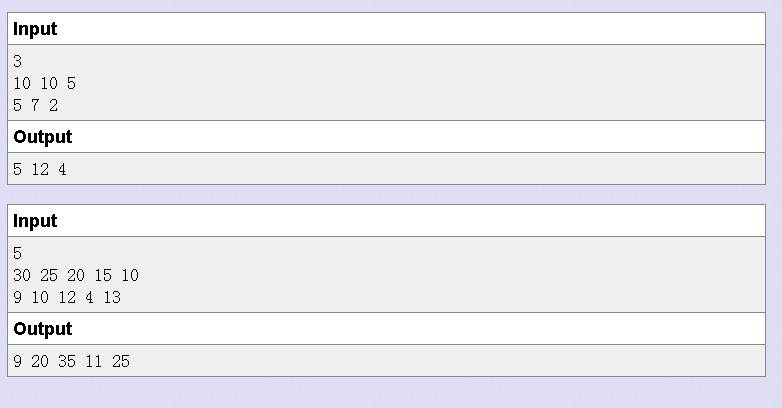
题意：

n天。

每天你会堆一堆雪，体积为 v[i]。每天都有一个温度 t[i] 所有之前堆过的雪在第 i 天体积都会减少 t[i] 。

输出每天融化了的雪的体积。

这个题的正解我怎么想都很难理解，但是慢慢理解了。

计算一个 t[i] 的前缀和 sum。

那么到第 j 天时，设第 i 堆雪融化的体积是 V，则 V = min (sum [ j ] - sum[ i-1], v[ i ] )

所以把 v[ i ] + sum[ i -1] 加入优先队列里，就可以只处理所有当天能化完的雪了。

若 sum[ j ] - v [i] + sum[i - i] <= 0，则证明第 i 堆雪在第 j 天能化完，对答案贡献为V。

否则对答案贡献为 t[i] 。

#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;

#define maxn 100000 + 1000
typedef long long LL;

int main()
{
    int n;
    scanf("%d", &n);

    int v[maxn], t[maxn];
    for (int i = 1; i <= n; i++)
        scanf("%d", &v[i]);

    LL sum[maxn];
    sum[0] = 0;

    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &t[i]);
        sum[i] = sum[i-1] + t[i];
    }

    priority_queue<LL, vector<LL>, greater<LL> > q;
    for (int i = 1; i <= n; i++)
    {
        q.push(v[i] + sum[i-1]);
        LL ans = 0;
        while(!q.empty())
        {
            LL x = q.top();
            if (sum[i]-x >= 0)//这堆雪第 i 天能够融化
            {
                ans += t[i] - (sum[i]-x); 
                q.pop();
            }
            else break; // 否则后面的都化不完了
        }
        ans += q.size() * t[i];

        printf("%lld%c", ans, i==n? '
':' ');
    }
}