1.1.1 摘要
Trie树,又称字典树,单词查找树或者前缀树,是一种用于快速检索的多叉树结构,如英文字母的字典树是一个26叉树,数字的字典树是一个10叉树。
三叉搜索树是一种特殊的Trie树的数据结构,它是数字搜索树和二叉搜索树的混合体。它既有数字搜索树效率优点,又有二叉搜索树空间优点。
在接下来的博文中,我们将介绍Trie树和三叉搜索树的定义,实现和优缺点。
本文目录
1.1.2 正文
Trie树的定义
Trie树与二叉搜索树不同,键不是直接保存在节点中,而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀(prefix),也就是这个节点对应的字符串,而根节点对应空字符串。一般情况下,不是所有的节点都有对应的值,只有叶子节点和部分内部节点所对应的键才有相关的值。
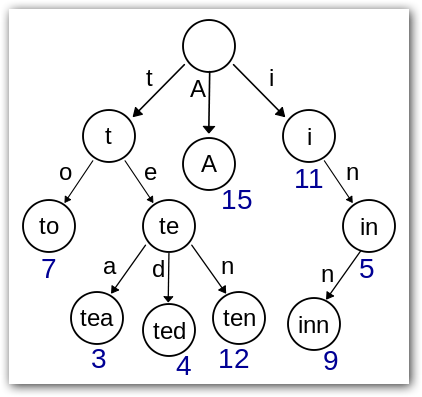
Trie树可以利用字符串的公共前缀来节约存储空间,如下图所示,该Trie树用11个节点保存了8个字符串tea,ted,ten,to,A,i,in,inn。
图1Trie树(图片源于wiki)
我们注意到Trie树中,字符串tea,ted和ten的相同的前缀(prefix)为“te”,如果我们要存储的字符串大部分都具有相同的前缀(prefix),那么该Trie树结构可以节省大量内存空间,因为Trie树中每个单词都是通过character by character方法进行存储,所以具有相同前缀单词是共享前缀节点的。
当然,如果Trie树中存在大量字符串,并且这些字符串基本上没有公共前缀,那么相应的Trie树将非常消耗内存空间,Trie的缺点是空指针耗费内存空间。
Trie树的基本性质可以归纳为:
(1)根节点不包含字符,除根节点外的每个节点只包含一个字符。
(2)从根节点到某一个节点,路径上经过的字符连接起来,为该节点对应的字符串。
(3)每个节点的所有子节点包含的字符串不相同。
Trie树的实现
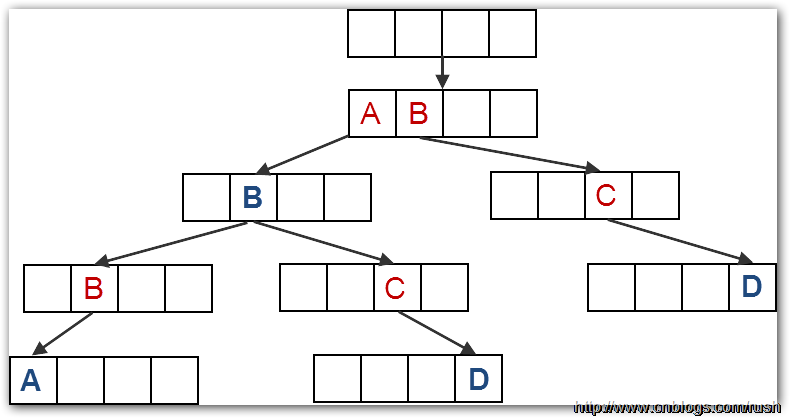
Trie树是一种形似树的数据结构,它的每个节点都包含一个指针数组,假设,我们要构建一个26个字母的Trie树,那么每一个指针对应着字母表里的一个字母。从根节点开始,我们只要依次找到目标单词里下一个字母对应的指针,就可以一步步查找目标了。假设,我们要把字符串AB,ABBA,ABCD和BCD插入到Trie树中,由于Trie树的根节点不保存任何字母,我们从根节点的直接后继开始保存字母。如下图所示,我们在Trie树的第二层中保存了字母A和B,第三层中保存了B和C,其中B被标记为深蓝色表示单词AB已经插入完成。
图2 Trie树的实现
我们发现由于Trie的每个节点都有一个长度为26指针数组,但我们知道并不是每个指针数组都保存记录,空的指针数组导致内存空间的浪费。
假设,我们要设计一个翻译软件,翻译软件少不了查词功能,而且当用户输入要查询的词汇时,软件会提示相似单词,让用户选择要查询的词汇,这样用户就无需输入完整词汇就能进行查询,而且用户体验更好。
我们将使用Trie树结构存储和检索单词,从而实现词汇的智能提示功能,这里我们只考虑26英文字母匹配的实现,所以我们将构建一棵26叉树。
由于每个节点下一层都包含26个节点,那么我们在节点类中添加节点属性,节点类的具体实现如下:
/// <summary> /// The node type. /// Indicates the word completed or not. /// </summary> public enum NodeType { COMPLETED, UNCOMPLETED }; /// <summary> /// The tree node. /// </summary> public class Node { const int ALPHABET_SIZE = 26; internal char Word { get; set; } internal NodeType Type { get; set; } internal Node[] Child; /// <summary> /// Initializes a new instance of the <see cref="Node"/> class. /// </summary> /// <param name="word">The word.</param> /// <param name="nodeType">Type of the node.</param> public Node(char word, NodeType nodeType) { this.Word = word; this.Type = nodeType; this.Child = new Node[ALPHABET_SIZE]; } }
上面我们定义一个枚举类型NodeType,它用来标记词汇是否插入完成;接着,我们定义了一个节点类型Node,它包含两个属性Word和Type,Word用来保存当前节点的字母,Type用来标记当前节点是否插入完成。
接下来,我们要定义Trie树类型,并且添加Insert(),Find()和FindSimilar()方法。
/// <summary> /// The trie tree entity. /// </summary> public class Trie { const int ALPHABET_SIZE = 26; private Node _root; private HashSet<string> _hashSet; public Trie() { _root = CreateNode(' '); } public Node CreateNode(char word) { var node = new Node(word, NodeType.UNCOMPLETED); return node; } /// <summary> /// Inserts the specified node. /// </summary> /// <param name="node">The node.</param> /// <param name="word">The word need to insert.</param> private void Insert(ref Node node, string word) { Node temp = node; foreach (char t in word) { if (null == temp.Child[this.CharToIndex(t)]) { temp.Child[this.CharToIndex(t)] = this.CreateNode(t); } temp = temp.Child[this.CharToIndex(t)]; } temp.Type = NodeType.COMPLETED; } /// <summary> /// Inserts the specified word. /// </summary> /// <param name="word">Retrieval word.</param> public void Insert(string word) { if (string.IsNullOrEmpty(word)) { throw new ArgumentException("word"); } Insert(ref _root, word); } /// <summary> /// Finds the specified word. /// </summary> /// <param name="word">Retrieval word.</param> /// <returns>The tree node.</returns> public Node Find(string word) { if (string.IsNullOrEmpty(word)) { throw new ArgumentException("word"); } int i = 0; Node temp = _root; var words = new HashSet<string>(); while (i < word.Length) { if (null == temp.Child[this.CharToIndex(word[i])]) { return null; } temp = temp.Child[this.CharToIndex(word[i++])]; } if (temp != null && NodeType.COMPLETED == temp.Type) { _hashSet = new HashSet<string> { word }; return temp; } return null; } /// <summary> /// Finds the simlar word. /// </summary> /// <param name="word">The words have same prefix.</param> /// <returns>The collection of similar words.</returns> public HashSet<string> FindSimilar(string word) { Node node = Find(word); DFS(word, node); return _hashSet; } /// <summary> /// DFSs the specified prefix. /// </summary> /// <param name="prefix">Retrieval prefix.</param> /// <param name="node">The node.</param> private void DFS(string prefix, Node node) { for (int i = 0; i < ALPHABET_SIZE; i++) { if (node.Child[i] != null) { DFS(prefix + node.Child[i].Word, node.Child[i]); if (NodeType.COMPLETED == node.Child[i].Type) { _hashSet.Add(prefix + node.Child[i].Word); } } } } /// <summary> /// Converts char to index. /// </summary> /// <param name="ch">The char need to convert.</param> /// <returns>The index.</returns> private int CharToIndex(char ch) { return ch - 'a'; } }
上面我们,定义了Trie树类,它包含两个字段分别是:_root和_hashSet,_root用来保存Trie树的根节点,我们使用_hashSet保存前缀匹配的所有单词。
接着,我们在Trie树类中定义了CreateNode(),Insert(),Find(),FindSimilar()和DFS()等方法。
CreateNode()方法用来创建树的节点,Insert()方法把节点插入树中,Find()和FindSimilar()方法用来查找指定单词,DFS()方法是查找单词的具体实现,它通过深度搜索的方法遍历节点查找匹配的单词,最后把匹配的单词保存到_hashSet中。
接下来,我们创建一棵Trie树,然后把两千个英语单词插入到Trie树中,最后我们查找前缀为“the”的所有单词包括前缀本身。
public class Program { public static void Main() { // Creates a file object. var file = File.ReadAllLines(Environment.CurrentDirectory + "//1.txt"); // Creates a trie tree object. var trie = new Trie(); foreach (var item in file) { var sp = item.Split(new char[] { ' ' }, StringSplitOptions.RemoveEmptyEntries); // Inserts word into to the tree. trie.Insert(sp.LastOrDefault().ToLower()); ////ternaryTree.Insert(sp.LastOrDefault().ToLower()); } var similarWords = trie.FindSimilar("jk"); foreach (var similarWord in similarWords) { Console.WriteLine("Similar word: {0}", similarWord); } } }
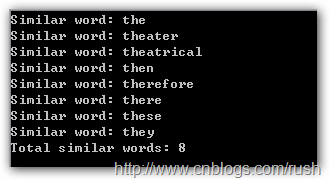
图3 匹配词结果
我们在1.txt文本文件中通过正则表达式(^:z the+)查找前缀为the的所有单词,恰好就是上面8个单词。
Ternary Tree的定义
前面,我们介绍了Trie树结构,它的实现简单但空间效率低。如果要支持26个英文字母,每个节点就要保存26个指针,假若我们还要支持国际字符、标点符号、区分大小写,内存用量就会急剧上升,以至于不可行。
由于节点数组中保存的空指针占用了太多内存,我们遇到的困难与此有关,因此可以考虑改用其他数据结构去代替,比如用hash map。然而,管理成千上万个hash map肯定也不是什么好主意,而且它使数据的相对顺序信息丢失,所以我们还是去看看另一种更好解法吧——Ternary Tree。
接下来,我们将介绍三叉搜索树,它结合字典树的时间效率和二叉搜索树的空间效率优点。
Ternary Tree的实现
三叉搜索树使用了一种聪明的手段去解决Trie的内存问题(空的指针数组)。为了避免多余的指针占用内存,每个Trie节点不再用数组来表示,而是表示成“树中有树”。Trie节点里每个非空指针都会在三叉搜索树里得到属于它自己的节点。
接下来,我们将实现三叉搜索树的节点类,具体实现如下:
/// <summary> /// The node type. /// Indicates the word completed or not. /// </summary> public enum NodeType { COMPLETED, UNCOMPLETED }; /// <summary> /// The tree node. /// </summary> public class Node { internal char Word { get; set; } internal Node LeftChild, CenterChild, RightChild; internal NodeType Type { get; set; } public Node(char ch, NodeType type) { Word = ch; Type = type; } }
由于三叉搜索树包含三种类型的箭头。第一种箭头和Trie里的箭头是一样的,也就是图2里画成虚线的向下的箭头。沿着向下箭头行进,就意味着“匹配上”了箭头起始端的字符。如果当前字符少于节点中的字符,会沿着节点向左查找,反之向右查找。
接下来,我们将定义Ternary Tree类型,并且添加Insert(),Find()和FindSimilar()方法。
/// <summary> /// The ternary tree. /// </summary> public class TernaryTree { private Node _root; ////private string _prefix; private HashSet<string> _hashSet; /// <summary> /// Inserts the word into the tree. /// </summary> /// <param name="s">The word need to insert.</param> /// <param name="index">The index of the word.</param> /// <param name="node">The tree node.</param> private void Insert(string s, int index, ref Node node) { if (null == node) { node = new Node(s[index], NodeType.UNCOMPLETED); } if (s[index] < node.Word) { Node leftChild = node.LeftChild; this.Insert(s, index, ref node.LeftChild); } else if (s[index] > node.Word) { Node rightChild = node.RightChild; this.Insert(s, index, ref node.RightChild); } else { if (index + 1 == s.Length) { node.Type = NodeType.COMPLETED; } else { Node centerChild = node.CenterChild; this.Insert(s, index + 1, ref node.CenterChild); } } } /// <summary> /// Inserts the word into the tree. /// </summary> /// <param name="s">The word need to insert.</param> public void Insert(string s) { if (string.IsNullOrEmpty(s)) { throw new ArgumentException("s"); } Insert(s, 0, ref _root); } /// <summary> /// Finds the specified world. /// </summary> /// <param name="s">The specified world</param> /// <returns>The corresponding tree node.</returns> public Node Find(string s) { if (string.IsNullOrEmpty(s)) { throw new ArgumentException("s"); } int pos = 0; Node node = _root; _hashSet = new HashSet<string>(); while (node != null) { if (s[pos] < node.Word) { node = node.LeftChild; } else if (s[pos] > node.Word) { node = node.RightChild; } else { if (++pos == s.Length) { _hashSet.Add(s); return node.CenterChild; } node = node.CenterChild; } } return null; } /// <summary> /// Get the world by dfs. /// </summary> /// <param name="prefix">The prefix of world.</param> /// <param name="node">The tree node.</param> private void DFS(string prefix, Node node) { if (node != null) { if (NodeType.COMPLETED == node.Type) { _hashSet.Add(prefix + node.Word); } DFS(prefix, node.LeftChild); DFS(prefix + node.Word, node.CenterChild); DFS(prefix, node.RightChild); } } /// <summary> /// Finds the similar world. /// </summary> /// <param name="s">The prefix of the world.</param> /// <returns>The world has the same prefix.</returns> public HashSet<string> FindSimilar(string s) { Node node = this.Find(s); this.DFS(s, node); return _hashSet; } }
和Trie类似,我们在TernaryTree 类中,定义了Insert(),Find()和FindSimilar()方法,它包含两个字段分别是:_root和_hashSet,_root用来保存Trie树的根节点,我们使用_hashSet保存前缀匹配的所有单词。
由于三叉搜索树每个节点只有三个叉,所以我们在进行节点插入操作时,只需判断插入的字符与当前节点的关系(少于,等于或大于)插入到相应的节点就OK了。
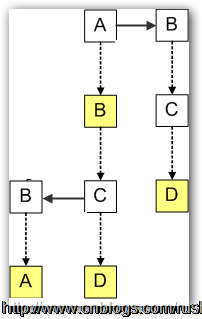
我们使用之前的例子,把字符串AB,ABBA,ABCD和BCD插入到三叉搜索树中,首先往树中插入了字符串AB,接着我们插入字符串ABCD,由于ABCD与AB有相同的前缀AB,所以C节点都是存储到B的CenterChild中,D存储到C的CenterChild中;当插入ABBA时,由于ABBA与AB有相同的前缀AB,而B字符少于字符C,所以B存储到C的LeftChild中;当插入BCD时,由于字符B大于字符A,所以B存储到C的RightChild中。
图4三叉搜索树
我们注意到插入字符串的顺序会影响三叉搜索树的结构,为了取得最佳性能,字符串应该以随机的顺序插入到三叉树搜索树中,尤其不应该按字母顺序插入,否则对应于单个Trie
节点的子树会退化成链表,极大地增加查找成本。当然我们还可以采用一些方法来实现自平衡的三叉树。
由于树是否平衡取决于单词的读入顺序,如果按排序后的顺序插入,则该方式生成的树是最不平衡的。单词的读入顺序对于创建平衡的三叉搜索树很重要,所以我们通过选择一个排序后数据集合的中间值,并把它作为开始节点,通过不断折半插入中间值,我们就可以创建一棵平衡的三叉树。我们将通过方法BalancedData()实现数据折半插入,具体实现如下:
/// <summary> /// Balances the ternary tree input data. /// </summary> /// <param name="file">The file saves balanced data.</param> /// <param name="orderList">The order data list.</param> /// <param name="offSet">The offset.</param> /// <param name="len">The length of data list.</param> public void BalancedData(StreamWriter file, IList<KeyValuePair<int, string>> orderList, int offSet, int len) { if (len < 1) { return; } int midLen = len >> 1; // Write balanced data into file. file.WriteLine(orderList[midLen + offSet].Key + " " + orderList[midLen + offSet].Value); BalancedData(file, orderList, offSet, midLen); BalancedData(file, orderList, offSet + midLen + 1, len - midLen - 1); }
上面,我们定义了方法BalancedData(),它包含四个参数分别是:file,orderList,offSet和len。File写入平衡排序后的数据到文本文件。orderList按顺序排序后的数据。offSet偏移量。Len插入的数据量。
同样我们创建一棵三叉搜索树,然后把两千个英语单词插入到三叉搜索树中,最后我们查找前缀为“ab”的所有单词包括前缀本身。
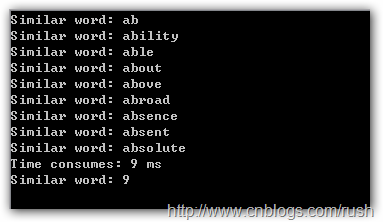
public class Program { public static void Main() { // Creates a file object. var file = File.ReadAllLines(Environment.CurrentDirectory + "//1.txt"); // Creates a trie tree object. var ternaryTree = new TernaryTree(); var dictionary = new Dictionary<int, string>(); foreach (var item in file) { var sp = item.Split(new char[] { ' ' }, StringSplitOptions.RemoveEmptyEntries); ternaryTree.Insert(sp.LastOrDefault().ToLower()); } Stopwatch watch = Stopwatch.StartNew(); // Gets words have the same prefix. var similarWords = ternaryTree.FindSimilar("ab"); foreach (var similarWord in similarWords) { Console.WriteLine("Similar word: {0}", similarWord); } watch.Stop(); Console.WriteLine("Time consumes: {0} ms", watch.ElapsedMilliseconds); Console.WriteLine("Similar word: {0}", similarWords.Count); Console.Read(); } }
图5匹配结果
我们在1.txt文本文件中通过正则表达式(^:z ab+)查找前缀为ab的所有单词,刚好就是上面9个单词。
Ternary Tree的应用
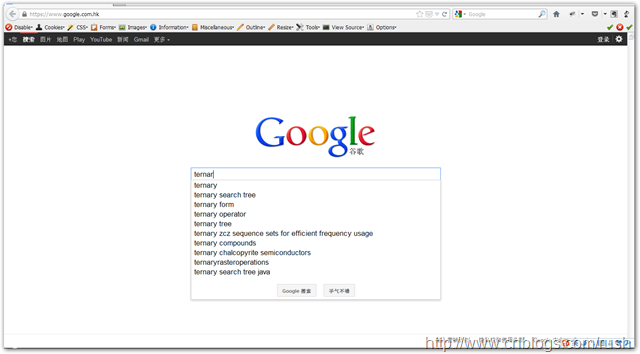
我们使用搜索引擎进行搜索时,它会提供自动完成(Auto-complete)功能,让用户更加容易查找到相关的信息;假如:我们在Google中输入ternar,它会提示与ternar的相关搜索信息。
图6 Auto-complete功能
Google根据我们的输入ternar,提示了ternary,ternary search tree等等搜索信息,自动完成(Auto-complete)功能的实现的核心思想三叉搜索树。
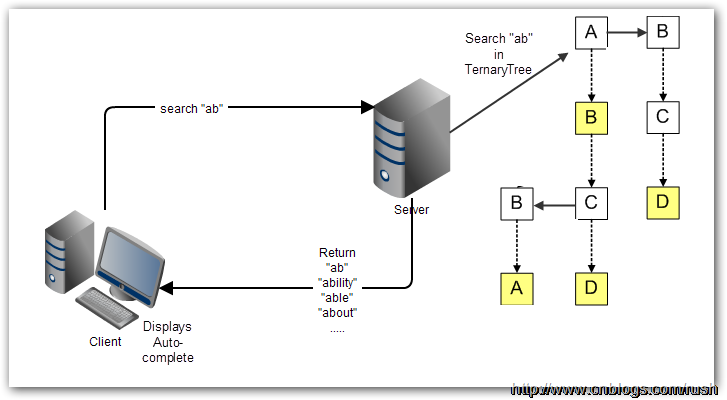
对于Web应用程序来说,自动完成(Auto-complete)的繁重处理工作绝大部分要交给服务器去完成。很多时候,自动完成(Auto-complete)的备选项数目巨大,不适宜一下子全都下载到客户端。相反,三叉树搜索是保存在服务器上的,客户端把用户已经输入的单词前缀送到服务器上作查询,然后服务器根据三叉搜索树算法获取相应数据列表,最后把候选的数据列表返回给客户端。
图7 Auto-complete功能
1.1.3 总结
Trie树是一种非常重要的数据结构,它在信息检索,字符串匹配等领域有广泛的应用,同时,它也是很多算法和复杂数据结构的基础,如后缀树,AC自动机等;三叉搜索树是结合了数字搜索树的时间效率和二叉搜索树的空间效率优点,而且它有效的避免了Trie空指针数据的空间浪费问题。
树是否平衡取决于单词的读入顺序。如果字符串经过排序后的顺序插入,则该树是最不平衡的,由于对应于单个Trie节点的子树会退化成链表,极大地增加查找成本。
最后,祝大家新年快乐,身体健康,工作愉快和Code With Pleasant,By Jackson Huang。