0.1 分类
非线性时间比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此称为非线性时间比较类排序。
线性时间非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此称为线性时间非比较类排序。


0.3 相关概念
稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
时间复杂度:对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
空间复杂度:是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。
一、冒泡排序
从左向右依次比较相邻两个数,找出大的后移。
第一轮,找出最大的放到最后一位;
第二轮,找出次大的放到倒数第二位;
多次循环后,排序完成。
二、选择排序(Selection Sort)
首先选择所有数据中最小的,放到第一位;然后再剩下的数据中选择次小的,放到第二位;…多次循环后,排序完成。
(比较冒泡和选择,冒泡两个数值比较完后,就得交换两个数值;选择排序的话,比较只需记录最小的下标,全部完后再交换)
三、插入排序(Insertion Sort)
假设第一个值最小,第二个值 与第一个值比较,如果小于第一个值,则插入到第一个值之前,这样,前两个值就排好序了。
然后,第三个值与排好序的前两个值比较,在合适的位置插入进去,这样前三个值就排好序了。
依次类推。排好所有的值。
难点:排好序的值得统一右移,通过while来实现比较好。
function insertionSort(arr) {
var len = arr.length;
var preIndex, current;
for (var i = 1; i < len; i++) {
preIndex = i - 1;
current = arr[i];
while (preIndex >= 0 && arr[preIndex] > current) {
arr[preIndex + 1] = arr[preIndex];
preIndex--;
}
arr[preIndex + 1] = current;
}
return arr;
}
黄色部分,通过arr[preIndex]>current,来控制条件,通过preIndex--来控制下标。
四、希尔排序(Shell Sort)
1959年Shell发明,第一个突破O(n2)的排序算法,是简单插入排序的改进版。它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。

利用局部先排序,然后最后插入的时候,比较次数会比一开始就采用插入排序要少的方法。
#include <iostream>
using namespace std;
void ShellSort(int *a,int len) //数组的位置引用
{
int i, j, h;
int r, temp;
int x = 0;
for (r=len/2;r>=1;r/=2) //r>=1保证至少有两个可以比较的数,r/=2确定序列对
{
for (i=r;i<len;i++)
{
temp = a[i];
j = i - r; //分组方式
while (j>=0 && temp<a[j])//对配对的两个数进行比较
{
a[j + r] = a[j]; //向右移
j -= r;
}
a[j + r] = temp; //插入
}
x++; //第几步
cout<<"第"<<x<<"步的排序结果:";
for (h=0;h<len;h++)
{
cout<<a[h]<<" ";
}
cout<<"
";
}
}
int main()
{
int i;
int arr[] = {50,83,88,87,61,84,70,60,80,99};
cout<<"排序前:"<<"
";
for (i=0;i<10;i++)
{
cout<<arr[i]<<' ';
}
cout<<"
";
ShellSort(arr,10); //注意引用方式
cout<<"排序后:"<<"
";
for (i=0;i<10;i++)
{
cout<<arr[i]<<' ';
}
cout<<"
";
return 0;
}
(1)
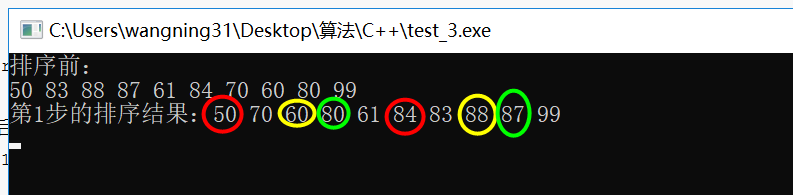
交换的是相同颜色的,也就是相同颜色的是一个组,此时增量为5,分为了5组。
(2)
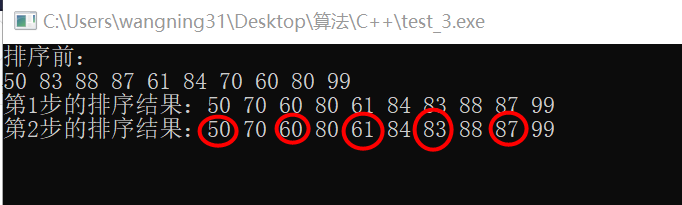
相同颜色的为一组,排序;增量为2,分为了2组。
(3)
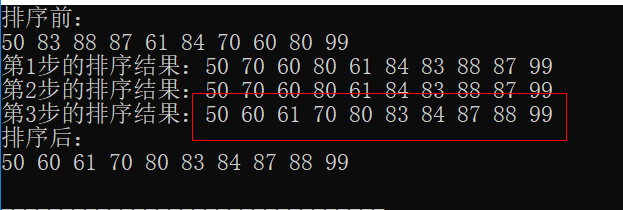
增量为1,分为1组,采用插入排序。
五、