MATLAB 随机过程基本理论

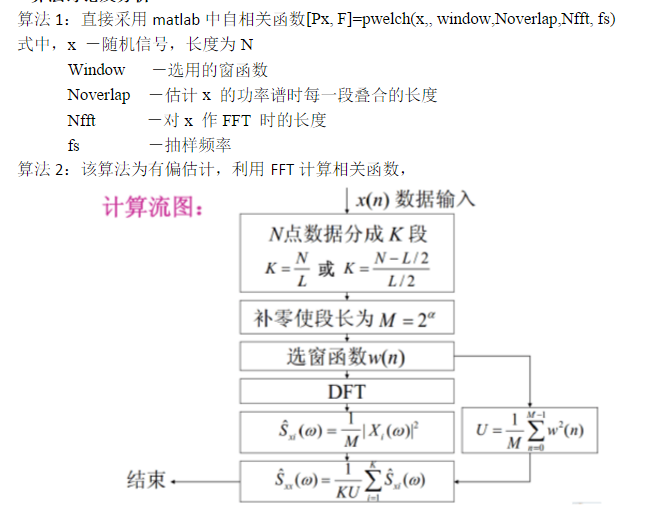
一、平稳随机过程

1、严平稳随机过程

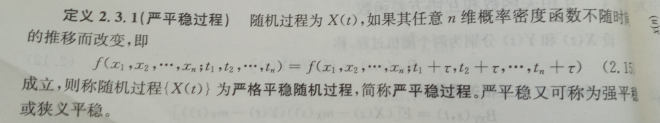
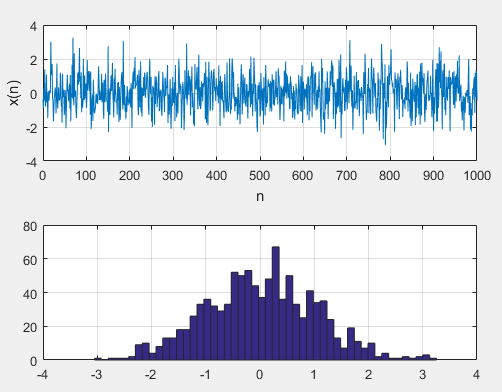
clc
clear

n=0:1000;
x=randn(1,1001);
subplot(211),plot(n,x);
xlabel('n');ylabel('x(n)');
grid on
subplot(212),hist(x,50)
grid on

2、

 3、随机相位正弦信号

3.1

%随机相位正弦信号
clc
clear
t=0:0.01:30;
w=pi/2;
x1=cos(w*t+2*pi*rand*ones(1,3001));
x2=cos(w*t+2*pi*rand*ones(1,3001));
x3=cos(w*t+2*pi*ones(1,3001));
plot(t,x1,'-.',t,x2,'--',t,x3,'-');
xlabel('n');ylabel('x(n)');
grid on
legend('样本1','样本2','样本3')

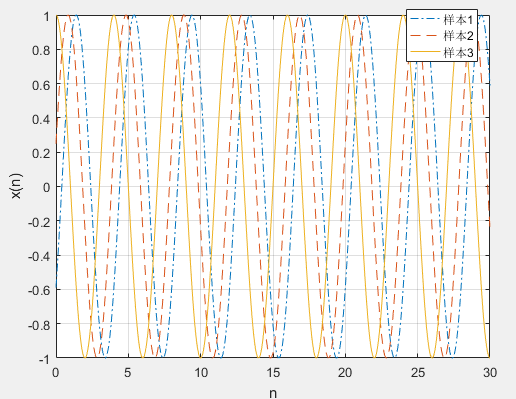
样本1和样本2的初始相位是随机生成的，样本3的初始相位为定值：2*pi。

注意一个信号只有一个初始相位，而不是说一个点一个初始相位

3.2 随机相位正弦信号均值

clc
clear
t=0:0.01:30;
N=10000;
w=2*pi;
y=zeros(1,3001);
for ii=1:N
    x=cos(w*t+2*pi*rand*ones(1,3001));
    y=y+x;
end
y_mean=y/N;%集平均

plot(t,y_mean,'-');
xlabel('n');ylabel('E[X(t)]');
grid on

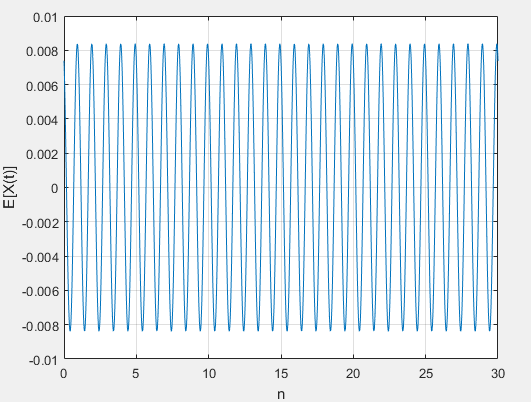
可以看出1、振幅和角频率相同而初始相位不相同的正弦信号叠加还是同频率的正弦信号，只是初始相位和幅值发生了变化2、随机相位正弦信号的均值为0。

 

3.3 随机相位正弦信号自相关函数

clc
clear
tao=-5:0.01:5;%时间差
t=1; %选取一个时间点
N=10000;%仿真次数
w=2*pi;%角频率
y=0;
for ii=1:N
    fai=rand;%随机相位
    x=cos(w*t+w*fai).*cos(w*t+w*tao+w*fai);%自相关函数，改变时间差
    y=y+x;
end
y_mean=y/N;%求平均值

plot(tao,y_mean,'-');
xlabel('tao');ylabel('Rx(tao)');
grid on

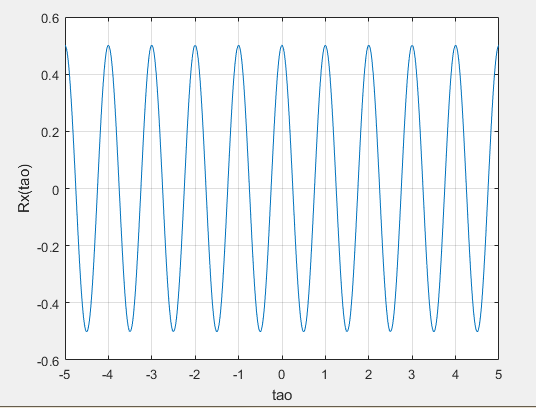
更改时间点

clc
clear
tao=-5:0.01:5;%时间差
t=1.5; %选取一个时间点
N=10000;%仿真次数
w=2*pi;%角频率
y=0;
for ii=1:N
    fai=rand;%随机相位
    x=cos(w*t+w*fai).*cos(w*t+w*tao+w*fai);%自相关函数，改变时间差
    y=y+x;
end
y_mean=y/N;%求平均值，循环10000次，求出一个点的一个值

plot(tao,y_mean,'-');
xlabel('tao');ylabel('Rx(tao)');
grid on

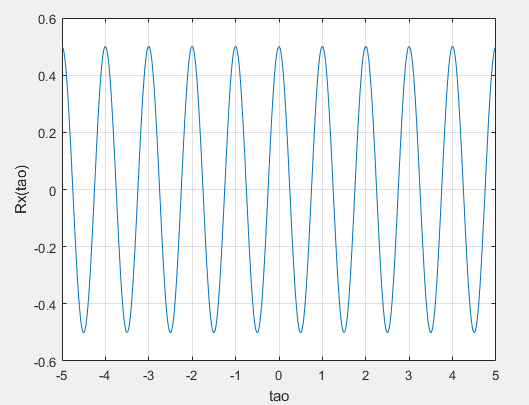
时间点更改为1.5后，自相关函数没有改变，也就证明了E[cos(wt+fai)*cos(w(t+tao)+fai)]的图形与t无关，仅仅与tao有关。

4、宽平稳过程的均方遍历性

 从这可以看出时间均值和集均值的差异。时间均值是一个随机函数各个值平均，类似于一个人五门课的平均分。而集平均，是指多个随机信号的平均值，类似于全班同学的平均分。

4.1 时间平均

clear all
clc
t=0:0.01:1000; %选取一个时间点
w=2*pi;%角频率
x=cos(w*t+2*pi*rand*ones(1,100001));%初始相位一直是定值
plot(t(1:500),x(1:500))
grid
Ex=mean(x') %时间平均值

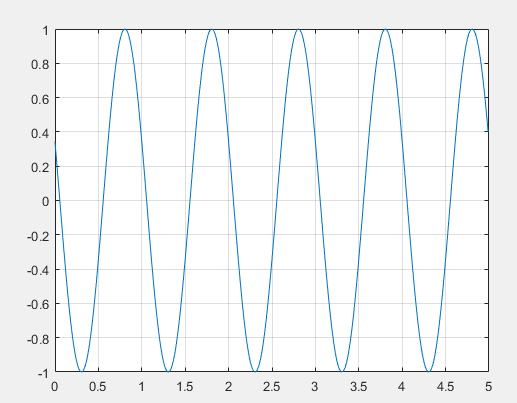
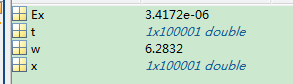
可以看出时间均值和集均值都是约等于0。

4.2 自相关函数的时间平均和集平均

clc
clear
corr=[];
w=2*pi;%角频率
a=rand;
for tao=-5:0.01:5
    t=0:0.01:1000;
    x=cos(w*t+w*a*ones(1,100001)).*cos(w*t+w*tao+w*a);%自相关函数，改变时间差
    corr_mean=mean(x');
    corr=cat(1,corr,corr_mean);%将值连接起来到一个矩阵里，求出对应tao的值
end
tao=-5:0.01:5
plot(tao,corr,'-');
xlabel('tao');ylabel('corr');
grid on

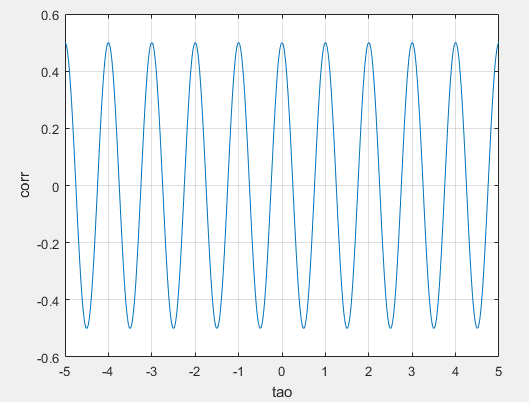
自相关的时间平均和集平均相等。

所以随机相位正弦信号具有各态历经性。

二、随机信号谱分析

通过傅里叶分析来研究频域特性就是功率谱分析

1、连续周期傅里叶级数

程序实现

clc
clear
t=-2:0.0001:2;
omega=2*pi;
y=square(2*pi*t,50);%周期为1的防波信号
n_max=[1,5,20,100];
for k=1:4
    fk=zeros(1,length(t));
    for n=1:2:n_max(k)
        bn=4/(pi*n);%系数
        fk=fk+bn*sin(n*omega*t);%公式
    end
    subplot(2,2,k)
    plot(t,y,t,fk,'linewidth',1.5);
    xlabel('t(sec)');ylabel('部分和波形');
    String=['最大谐波数=',num2str(n_max(k))];
    axis([-2 2 -3 3]);
    grid on;
    title(String);
    disp([String,'时，在信号跳变点附近过冲幅度（ %）']);%注意连接情况
    f_max=(max(fk)-max(y))*100%谐波最大值减去方波最大值
end

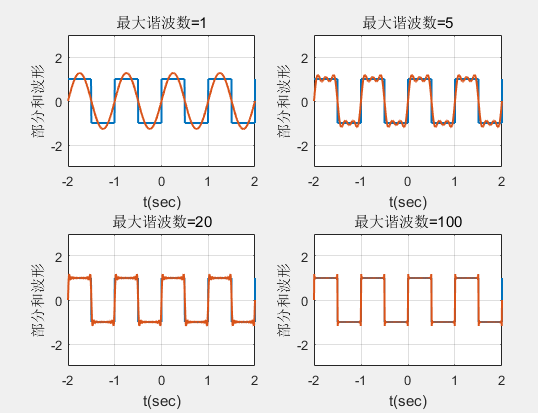
当谐波数分别为1、5、20、100时，在信号跳变点附近的过冲幅度分别为27.320%、18.8357%、17.9814%、17.9013%，这就是著名的Gibbs现象。该现象在一般情形下都会发生，不仅仅限于周期性方波。

将具有不连续点的周期函数（如矩形脉冲)进行傅立叶级数展开后，选取有限项进行合成。当选取的项数越多，在所合成的波形中出现的峰起越靠近原信号的不连续点。当选取的项数很大时，该峰起值趋于一个常数，大约等于总跳变值的9%。这种现象称为吉布斯效应。

2、离散周期，连续非周期，离散非周期

3、功率谱密度

 

 

 随机过程的功率谱密度与确定信号频谱密度对应，不包含任何相位信息，这是由随机信号的随机性决定的。

自相关函数从时域描述随机信号，而功率谱密度从频域描述随机信号

三、随机信号自相关函数估计

3.1直接估计法

%64个标准正态分布的自相关函数有偏和无偏估计
clc
clear
N=64;
x=randn(1,N);
Rx1=xcorr(x,'unbiased');
Rx2=xcorr(x,'biased');
m=(-N+1):(N-1);
plot(m,Rx1,'r--');
hold on
plot(m,Rx2);
xlabel('m');ylabel('Rx');
axis([-N+1 N-1 -1 1.5]);
grid on;
legend('无偏估计','有偏估计');

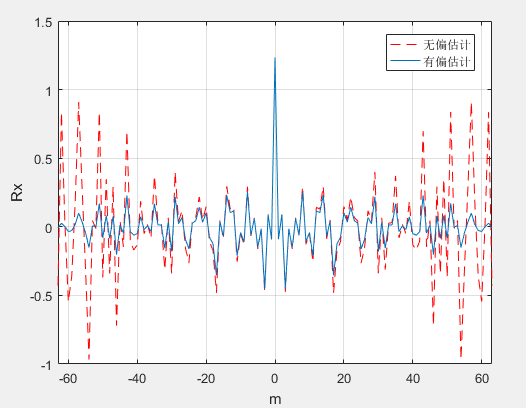
可以看出当m比较小时，两者几乎一致；m变大时，差异明显；关于m=0对称。

2、快速傅里叶变换

clear all
clear
x=1:5;
y=reshape(1:25,5,5)
plot(x,y)

plot画图方法，按列开始画的。矩阵画法。

　　

（1）正态分布的自相关函数

%4096点个标准正态分布的自相关函数xcorr和FFT方法比较
clc
clear
N=4096;
x=randn(1,N);

tic
Rx1=xcorr(x,'biased');
time1=toc
m=(-N+1):(N-1);%个苏
subplot(121)
plot(m,Rx1);
xlabel('m');ylabel('Rx1');
axis([-N+1 N-1 -1 1.5]);
grid on;
title('xcorr命令法');


tic
Xk=fft(x,2*N);
Rx2=ifft(abs(Xk).^2/N);
time2=toc
m=(-N):(N-1);%注意变化后的个数
subplot(122)
plot(m,fftshift(Rx2));%注意 fftshift的使用
xlabel('m');ylabel('Rx2');

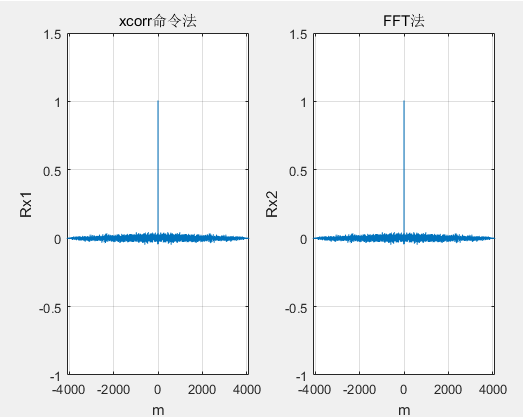
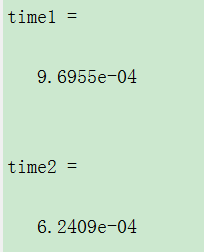
时间FFT方法要花费少。

FFT方法比xcorr命令方法多一个点。

（2）余弦的自相关函数

clc
clear

t=1:0.001:20;
N=length(t);
x=cos(2*pi*t);

tic
Rx1=xcorr(x,'biased');
time1=toc
m=(-N+1):(N-1);
subplot(121)
plot(m,Rx1);
xlabel('m');ylabel('Rx1');
%axis([-N+1 N-1 -1 1.5]);
grid on;
title('xcorr命令法');


tic
Xk=fft(x,2*N);
Rx2=ifft(abs(Xk).^2/N);
time2=toc
m=(-N):(N-1);
subplot(122)
plot(m,fftshift(Rx2));
xlabel('m');ylabel('Rx2');
%axis([-N+1 N-1 -1 1.5]);
grid on;
title('FFT法');

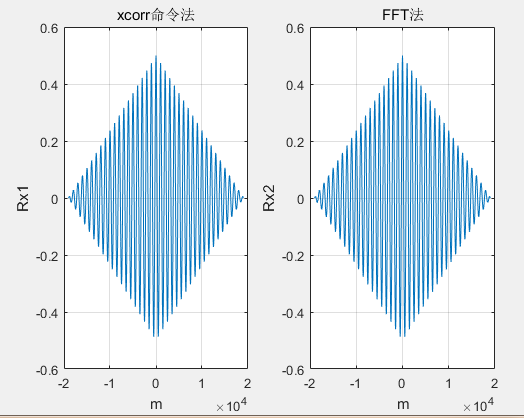
（3）随机信号与高斯白噪声信号叠加

%随机相位正弦信号与高斯白噪声信号的叠加
clc
clear

N=1024;%点数，一个信号采样点
n=32;%信号数
t=0:N-1;
m=-N:N-1;
x1n=random('norm',0,1,N,n);%N行，n列的数，高斯白噪声
% x1k=fft(x1n,2*N);%2n行，32列
% R1x=ifft((abs(x1k).^2)/N);%2n行，32列
A=random('unif',0,1,1,32)*2*pi;%32个[0,2*pi]随机相位
for k=1:n
    x2n(:,k)=cos(2*pi*4*t(:)/N+A(k));%n个相位，随机相位正弦信号，除以N是为了使周期个数变小，只有四个周期。
    xn(:,k)=x1n(:,k)+x2n(:,k);%叠加信号
end

subplot(321)
plot(t,x1n(:,1));
xlabel('m');ylabel('Rn(m)');
axis([0 N -5 5]);
title('一个高斯白噪声')
grid on;

subplot(322)
plot(t,x1n);
xlabel('m');ylabel('Rn(m)');
axis([0 N -5 5]);
title([num2str(n),'个高斯白噪声'])
grid on;

subplot(323)
plot(t,x2n(:,1));
xlabel('m');ylabel('Rn(m)');
axis([0 N -2 2]);
title('一个随机相位正弦信号')
grid on;

subplot(324)
plot(t,x2n);
xlabel('m');ylabel('Rn(m)');
axis([0 N -2 2]);
title([num2str(n),'个随机相位正弦信号'])
grid on;

subplot(325)
plot(t,xn(:,1));
xlabel('m');ylabel('Rn(m)');
axis([0 N -5 5]);
title('一个叠加信号')
grid on;

subplot(326)
plot(t,xn);
xlabel('m');ylabel('Rn(m)');
axis([0 N -5 5]);
title([num2str(n),'个叠加信号'])
grid on;

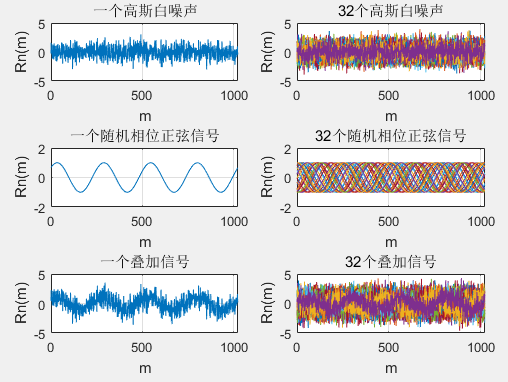
可以看出来，时域展示叠加信号时，混乱，找不出规律

　

%随机相位正弦信号与高斯白噪声信号的叠加
clc
clear

N=1024;%点数，一个信号采样点
n=32;%信号数
t=0:N-1;
m=-N:N-1;
x1n=random('norm',0,1,N,n);%N行，n列的数，高斯白噪声
x1k=fft(x1n,2*N);%2n行，32列
R1x=ifft((abs(x1k).^2)/N);%2n行，32列
A=random('unif',0,1,1,32)*2*pi;%32个[0,2*pi]随机相位
for k=1:n
    x2n(:,k)=cos(2*pi*4*t(:)/N+A(k));%n个相位，随机相位正弦信号
    xn(:,k)=x1n(:,k)+x2n(:,k);%叠加信号
end
x2k=fft(x2n,2*N);%2n行，32列
R2x=ifft((abs(x2k).^2)/N);%2n行，32列
xk=fft(xn,2*N);%2n行，32列
Rx=ifft((abs(xk).^2)/N);%2n行，32列

subplot(321)
plot(m,fftshift(R1x(:,1)));
xlabel('m');ylabel('Rn(m)');
axis([-N N-1 -1 1.5]);
title('一个高斯白噪声自相关')
grid on;

subplot(322)
plot(m,fftshift(R1x));
xlabel('m');ylabel('Rn(m)');
axis([-N N-1 -1 1.5]);
title([num2str(n),'个高斯白噪声自相关'])
grid on;

subplot(323)
plot(m,fftshift(R2x(:,1)));
xlabel('m');ylabel('Rn(m)');
axis([-N N-1 -1 1.5]);
title('一个随机相位正弦信号自相关')
grid on;

subplot(324)
plot(m,fftshift(R2x));
xlabel('m');ylabel('Rn(m)');
axis([-N N-1 -1 1.5]);
title([num2str(n),'个随机相位正弦信号自相关'])
grid on;

subplot(325)
plot(m,fftshift(Rx(:,1)));
xlabel('m');ylabel('Rn(m)');
axis([-N N-1 -1 2]);
title('一个叠加信号自相关')
grid on;

subplot(326)
plot(m,fftshift(Rx));
xlabel('m');ylabel('Rn(m)');
axis([-N N-1 -1 2]);
title([num2str(n),'个叠加信号自相关'])
grid on;

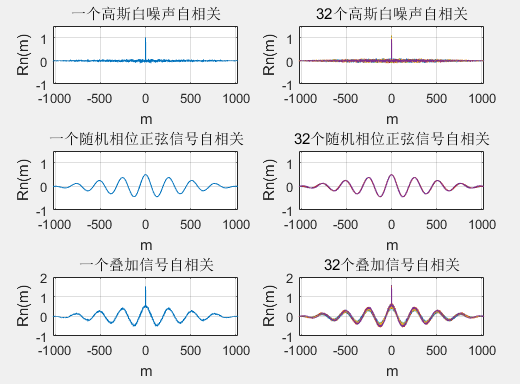
高斯白噪声仅仅在m=0时取得最大值，其他点很小。随机相位正弦信号的自相关基本符合正弦信号外形。合成信号时的自相关是两个分量自相关的相加。

四、平稳信号的谱估计

1、直接法——周期图法

（1）FFT方法

直接法又称周期图法，它是把随机序列x(n)的N个观测数据视为一能量有限的序列，直接计算x(n)的离散傅立叶变换，得X(k)，然后再取其幅值的平方，并除以N，作为序列x(n)真实功率谱的估计。

当采样频率fs.max大于信号中最高频率fmax的2倍时(fs.max>2fmax)，采样之后的数字信号完整地保留了原始信号中的信息，一般实际应用中保证采样频率为信号最高频率的2.56～4倍；采样定理又称奈奎斯特定理。

clc
clear

N=1024;%采样点数
fs=1000;%采样频率，满足采样定理
t=(0:N-1)/fs;%时间，平分了1024份。（0~1.24s）
fai=random('unif',0,1,1,2)*2*pi;%两个相位
A=[1,2];%两个振幅
f=[30,70];%两个频率，可以计算出信号周期
x=A(1)*cos(2*pi*f(1)*t+fai(1))+A(2)*cos(2*pi*f(2)*t+fai(2))+randn(size(t));%该信号
Sx=(abs(fft(x)).^2)/N;%功率谱密度公式

f=(0:N/2-1)*fs/N;%频率范围（一半）
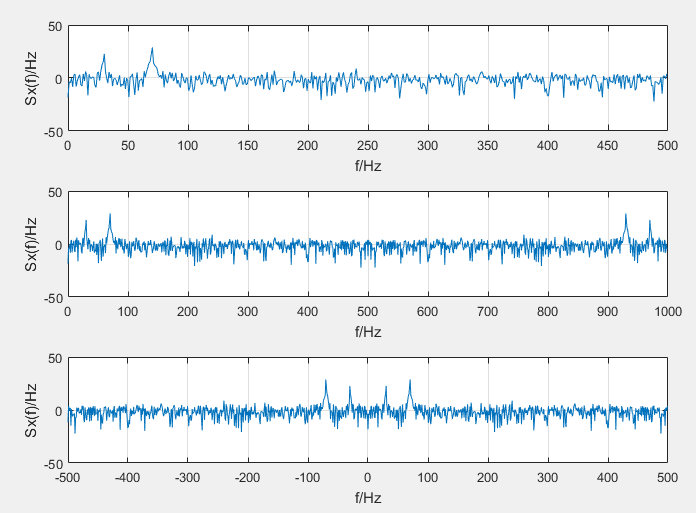
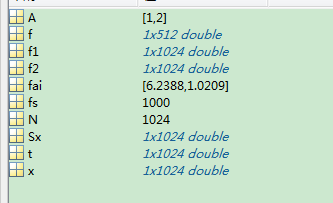
subplot(311),plot(f,10*log10(Sx(1:N/2)));%化为dB表示
xlabel('f/Hz');ylabel('Sx(f)/Hz');
grid on

f1=(0:N-1)*fs/N;%频率范围（正方向）
subplot(312),plot(f1,10*log10(Sx));%化为dB表示%频率和幅值不对应
xlabel('f/Hz');ylabel('Sx(f)/Hz');
grid on

f2=(-N/2:(N-2)/2)*fs/N;%频率范围（正方向）
subplot(313),plot(f2,fftshift(10*log10(Sx)));%化为dB表示%频率和幅值对应
xlabel('f/Hz');ylabel('Sx(f)/Hz');
grid on

close all
clc
clear
N=1024;
fs=1000;
t=(0:N-1)/fs;
fai=random('unif',0,1,1,2)*2*pi;
A=[1,2];
f=[30;70];
x=A*cos(2*pi*f*t+(fai)'*t)+randn(size(t));%利用矩阵乘法，简化了信号叠加的写法
Sx=(abs(fft(x)).^2)/N;
f=(0:N/2-1)*fs/N;
plot(f,10*log10(Sx(1:N/2)));
xlabel('f/Hz');ylabel('Sx(f)/Hz');
grid on

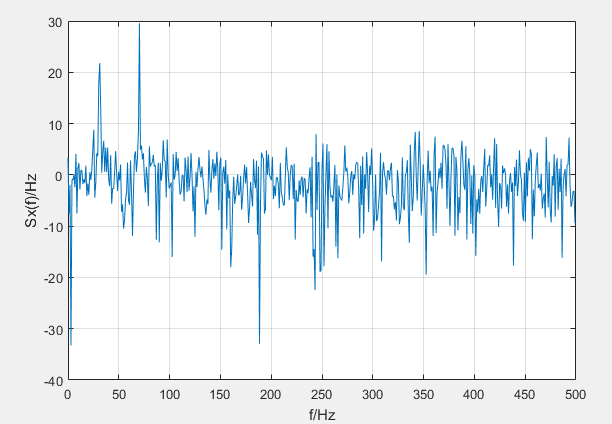
 直接用傅里叶变换公式推导的话得到的是双边谱，既-fs——fs,在matlab中用FFT得到的是单边谱，既0——2fs,因为在FFT之后我们得到的是一组复数，需要做abs。乘以2是因为我们的分析频率在0——fs,具体为什么除以点数N，在索引中有详细解释。

（2） periodogram方法

周期图法估计功率谱MATLAB命令为periodogram.

Pxx=periodogram(X)。返回随机序列组成的向量X的功率谱密度，X用与其长度相等的矩形窗。对于实信号，默认返回单边功率谱，复信号，返回双边谱

clear all
clear

N=1024;%采样点数
fs=1000;%采样频率，满足采样定理
t=(0:N-1)/fs;%时间，平分了1024份。（0~1.24s）
fai=random('unif',0,1,1,2)*2*pi;%两个相位
A=[1,2];%两个振幅
f=[30,70];%两个频率，可以计算出信号周期
x=A(1)*cos(2*pi*f(1)*t+fai(1))+A(2)*cos(2*pi*f(2)*t+fai(2))+randn(size(t));%该信号
Px=periodogram(x);
f=(0:N/2)*fs/N;%频率范围（一半）
plot(f,10*log10(Px));
xlabel('f/Hz');ylabel('Px(f)/Hz');
title('periodogram法')
grid on 

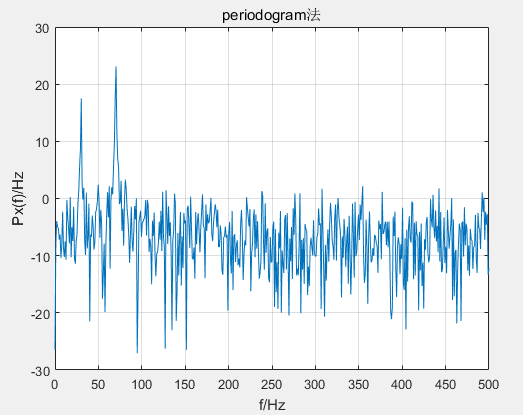
可以看到Px只有513个数据，返回的是单边谱。

clear all
clear

N=1024;%采样点数
fs=1000;%采样频率，满足采样定理
t=(0:N-1)/fs;%时间，平分了1024份。（0~1.24s）
fai=random('unif',0,1,1,2)*2*pi;%两个相位
A=[1,2];%两个振幅
f=[30,70];%两个频率，可以计算出信号周期
x=A(1)*cos(2*pi*f(1)*t+fai(1))+A(2)*cos(2*pi*f(2)*t+fai(2))+randn(size(t));%该信号

Px=periodogram(x);
f=(0:N/2)*fs/N;%频率范围（一半）
subplot(211),plot(f,10*log10(Px));
xlabel('f/Hz');ylabel('Px(f)/Hz');
title('periodogram法功率谱估计')
grid on

Sx=(abs(fft(x)).^2)/N;%功率谱密度公式
f=(0:N/2-1)*fs/N;%频率范围（一半）
subplot(212),plot(f,10*log10(Sx(1:N/2)));%化为dB表示
xlabel('f/Hz');ylabel('Sx(f)/Hz');
title('FFT法功率谱估计')
grid on　

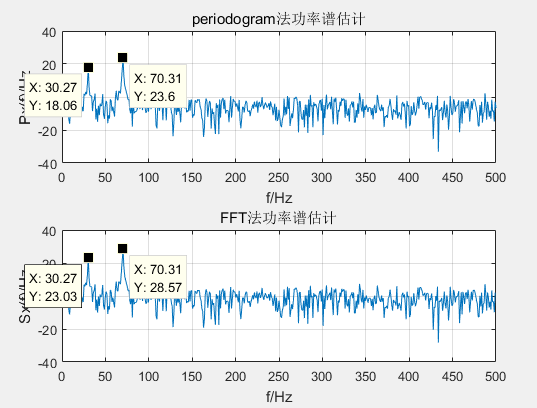
两种方法计算出来的数值有差异。具体差异可以参见：http://cn.mathworks.com/help/signal/ug/power-spectral-density-estimates-using-fft.html;jsessionid=3e406929b1cfa28e576c6818960d和http://www.ilovematlab.cn/thread-173424-2-1.html

（3）

clear all
clear
%多次频率谱估计平均
N=1024;%采样点数
fs=1000;%采样频率，满足采样定理
M=20;%估计次数
t=(0:N-1)/fs;%时间
fai=random('unif',0,1,1,M)*2*pi;%M个相位
x1=random('norm',0,1,N,M);
A=[1,2];%两个振幅
f=[30,70];%两个频率，可以计算出信号周期

for ii=1:M
    x(:,ii)=A(1)*cos(2*pi*f(1)*t(:)+fai(ii))+A(2)*cos(2*pi*f(2)*t(:)+fai(ii))+x1(:,ii);%该信号
    Px(:,ii)=periodogram(x(:,ii));
end
f=(0:N/2)*fs/N;%频率范围（一半）
subplot(121),plot(f,10*log10(Px));
xlabel('f/Hz');ylabel('Px(f)(dB/Hz)');
grid on
title('periodogram法功率谱估计')

EPx=mean(Px,2)
subplot(122),plot(f,10*log10(EPx));
xlabel('f/Hz');ylabel('EPx(f)/Hz');
title('periodogram法功率谱估计平均值')
grid on　　

 

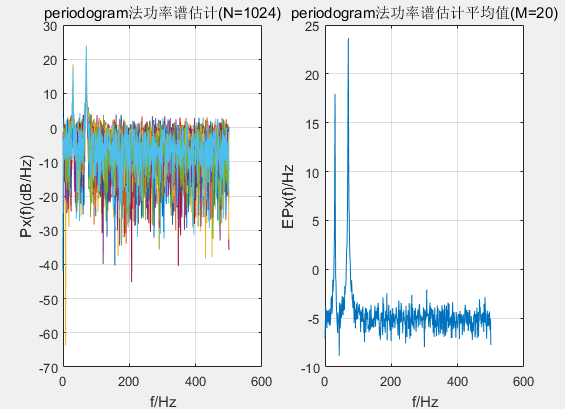
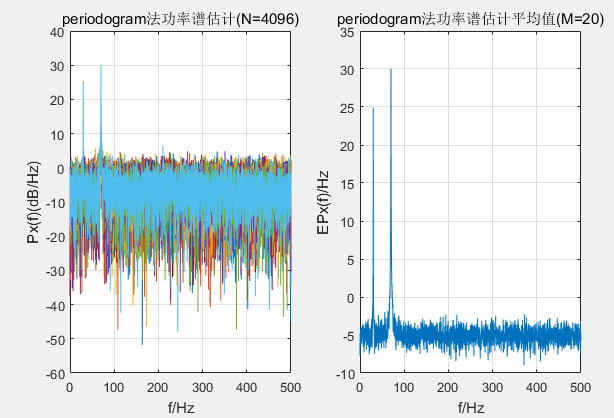
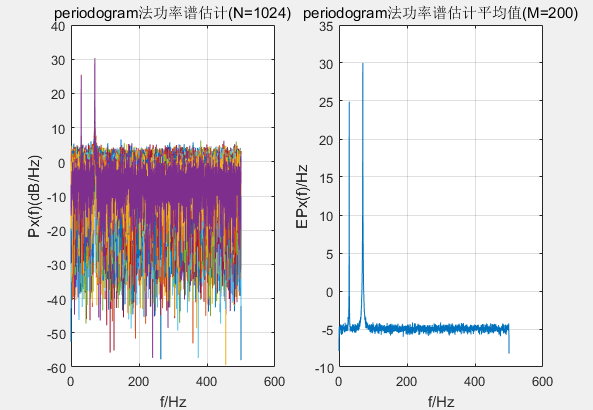
可以看出提高采样点数，可以提高频率分辨率；利用平均，可以降低功率谱方差。

 2、间接法——自相关函数法

clear all
clear

N=1024;%采样点数
fs=1000;%采样频率，满足采样定理
t=(0:N-1)/fs;%时间，平分了1024份。（0~1.24s）
fai=random('unif',0,1,1,2)*2*pi;%两个相位
A=[1,2];%两个振幅
f=[30,70];%两个频率，可以计算出信号周期
x=A(1)*cos(2*pi*f(1)*t+fai(1))+A(2)*cos(2*pi*f(2)*t+fai(2))+randn(size(t));%该信号

Rx=xcorr(x,'biased');自相关函数
Sx=abs(fft(Rx));
f=(0:N/2)*fs/N;%频率范围（一半）
plot(f,10*log10(Sx(1:N/2+1)));
xlabel('f/Hz');ylabel('Sx(f)(dB/Hz)');
title('自相关法求功率谱(N=1024)')
grid on 

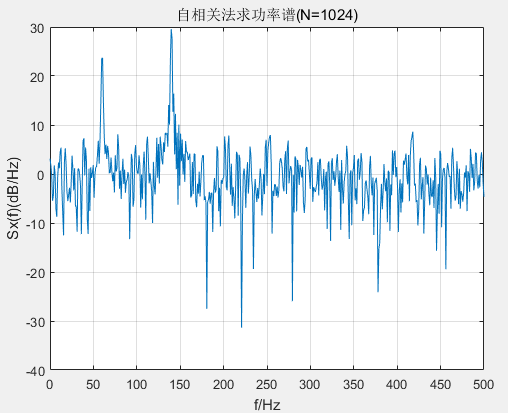
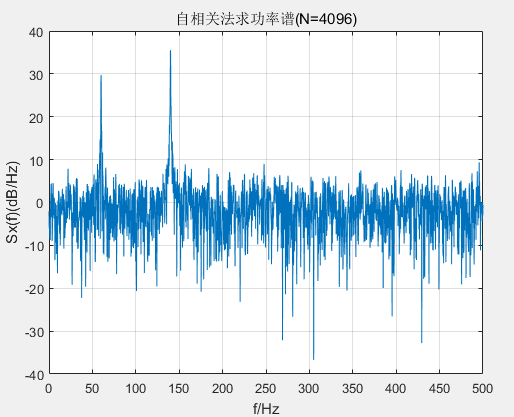
可以看到随着N点数的增加，功率谱分辨率得到了提升，但是起伏加剧，也就是分辨率和方差是一对矛盾。

3、改进的功率谱估计——分段平均法和加窗平均法

（1）分段平均（分段加矩形窗）

clear all
clear

N=4096;%采样点数
fs=1000;%采样频率，满足采样定理
t=(0:N-1)/fs;%时间，平分了1024份。（0~1.24s）
fai=random('unif',0,1,1,2)*2*pi;%两个相位
A=[1,2];%两个振幅
f=[30,70];%两个频率，可以计算出信号周期
x=A(1)*cos(2*pi*f(1)*t+fai(1))+A(2)*cos(2*pi*f(2)*t+fai(2))+randn(size(t));%该信号
Nseg=1024;
win=rectwin(1024)';%加矩形窗
Sx1=abs(fft(win.*x(1:1024)).^2/norm(win)^2);%2范数，平方求和开根号还是 1024
Sx2=abs(fft(win.*x(1025:2048)).^2/norm(win)^2);%2范数，平方求和开根号还是 1024
Sx3=abs(fft(win.*x(2049:3072)).^2/norm(win)^2);%2范数，平方求和开根号还是 1024
Sx4=abs(fft(win.*x(3073:4096)).^2/norm(win)^2);%2范数，平方求和开根号还是 1024
f=(0:Nseg/2-1)*fs/Nseg;%频率范围（一半）(0~500Hz)
Sx=[Sx1;Sx2;Sx3;Sx4];
for ii=1:4
    subplot(211),plot(f,10*log10(Sx(ii,1:Nseg/2)));%4段估计
    hold on
end
legend('Sx1','Sx2','Sx3','Sx4')
xlabel('f/Hz');ylabel('Sx(f)(dB/Hz)');
title('分段估计功率谱')
grid on 

ESx=(10*log10(Sx1)+10*log10(Sx2)+10*log10(Sx3)+10*log10(Sx4))/4;%求平均
subplot(212),plot(f,ESx(1:Nseg/2));%平均值
xlabel('f/Hz');ylabel('Sx(f)(dB/Hz)');
title('分段平均估计功率谱')
grid on 

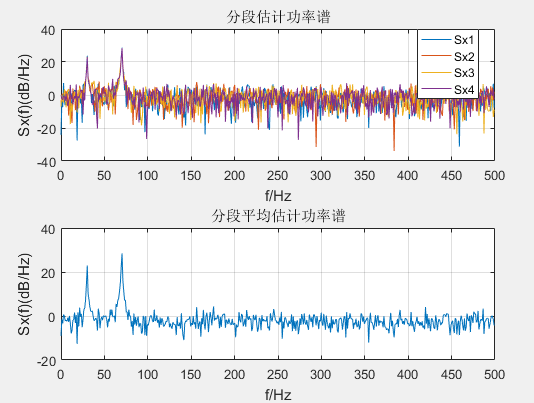
（2）加汉宁窗

将上面程序矩形窗改为汉宁窗

win=hanning(1024)';%汉宁窗　　

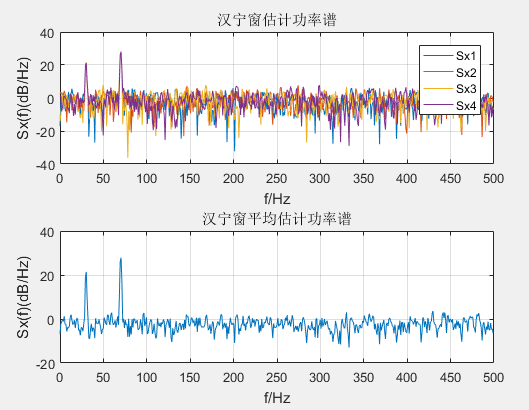
可以看出，分辨率和方差性能都得到提升。

4、Welch方法

clear all
clear

N=4096;%采样点数
fs=1000;%采样频率，满足采样定理
t=(0:N-1)/fs;%时间，平分了1024份。（0~1.24s）
fai=random('unif',0,1,1,2)*2*pi;%两个相位
A=[1,2];%两个振幅
f=[30,70];%两个频率，可以计算出信号周期
x=A(1)*cos(2*pi*f(1)*t+fai(1))+A(2)*cos(2*pi*f(2)*t+fai(2))+randn(size(t));%含噪信号

Nseg=1024;%分段长度
win=hanning(1024)';%1024点汉宁窗
noverlap=Nseg/2;%重叠点数
f=(0:Nseg/2)*fs/Nseg;%频率坐标
Sx=pwelch(x,win,256,Nseg,fs,'onesided')*fs/2;%Welch法单边功率谱估计

plot(f,10*log10(Sx));%平均值
xlabel('f/Hz');ylabel('Sx(f)(dB/Hz)');
title('Welch法估计功率谱')
grid on 

5、歌曲实例

（1）

clear all
clear
[song,fs]=audioread('李健 - 贝加尔湖畔 (自白版).mp3',[1290001,1910000]); % loads 
N=length(song(:,1));%采样点数
fs=16000;%采样频率，满足采样定理
for ii=1:2
    x=song(:,ii);%该信号
    Sx(:,ii)=(abs(fft(x).^2/N));
end
f=(0:N/2-1)*fs/N;%频率
subplot(211),plot(1:N,song(:,1),1:N,song(:,2))
xlabel('n');ylabel('f(x)');
title('原始双声道数据')
legend('1声道','2声道')
grid on 
subplot(212),plot(f,10*log10(Sx(1:N/2,1)),f,10*log10(Sx(1:N/2,2)));
xlabel('f/Hz');ylabel('Px(f)(dB/Hz)');
title('两个声道声道频谱图')
legend('1声道','2声道')
grid on

figure
subplot(221),plot(f,10*log10(Sx(1:N/2,1)));
xlabel('f/Hz');ylabel('Px(f)(dB/Hz)');
title('1声道声道频谱图')
grid on
%Yule-Walker谱估计对象
Hs=spectrum.yulear(16);
subplot(222)
psd(Hs,song(:,1),'fs',16000,'nfft',1024)

subplot(223),plot(f,10*log10(Sx(1:N/2,2)));
xlabel('f/Hz');ylabel('Px(f)(dB/Hz)');
title('2声道声道频谱图')
grid on
%Yule-Walker谱估计对象
Hs=spectrum.yulear(16);
subplot(224)
psd(Hs,song(:,2),'fs',16000,'nfft',8096)

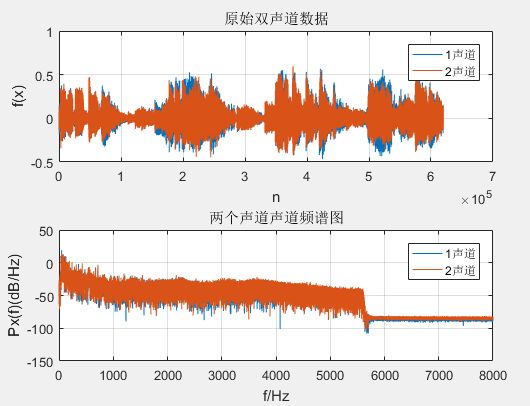
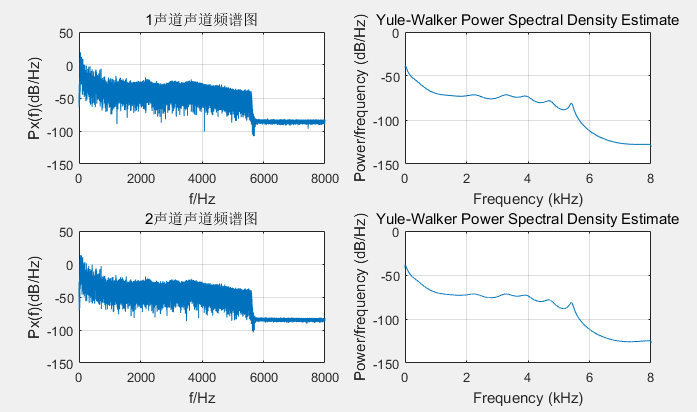
两个声道的时域和频域图。可以看出两个声道声音几乎一致。

（2）　　

clear all
clear
clear all
clear
[song1,fs]=audioread('李健 - 贝加尔湖畔 (自白版).mp3',[1290001,1910000]); % loads 
% sound(song,fs)
[song2,fs]=audioread('李健 - 贝加尔湖畔 (自白版).mp3',[1910001,2530000]); % loads 
% sound(song,fs)
song(:,1)=song1(:,1);
song(:,2)=song2(:,1);
sound(song,fs)

左右耳机出来不一样的音乐。　　

6、典型随机过程

（1）

白噪声：均值为0

平稳白噪声：均值为0，功率谱为定值（所有频率都有，并且值一样），自相关函数只在0处有一个冲击

%平稳高斯白噪声
clear all
clear
x=randn(5000,1);
N=length(x);
fs=200;
subplot(221)
plot(x);
xlabel('n'),ylabel('x(n)');
title('平稳高斯白噪声');
grid on

subplot(222)
y=histogram(x,20)
xlabel('x'),ylabel('n/个');
grid on

Rx1=xcorr(x,'biased');%自相关函数
m=(-N+1):(N-1);%
subplot(223)
plot(m,Rx1);
xlabel('m');ylabel('Rx1');
axis([-N+1 N-1 -1 1.5]);
grid on;
title('平稳高斯白噪声自相关函数');

Sx=(abs(fft(x)).^2)/N;%功率谱密度公式
f=(0:N/2-1)*fs/N;%频率范围（一半）
subplot(224),plot(f,Sx(1:N/2));
xlabel('f/Hz');ylabel('Sx(f)/Hz');
grid on
 

（2） 　

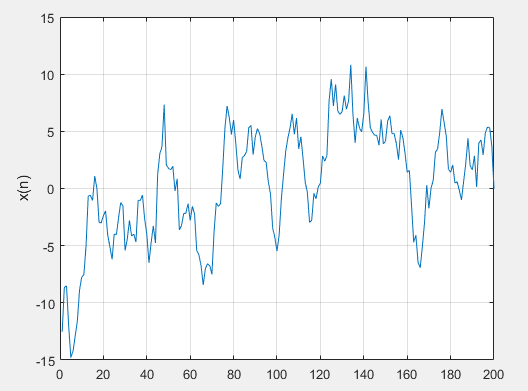
clc
clear all
a=0.95;
sigma=2;
N=200;
u=randn(N,1);
x(1)=sigma*u(1)/sqrt(1-a^2);
for ii=2:N
    x(ii)=a*x(ii-1)+sigma*u(ii);
end
plot(x);
axis([0,200,-15,15])
xlabel('n')
ylabel('x(n)')
grid on
figure
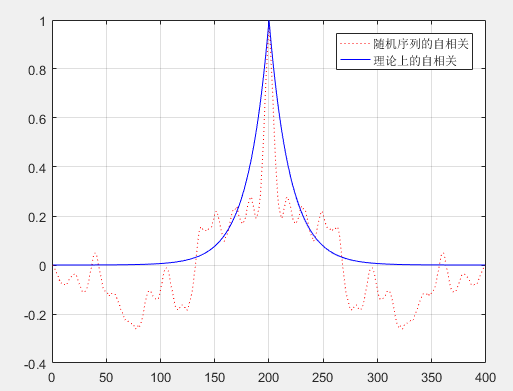
R=xcorr(x,'coeff');%归一化
plot(R,':r');
hold on 
M=1:399;
Rx=sigma^2/(1-a^2)*a.^abs(M-200);
Rx=Rx/((sigma^2)/(1-a^2));%归一化
plot(Rx,'-B')
grid on
legend('随机序列的自相关','理论上的自相关')