参考教程 python 手动搭建ANN，并进行具体实现

用 Python 手动进行 ANN 的搭建（简单的BP型网络），可加深对其深入的理解，同时熟练coding，具有xxx、yyy之功效。

网上手动建NN的帖子有不少，不过多数没有实现过程，这里把这一部分补上，方便大家参考使用。

前半步主要是参考如下的帖子，建立 ANN：

• https://towardsdatascience.com/how-to-build-your-own-neural-network-from-scratch-in-python-68998a08e4f6

  但这个帖子有个问题，就是建立了ANN 却并没有实现过程，同时其中前后传播方法的‘feedforward’和 ‘backprop’ 中的sigmoid函数及其导数也没有具体的函数定义。

 

• 因此，进一步参考如下的网页：

• http://python3.codes/neural-network-python-part-1-sigmoid-function-gradient-descent-backpropagation/
• http://python.jobbole.com/82758/

  另外下面的这个也不错，只是有点太细碎了，大线条看着有点乱：

• http://www.bogotobogo.com/python/python_Neural_Networks_Backpropagation_for_XOR_using_one_hidden_layer.php

以下具体步骤：

1. 建立 ANN：

 有些说明在注释中写了。

class NeuralNetwork:
    
    # 通过初始化的方式实现 输入‘x’及输出‘y’、以及网络权重（定义了二层4节点的网络结构） 的基本结构：
    def __init__(self, x, y):
        self.input = x
        self.weights1 = np.random.rand(self.input.shape[1],4) 
        # 这样的结构，意味着weights1的行数是输入变量x的列数，那么相乘时可能是与常规的 W·X 的方式相反，即 X·W
        # 因此，X的每一行，代表着一次x输入，对应着每一个输出y
        
        # 同上的，这样的结构形式定义，代表的表达式或应是：[(X·W1+b1)·W2]+b2
        ## 而在经过上述W1与W2的相乘后，每一行的x对应着一个y_i的值
        self.weights2 = np.random.rand(4,1)
        
        # 对应着y作为输出，定义self.output 的结构
        self.y = y
        self.output = np.zeros(y.shape)

    
    def feedforward(self): #定义前传方法：
        # 注意忽略了每层的偏差 b_i
        # 且转换函数使用 sigmoid()
        # 因没有相应的函数定义，将其中的 sigmoid() 函数进行展开
        # sigmoid(m)=1/(1 + np.exp(-m))
       
        npDotW1_Inpt = np.dot(self.input, self.weights1)
        self.layer1 = 1/(1+np.exp(-1*npDotW1_Inpt))
        
        npDotL1_W2 = np.dot(self.layer1, self.weights2)
        self.output = 1/(1+np.exp(-1*npDotL1_W2))
        
    def backprop(self): # 定义后传方法：
        # application of the chain rule to find derivative of the loss function with respect to weights2 and weights1
        # 以上是原文注解，即在向后传播 backprop 时，使用链式法则获得相应权重值的损失函数
        # 因没有相应的函数定义，将原贴中的 sigmoid_derivative() 函数进行展开
        # sigmoid_derivative(m)=m * (1 - m)

        ## 此处采用的是 s_deriv(x) = x*(1-x) 的方式，如采用 exp(-x)/(1+exp(-x))^2) 的解析式也可以，本质相同：
        d_weights2 = np.dot(self.layer1.T, (2*(self.y - self.output) * (self.output*(1-self.output))))
        d_weights1 = np.dot(self.input.T,  (np.dot(2*(self.y - self.output) * (self.output*(1-self.output)), self.weights2.T) * (self.layer1*(1-self.layer1))))
    
        # update the weights with the derivative (slope) of the loss function
        # 通过上面的求导斜率，对W1和W2进行更新：
        self.weights1 += d_weights1
        self.weights2 += d_weights2            

2. 实现过程：

此步原文没有写，估计作者觉得太简单了，貂尾续根草吧。

但这里的输入和输出是按原文给的，便于对比实现结果是否一致。

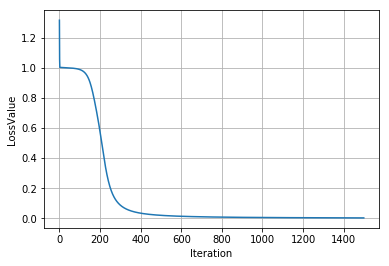
# 建立输入和输出变量：
x_input = np.array([[0,0,1],[0,1,1],[1,0,1],[1,1,1]])
y_obj = np.array([[0,1,1,0]]).T

# 实例化 ANN：
nn = NeuralNetwork(x_input, y_obj)

# 进行计算，迭代次数为1500次：
m = 1500
loss = np.zeros(m)

for i in range(m):
    nn.feedforward() # 前传计算结果
    nn.backprop() # 后传更新权重

    loss[i] = np.sum((nn.output-y_obj)**2) # 记录每次的结果偏差

# 绘制结果图形：
plt.plot(loss)
plt.xlabel('Iteration')
plt.ylabel('LossValue')
plt.grid(True)

结果如图：

Enjoy it  :)