浅析点分治实现过程及时间复杂度

概要

带权无根树上简单路径统计问题的算法
将树上问题转化为子问题求解，每次统计字节点贡献求和即可

引入

Luogu P4178 Tree
题目大意，给一棵树一个(k)，求距离小于等于(k)的点对数量

暴力

(LCA)板子直接(T30)没啥说的

正解——点分治

点分治

• 从一个点开始(dfs)，求出到这个点距离
• 枚举距离(l)和(r)，对于(a[l]+a[r]<=k)统计答案

根的选取（重心的定义）

对于一棵无根树，找到一个点，使得满足如果以它为根，它的最大子树大小尽量小，这个点称为重心。

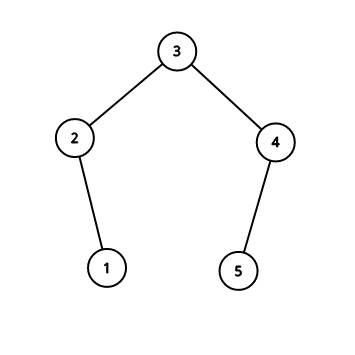
比如这条链状结构，如果选取1为根节点，递归时间复杂度飙升至(O(N^2))，如果选取重心3作为根节点那么时间复杂度维持在(O(nlog_n))

重心的性质

• 删去该点后，最大子树的大小最小
• 以树的重心为根的每棵子树大小不超过(frac n 2)（证明……yy一下就好了吧，太简单了不写了）
• 由第二条推导出，递归整棵树的时间复杂度是(O(log;n))
• 一个子节点统计一次答案复杂度为(O(n;log;n))

算法流程

• (dfs)查找树的重心
• (dfs)求出每个点到重心的距离，并且将距离存进一个数组
• 枚举距离数组中满足(a[i]+a[j]<=k)的情况统计答案
• 递归至下一个子节点重复上述步骤直至整棵树搜索完毕

特殊处理

在处理树上两个点的时候，两点的位置关系一共有三种

• 两点在同一棵子树上
• 两点在不同子树上
• 一个点在子树内，一个是重心
  显然，对于2和3两种情况没啥问题
  但是对于第一种情况
  
  显然，2和4的距离在实现过程中会有两种处理方式，一种是通过简单路径，一种是通过1计算的路径
  第二种是不合法的，所以统计答案时要减去

Code

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;

inline int read(){
	int x = 0, w = 1;
	char ch = getchar();
	for(; ch > '9' || ch < '0'; ch = getchar()) if(ch == '-') w = -1;
	for(; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';
	return x * w;
}

const int ss = 1000010;

struct node{
	int to, nxt, w;
}edge[ss << 1];

int head[ss << 1], tot;
inline void add(int u, int v, int w){
	edge[++tot].to = v;
	edge[tot].nxt = head[u];
	edge[tot].w = w;
	head[u] = tot;
}

int size[ss], sz, maxx[ss], root;
bool vis[ss];
inline void getroot(register int u,register  int f){
	size[u] = 1;
	maxx[u] = 0;
	for(register int i = head[u]; i; i = edge[i].nxt){
		register int v = edge[i].to;
		if(v == f || vis[v]) continue;
		getroot(v, u);
		size[u] += size[v];
		maxx[u] = max(maxx[u], size[v]);
	}
	maxx[u] = max(maxx[u], sz - size[u]);
	maxx[u] = maxx[u];
	if(maxx[u] < maxx[root]) root = u;
}

int a[ss], cnt;
inline void getdis(int u, int f, int d){
	a[++cnt] = d;
	for(int i = head[u]; i; i = edge[i].nxt){
		int v = edge[i].to;
		if(v == f || vis[v]) continue;
		getdis(v, u, d + edge[i].w);
	}
}

int n, k;
inline int calc(int u, int d){
	int sum = 0;
	cnt = 0;
	getdis(u, 0, d);
	sort(a + 1, a + 1 + cnt);
	int r = cnt;
	for(int l = 1; l <= cnt; l++){
		while(r && a[l] + a[r] > k) r--;
		if(l > r) break;
		sum += r - l + 1;
	}
	return sum;
}

int ans;
inline void divide(int u){
	ans += calc(u, 0);
	vis[u] = 1;
	for(int i = head[u]; i; i = edge[i].nxt){
		int v = edge[i].to;
		if(vis[v]) continue;
		ans -= calc(v, edge[i].w);
		root = 0;
		sz = size[v];
		getroot(v, u);
		divide(v);
	}
}

signed main(){
	n = read();
	for(int i = 1; i <= n - 1; i++){
		int u = read(), v = read(), w = read();
		add(u, v, w);
		add(v, u, w);
	}
	k = read();
	maxx[0] = 0x7fffffff;
	getroot(1, 0);
	divide(root);
	cout << ans - n << endl;
	return 0;
}

小结

掌握分治思想&容斥操作