Problem
1492 C. Maximum width
给两个字符串 s 和 t ,s的长度为n, t的长度为m, 且 t 为 s 的子串
也就是可以取p1,p2,p3....pm,使得t[pi] == s[i] (p1 < p2 < ...< pm)
求max(pi+1 - pi) 最大为多少
2 <= m <= n <= 2e5
1499 D. The Number of Pairs
T组输入,每组输入三个数c,d,x
求满足c * lcm(a,b) - d * gcd(a,b) = x的a,b有多少对
例:c = 1,d = 1, x = 3 , a,b可取(1,4),(4,1),(3,6),(6,3)
1 <= t <= 1e4 , 1<= c,d,x <= 1e7
1499 E. Chaotic Merge
有两个字符串x,y
字符串z一开始是空串,每次操作,可以从x串或y串左端剪切一个字母,粘贴到z串的右端,一直重复操作直到x串和y串都变为空串为止
我们称一个字符串是chaotic的,当且仅当这个字符串所有相邻的两个字符不同
输入两个串 s 和 t
f (L1,R1,L2,R2) 表示x串等于s串的[L1,R1]部分,y串等于 t串的[L2,R2]部分时,有多少种不同的操作序列,使得 z串是chaotic的
求Σf(L1,R1,L2,R2) (1<=L1<=R1<=len(s) ,1<=L2<=R2<=len(t))
答案对998244353取膜
1 <= len(s),len(t) <= 1000
Solution
1492 C. Maximum width
我们想要让某两个相邻的pi相差最大,来更新ans
那么就是考虑对于某个数x, px+1 - px 最大是多少
那么就要使px越小越好,px+1越大越好
求pi的最小值,就是把s串从左往右扫一遍,一旦匹配的上就去匹配
同理求pi的最大值,就是把s串从右往左扫一遍
code:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int MAXN = 2e5+7;
int pos1[MAXN],pos2[MAXN];
int main()
{
int n,m;
string s,t;
cin>>n>>m;
cin>>s>>t;
s = " " + s;
t = " " + t;
int pos = 1;
for(int i = 1;i <= n;i++){
if(s[i] == t[pos]){
pos1[pos] = i;
pos++;
if(pos > m) break;
}
}
pos = m;
for(int i = n;i;i--){
if(s[i] == t[pos]){
pos2[pos] = i;
pos--;
if(pos<=0) break;
}
}
int ans = pos2[2] - pos1[1];
for(int i = 3;i <= m;i++){
ans = max(ans,pos2[i] - pos1[i-1]);
}
cout<<ans<<endl;
return 0;
}
1499 D. The Number of Pairs
首先得考虑gcd和lcm能取什么
可以发现,lcm % gcd == 0,gcd % gcd == 0, (c * lcm - d * gcd) % gcd = 0 = x % gcd
那么gcd只能是x的因数了
于是我们可以枚举gcd,再通过c * lcm - d * gcd = x这个方程算出lcm,然后检查lcm是否为gcd的倍数
当gcd(a,b)和lcm(a,b)都确定下来后,怎么算a,b有多少对?
这个可以从素数分解考虑,可以自己分析
可以考虑只有一个质因数的情况,然后多质因数的情况就是乘法原理了
但是这样还会TLE,怎么办?
可以用记忆化搜索的方法,也可以用离线算法
code:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int MAXN = 2e7 + 7;
int f[MAXN], zx[MAXN], zs[MAXN], tot = 0;
void pre(int n) {
for (int i = 2; i <= n; i++) {
if (!zx[i]) zs[++tot] = zx[i] = i;
for (int j = 1; j <= tot; j++) {
if (n / zs[j] < i) break;
zx[i * zs[j]] = zs[j];
if (zx[i] == zs[j]) break;
}
}
}
int ins(int x) {//lcm / gcd == x的时候,(a,b)的对数有多少对
if (f[x]) return f[x];//记忆化
int t = x;
int cnt = 0;
while (t != 1) {
int xx = zx[t];
cnt++;
while (t % xx == 0) t /= xx;
}
return f[x] = 1 << cnt;
}
int main()
{
int T;
pre(MAXN);
long long a, b, c, d, x;
cin >> T;
while (T--) {
cin >> c >> d >> x;
long long gd, lc;
int ans = 0;
for (long long i = 1; i * i <= x; i++) {
if (x % i == 0) {
gd = i;//gcd = i
lc = x + d * gd;//lcm
if (lc % c == 0) {
lc /= c;
if (lc % gd == 0) {
ans += ins(lc / gd);
}
}
if (x / gd != gd) {//gcd = x / i
gd = x / gd;
lc = x + d * gd;
if (lc % c == 0) {
lc /= c;
if (lc % gd == 0) {
ans += ins(lc / gd);
}
}
}
}
}
cout << ans << endl;
}
return 0;
}
1499 E. Chaotic Merge
首先来思考这两个串都取最大区间的情况,即完整的s串和完整的t串,有多少种操作序列
可以想到这是一个字符串上的dp题
最经典的字符串dp题就是求两个串的最长公共子串了,这个经典的问题可以用dp[ i ][ j ]表示 s取[1, i ],t 取[1, j ] 时的最长公共子串长度
那么这题也类似,先考虑用dp[ i ][ j ]表示s串取[1, i ], t串取[1, j ]时的操作序列数
思考转移过程的时候发现这样还是不够的,我们要关注z串最后一个字母是什么,这便要看最后一个操作是取x串的还是取y串的了
于是我们用dp[ i ][ j ][ 0 ]表示s串取[1, i ],t串取[1, j ],且最后一个操作是取x串的操作序列个数, dp[ i ][ j ][ 1 ]则表示的是最后一个操作是取y串的
在草稿纸上可以推出4个转移方程
转移方程的代码如下:
dp[1][0][0] = dp[0][1][1] = 1;
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
if(a[i] != a[i - 1]){
dp[i][j][0] += dp[i - 1][j][0];
}
if(a[i] != b[j]){
dp[i][j][0] += dp[i - 1][j][1];
}
if(b[j] != b[j - 1]){
dp[i][j][1] += dp[i][j - 1][1];
}
if(b[j] != a[i]){
dp[i][j][1] += dp[i][j - 1][0];
}
}
}
这个子问题就解决了,子问题的难度大概在1500分左右吧
我们发现解决这个子问题的同时,我们不仅求出了s串和t串取最大区间时的答案,还求出了s串取[1, i ]时,t串取[1, j]时的答案,也就是求出了len(s)*len(t)个答案
如果我们还要再求所有s串取[1, i ]时,t 串取[2, j ]时的答案,那就要再跑一遍dp转移方程,但是这次跑的时候,要初始化一遍,起点也不一样了,但是哪些点转移到哪些点还是不变的!
所以我们每次重新跑一遍dp的时候,就是起点变了而已
举个简单的例子,假设有dp[ i ] = dp[ i - 1] + dp[i - 2] + i,有一次从dp[1] = dp[2] = 0开始跑,另一次是从dp[4] = dp[5] = 0开始跑,这就是只有起点变了
分析仅仅是起点变了,贡献有哪些变化
我们可以把dp[ i ][ j ][ k ]看成是一个点,把有转移关系的点之间连一条有向边
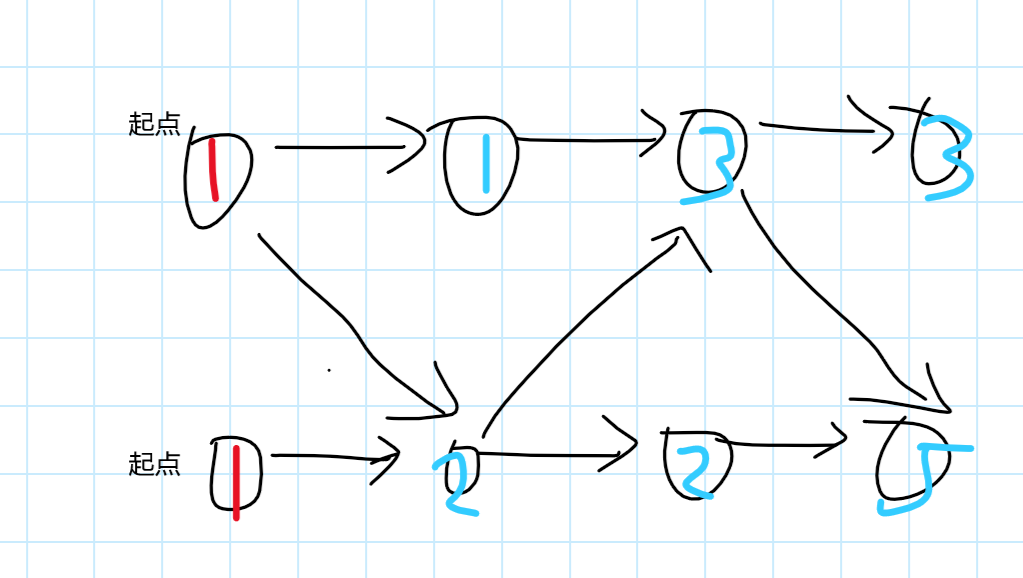
如图,之前讲的子问题,就是从dp[1][0][0] = 1和dp[0][1][1] = 1这两个起点开始
如果把下面的起点换个位置
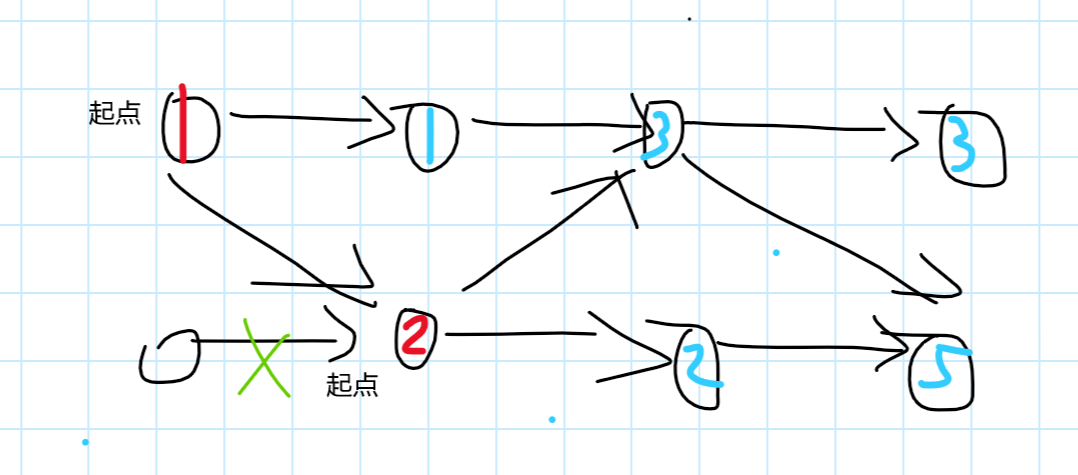
那么就是这种情况了
两个起点分别的贡献是:
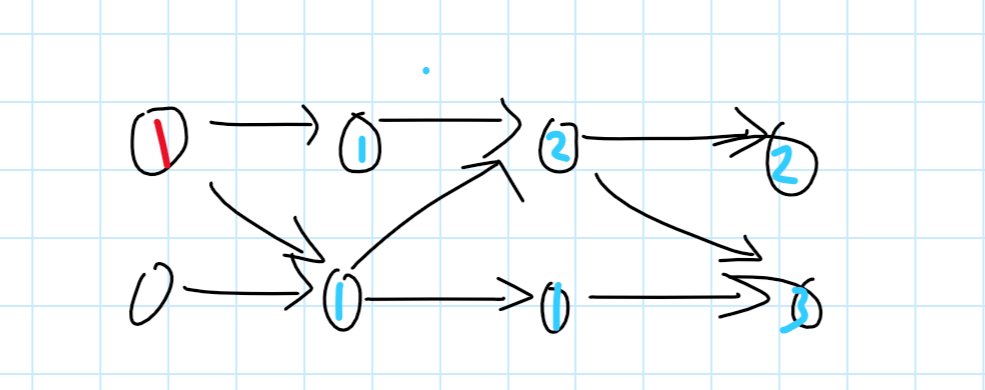
和
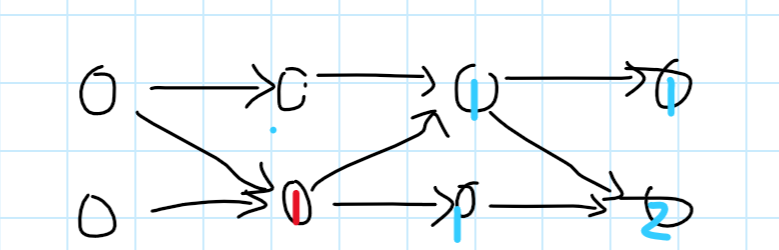
显然这两个起点是独立的
现在我们要做的是,如何快速求出,当一个点为起点时,且这个起点上的值为1,能产生多少贡献
这显然又是一个dp
我是用siz[i][j][k]表示这个点为起点且点上的值为1时,产生的贡献为多少
关于siz[i][j][k]的递推代码 (注意初始化和取膜) :
for(int i = 0;i<=n;i++)
for(int j = 0;j<=m;j++)
siz[i][j][0] = siz[i][j][1] = 1;
for(int i = n;i>=0 ;i--){
for(int j = m;j>=0 ;j--){
if(i && a[i] != a[i-1]) {
//dp[i][j][0] += dp[i-1][j][0];
//dp[i][j][0]表式a串取1到i,b串取1到j,要使merge串的最后一位是a串的最后一位的构造方案数
siz[i-1][j][0] += siz[i][j][0];
siz[i-1][j][0] %= MOD;
}
if(i && a[i] != b[j]){
//dp[i][j][0] += dp[i-1][j][1];
siz[i-1][j][1] += siz[i][j][0];
siz[i-1][j][1] %= MOD;
}
if(j && b[j] != b[j-1]){
//dp[i][j][1] += dp[i][j-1][1];
siz[i][j-1][1] += siz[i][j][1];
siz[i][j-1][1] %= MOD;
}
if(j && b[j] != a[i]){
//dp[i][j][1] += dp[i][j-1][0];
siz[i][j-1][0] += siz[i][j][1];
siz[i][j-1][0] %= MOD;
}
}
}
还要注意x串和y串是不能为空的,所以还要减去x串或y串为空的情况
比如在最开始的子问题里,要减去所有dp[i][0][0],减去所有dp[0][j][1]
这个也可以用dp算出某个点为起点时,能有多少种方案
我是用sza[i]和szb[i]表示
for(int i = 1;i<=n;i++) sza[i] = 1;
for(int i = n;i;i--){
if(a[i] != a[i-1]) sza[i-1] += sza[i];
}
for(int i = 1;i<=m;i++) szb[i] = 1;
for(int i = m;i;i--){
if(b[i] != b[i-1]) szb[i-1] += szb[i];
}
总的代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;
const int MAXN = 1e3+7;
const long long MOD = 998244353;
int n,m;
long long dp[MAXN][MAXN][2];
long long siz[MAXN][MAXN][2];
int sza[MAXN],szb[MAXN];
int main()
{
string a,b;
cin >> a >> b;
n = a.length();m = b.length();
a = " " + a;
b = " " + b;
int u,v;
long long ans = 0;
for(int i = 0;i<=n;i++)
for(int j = 0;j<=m;j++)
siz[i][j][0] = siz[i][j][1] = 1;
for(int i = n;i>=0 ;i--){
for(int j = m;j>=0 ;j--){
if(i && a[i] != a[i-1]) {
//dp[i][j][0] += dp[i-1][j][0];
//dp[i][j][0]表式a串取1到i,b串取1到j,要使merge串的最后一位是a串的最后一位的构造方案数
siz[i-1][j][0] += siz[i][j][0];
siz[i-1][j][0] %= MOD;
}
if(i && a[i] != b[j]){
//dp[i][j][0] += dp[i-1][j][1];
siz[i-1][j][1] += siz[i][j][0];
siz[i-1][j][1] %= MOD;
}
if(j && b[j] != b[j-1]){
//dp[i][j][1] += dp[i][j-1][1];
siz[i][j-1][1] += siz[i][j][1];
siz[i][j-1][1] %= MOD;
}
if(j && b[j] != a[i]){
//dp[i][j][1] += dp[i][j-1][0];
siz[i][j-1][0] += siz[i][j][1];
siz[i][j-1][0] %= MOD;
}
}
}
for(int i = 1;i<=n;i++) sza[i] = 1;
for(int i = n;i;i--){
if(a[i] != a[i-1]) sza[i-1] += sza[i];
}
for(int i = 1;i<=m;i++) szb[i] = 1;
for(int i = m;i;i--){
if(b[i] != b[i-1]) szb[i-1] += szb[i];
}
for(int l = 1;l <= n;l++){//枚举左右起点
for(int r = 1;r <= m;r++){
ans += siz[l][r-1][0] + siz[l-1][r][1] - sza[l] - szb[r];
//起点是dp[l][r-1][0] = 1 和 dp[l-1][r][1] = 1
ans = (ans % MOD + MOD) % MOD;
}
}
cout<<ans<<"
";
return 0;
}
总结一下,这题首先是一个字符串的dp问题,然后题目还要求计算取尽所有起点的情况的答案之和
由于只有起点变化,有向边没有变,于是让人思考起点或起点上的值改变时,其对贡献的变化是怎样的