常数时间国密算法

常数时间国密算法（三）：SM2的素域求逆技术 https://mp.weixin.qq.com/s/4dOgGKJ7bwTxsHr-xekz0Q

常数时间国密算法（三）：SM2的素域求逆技术

原创 高能链 哔哩哔哩技术 2022-08-23 12:00 发表于上海

收录于合集

#B站54个

#加密算法3个

本期作者

郭伟基

哔哩哔哩技术专家

负责B站高能链密码学、区块链相关技术研究与开发，特别是密码学技术的安全、高效实现，以及应用密码学技术实现链上隐私保护和业务赋能。

现在我们来看SM2常数时间实现的另一个技术点，即素域求逆。在这篇文章，我们先介绍SM2的签名验签算法，指出实现中的安全隐患，然后介绍相关的数学知识，最后讲解如何安全地实现签名验签算法。

01 SM2签名算法简单介绍

素域求逆是SM2签名算法所要求的。使用规范文本GMT 0003.2-2012的符号约定：

• e    为原始待签名信息、椭圆曲线公共参数、签名者信息的综合摘要，为一个256位整数；

• k    为使用安全的随机数生成器所生成的随机数，取值范围[1, n-1]，其中n为椭圆曲线的参数，并且是一个素数；

• d_A  为签名用户的私钥，为一个256位的整数。

则SM2所规定的签名算法要求计算：

• (x₁, y₁) = [k]G

• r = (e + x₁) mod n，其中mod表示同余

• 判断 r 是否为0或者r + k = n。如是（概率极小），需要重新生成k、重复以上计算步骤，否则进入下一步；

• s = (k - r*d_A) / (1 + d_A) mod n

• 如果s非零（大概率），则返回（r, s）作为签名结果。否则需要重新生成k、重复以上计算步骤。

在以上计算s的公式中，需要除以（1 + d_A），或者说需要乘以（1 + d_A）的乘法逆元。这就是求逆计算的来源。

细心的读者可能会问，如果我们一直处理的都是各种大整数，那么这里的除法要怎么做，除不尽又怎么办呢？这就不得不说，这里其实有一套特殊的计算法则，不会除不尽了。

02 素域与素域求逆

一般而言，两个大整数相除，很可能会发生除不尽、产生小数甚至分数（无限循环小数）的情况。我们知道，浮点数在计算机中可能无法精确表示，针对浮点数的计算，常常会产生各种误差。这种误差在密码学中极为致命，一般不允许出现。密码学中，需要一套计算法则来避免这种情况。这就是有限域，其中基于某个素数p产生的有限域称为素域，一般记为F_p。

素域F_p的计算法则其实非常简单：它只需要在通常的加法和乘法规则上加一个除以该p取余数的规定。而所谓的“有限”（域），也很直观：素域F_p的元素个数有限，不多不少正好p个。在这些元素中，0为加法的单位元，也就是任何元素与之相加，所得仍是该数；1为乘法的单位元。我们可以把减法定义为加法的逆运算，除法定义为乘法的逆运算，但一般不使用除法这个术语，而称为乘法求逆：某个元素a（非零）的乘法逆元a^-1定义为某个b，使得：

a * b ≡ 1 mod p

在数学上，这样的逆元总是存在的（前提是a ≠ 0）。这也就回答了之前的问题：除不尽怎么办。因此，我们总是能够完成以上计算s值的步骤（规范要求d_A ≠ n - 1，以保证分母不为零）。

现在，我们只是说了非零元素的逆元总是存在，那么要怎么样才能把逆元计算出来呢？一般而言可以使用扩展欧几里得算法，一般在大整数相关的函数库或类库中均有实现；另外就是费马小定理方法。下面分别加以介绍。

03 辗转相除法与扩展欧几里得算法

小时候学习过奥数，或者正在辅导小孩学奥数的读者可能对辗转相除法不陌生，这是求两个数的最大公约数（gcd）的一种方法：设有a, b两数，我们反复以其中较小者去除其中较大者，然后取余数以替代除数，原除数作为新的被除数，直到余数为零，则最后一个除数即为 a 和 b 两者的最大公约数。此方法可以制作成表格形式，更为直观，譬如计算gcd(32, 12)：

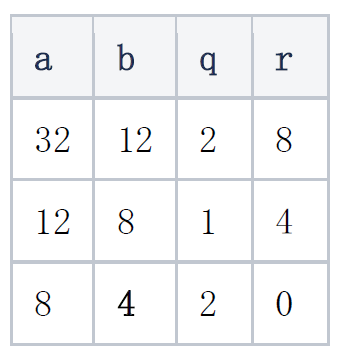
以上表格，最后一行我们得到余数为0，那么该行的除数也就是所求的最大公约数了，因此gcd(32, 12) = 4。这就是辗转相除法，又称欧几里得算法。而所谓的扩展欧几里得算法，就是将上表再加以扩展，添加若干列，以便求得u, v使得u*a + v*b = gcd(a, b)。具体讲解该方法之前，我们需要解释一下，为何使用扩展欧几里得算法就能求得素域元素的乘法逆元。假设有p, b两个数，其中 p 为素数，b < p，那么这两个数互素，其最大公约数为1；如果使用扩展欧几里得算法能够得到 u 和 v 使得 u*p + v*b = gcd(p, b) = 1，那么实际上，v就是 b 在素域 F_p 上的乘法逆元：v*b ≡ 1 mod p。注意，这里我们已经只关心 v 的取值而不用管 u 了。

仍以前述数字为例，在表格右方添加三列：v₁, v₂, v₃，分别逐行作如下计算（完整的扩展欧几里得算法需要添加六列，但我们这里不关心 u ）：

• 其初始值设定为：v₁ := 0, v₂ := 1, v₃ := v₁ - q*v₂ （同一行）

• 每一新行：v₁ = 上一行的v₂，v₂ = 上一行的v₃，v₃ = v₁ - q*v₂ （同一行；同上）

• 在 r = 0的那行，令 v = v₂，而v₃可以不用计算

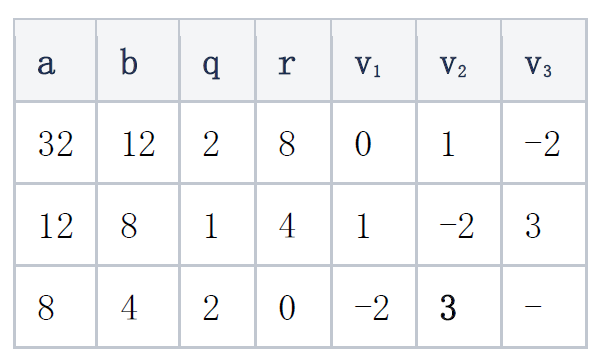
因为我们没有计算 u ，所以无法直接验证v = 3是否我们需要的结果。但是在素域求逆的情况下，这就够了。下面以p = 19, b = 10 为例，计算10在素域F₁₉上的乘法逆元：

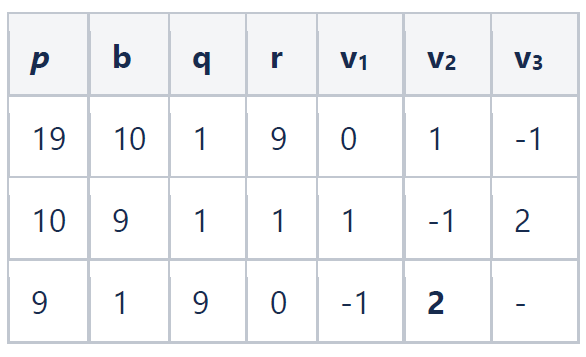
得到 v = 2。验证：10 * 2 = 20 ≡ 1 mod 19

在SM2的签名算法计算过程中，素数 p 是既定的（椭圆曲线的参数 n ），需要保护的是被求乘法逆元的那个数（1 + d_A）。然而从上述计算过程我们可以看到，所用表格的行数可能会取决于被计算的数。换句话说，以上形式的扩展欧几里得算法实现可能具有非常数时间特性，可能导致所计算元素的值被破解。以下再给出一个计算p = 19, b = 6 的实例，其计算表格比上一个实例少一行：

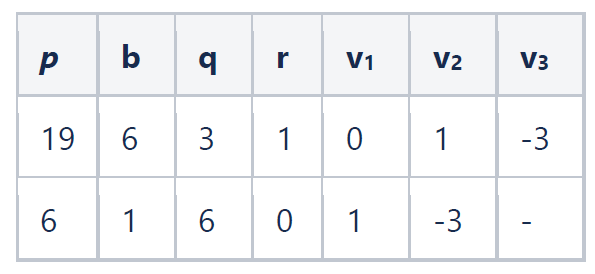
得到 v = -3，在F₁₉里面，也就是16。验证：6 * 16 = 96 = 1 + 5*19 ≡ 1 mod 19

因此，虽然扩展欧几里得算法具有快速、现成易得的好处，它不应该被用于在SM2的签名算法中计算(1 + d_A)^-1，否则可能导致私钥的破解。在上一篇文章的最后我们提到，有时候为了避免基于敏感值去作代码分支，除了应用Select方法，我们还可以将算法整体更换掉；现在，我们要使用一个新的算法来进行素域求逆计算。

04 费马小定理方法

基于费马小定理可以达到常数时间计算素域乘法逆元的目的。我们先来看费马小定理是如何表述的：

如果p为素数，则对任意整数 a 均有：a^p ≡ a mod p

附加 a 不是 p 的倍数（即a, p 互素）的条件，并稍稍变换一下形式，就是：

a^p-1 ≡ 1 mod p

a^p-2 ≡ a^-1 mod p

也就是说，要计算 a 在F_p的乘法逆元，只需要计算其 p-2 次方。在SM2的签名算法中，我们可以应用费马小定理计算

(1 + d_A)^-1 = (1 + d_A)^n-2 mod n

SM2的规范要求私钥的取值范围为 1 ≤ d_A ≤  n-2，因此 1 + d_A 不会为零，也不会为 n 的倍数。

同样地，我们可以应用类似DaA的方法来快速计算 n-2 次方：反复计算乘法和平方（Square and Multiply），估计大约需要256次平方运算和128次乘法运算——精确的结果是256次平方（或255次，如果把第一次节省下来）和187次乘法，因为将 n-2 二进制展开后具有很多的1——其十六进制展开前面是一串F(0b1111)：

0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54121

我们可以把前面的DaA算法简单改造一下（注意每次平方或乘法后需要做一次求模）：

func squareAndMultiply(x, power, mod *big.Int) *big.Int {    out := new(big.Int).SetUint64(1)    for _, bit := range power.bits { //从高位到低位遍历        out.Square(out)        out.Mod(out, mod)        if bit == 1 {            out.Multiply(out, x)            out.Mod(out, mod)        } }    return out}//modInverse(1+dA, n-2, n)给出(1 + dA)^-1

这个算法还能不能进一步优化呢？答案是能。由于 n 为SM2所用椭圆曲线的固定参数，还可以进一步预先将 n-2 分解为较为优化的加法链，从而以更低的运算次数达到同样的效果。目前，高能链使用addchain工具（Michael McLoughlin，项目参见：https://github.com/mmcloughlin/addchain）对 n-2 进行分解，仅需计算253次平方和41次乘法，将所需的乘法运算次数降低为原来的约四分之一（41 : 187）。具体代码比较冗长，为程序所生成，这里就不贴了。未来项目开源后，欢迎各位读者关注。以下仅举一简单例子解释addchain工具的优化作用：

bash-3.2$ addchain search 211addchain: expr: "211"addchain: hex: d3addchain: dec: 211addchain: best: opt(dictionary(sliding_window(4),heuristic(use_first(halving,delta_largest))))addchain: cost: 10_10       = 2*1_11       = 1 + _10_1100     = _11 << 2_1101     = 1 + _1100_11010000 = _1101 << 4return      _11 + _11010000

总的计算代价是10，分别是7次平方和3次乘法以计算x²¹¹：

• 平方得到x²

• 乘法得到x³

• 所得结果连续平方两次得到x¹²

• 乘法得到x¹³

• 所得结果连续平方四次得到x²⁰⁸

• 乘以之前的x³，得到x²¹¹

而如果采用Square and Multiply方法，则211在二进制展开后为11010011，需要8次或7次平方，5次乘法，相较而言约高出20%的计算代价。

此外，以上squareAndMultiply函数还有一个问题在于其Mod运算——并非常数时间，效率也较低；因此虽然总体算法是常数时间的，具体实现却未必。高能链在生产应用中，除了使用addchain工具加以改进以外，底层的大数计算也应用了相关的优化技术，以避免非常数时间且代价昂贵的Mod计算。这也是我们在文章中不提供实际代码而只提供伪代码的原因：既是为了删去无关紧要的技术细节，突出算法重点，也是为了避免这些代码被直接应用于生产环境。

05 总结

素域求逆这个步骤具有一定的计算代价。在高能链的实现中，以上优化过的算法，每次仍然需要消耗大约一万纳秒（在Mac Book Pro M1上实测），约占总的SM2签名时间的18%；而同一测试设备上，扩展欧几里得算法（使用Go的big.Int.ModInverse函数）仅需三千纳秒左右。这是常数时间实现的代价。我们不得不努力在其它方面设法优化，以便最后的签名性能尚能达到较好的水平（实际上，我们在Mac Book Pro M1上小幅超越了谷歌公司BoringSSL的P-256曲线签名性能；而一般来说，由于参数的关系，同等实现技术下SM2具有比P-256更大的计算量。另外，BoringSSL的P-256实现也是常数时间的）。

这是本系列文章关于SM2椭圆曲线算法的最后一篇。关于SM2实现的常数时间技术，到此就介绍完了。在下一篇文章中，我们将探讨SM4算法的常数时间实现。

往期回顾：

常数时间国密算法（一）

常数时间国密算法（二）：SM2的代码分支规避