数学基础
p、q 均为质数
e、d 为正整数,且满足两者的乘积除以p、q的欧拉数,即p、q各自减一后的乘积,余数为1
求证:
对于任意正整数,其e次方除以p、q的欧拉数后的d次方为自身。
有四个正整数,p、q 、e、d ,其中前两个为素数,前两个均大于1,四者满足
e*d=1mod(p-1)(q-1),
则对于任意正整数m,{[(m**e)mod(p-1)(q-1)]**d}mod(p-1)(q-1) = m.
欧拉定理
https://baike.baidu.com/item/欧拉函数/1944850?fr=aladdin
欧拉函数
在数论,对正整数n,欧拉函数是小于n的正整数中与n互质的数的数目(φ(1)=1)。此函数以其首名研究者欧拉命名(Euler's totient function),它又称为Euler's totient function、φ函数、欧拉商数等。 例如φ(8)=4,因为1,3,5,7均和8互质。 从欧拉函数引伸出来在环论方面的事实和拉格朗日定理构成了欧拉定理的证明。
质数又称素数。一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数;否则称为合数。
欧拉函数fi:fi(m),不超过m的正整数中与m互质的数的个数。
phi(1)=1
phi(2)=1
phi(3)=2
phi(4)=2
phi(5)=4
phi(6)=2
注意 :
phi(11)=10
phi(13)=12
phi(17)=16
phi(19)=18
....
phi(113)=112
....
对于素数/质数
phi(p)=p-1
https://baike.baidu.com/item/模反元素/20417595
如果两个正整数a和n互质,那么一定可以找到整数b,使得 ab-1 被n整除,或者说ab被n除的余数是1。这时,b就叫做a的“模反元素”
中文名 模反元素 外文名modulo multiplicative inverse 同义词 模逆元素
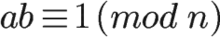
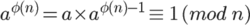
The RSA algorithm involves four steps: key generation, key distribution, encryption and decryption.
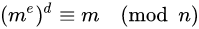
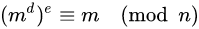
Euler's totient function - Wikipedia https://en.wikipedia.org/wiki/Euler%27s_totient_function
In number theory, Euler's totient function counts the positive integers up to a given integer n that are relatively prime to n. It is written using the Greek letter phi as φ(n) or ϕ(n), and may also be called Euler's phi function. It can be defined more formally as the number of integers k in the range 1 ≤ k ≤ n for which the greatest common divisor gcd(n, k) is equal to 1.[2][3] The integers k of this form are sometimes referred to as totatives of n.
For example, the totatives of n = 9 are the six numbers 1, 2, 4, 5, 7 and 8. They are all relatively prime to 9, but the other three numbers in this range, 3, 6, and 9 are not, because gcd(9, 3) = gcd(9, 6) = 3 and gcd(9, 9) = 9. Therefore, φ(9) = 6. As another example, φ(1) = 1 since for n = 1 the only integer in the range from 1 to n is 1 itself, and gcd(1, 1) = 1.
Euler's totient function is a multiplicative function, meaning that if two numbers m and n are relatively prime, then φ(mn) = φ(m)φ(n).[4][5] This function gives the order of the multiplicative group of integers modulo n (the group of units of the ring ℤ/nℤ).[6] It also plays a key role in the definition of the RSA encryption system.
1>
phi函数
phi(N)为小于正整数N的与N互质的正整数的个数
phi(10)=4
2>
欧拉定理
m(a^phi(n),n)=1
3>
应用
m(7^phi(10),10)=1
==>m(7^4,10)=1
7^222=(7^4)^55*7^2
==>m(7^222,10)=m(1^55,10)*m(7^2,10)=9
Carmichael number - Wikipedia https://en.wikipedia.org/wiki/Carmichael_number
In number theory, a Carmichael number is a composite number 
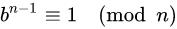
561=3*11*17
m(561-1,3-1)=m(561-1,11-1)=m(561-1,17-1)
1105=5*13*17
m(1105-1,5-1)=m(1105-1,13-1)=m(1105-1,17-1)
In number theory, the Carmichael function associates to every positive integer n a positive integer 
-
for every integer a between 1 and n that is coprime to n.