现实世界中的数据总是“脏的”,主要体现在数据不准确,不完整,不一致,含有噪声和异常等,而数据清洗的目的就是尽可能的使现实中的数据变得准确,完整,一致,真实,可信。
下面逐一讨论如何对存在这些问题数据进行清理。
先从简单的开始:
一 ,数据不完整,即数据中存在缺失值,对于缺失值的处理主要有以下几种方法:
# 删除存在缺失值的记录 , 如果样本数据量比较大,缺失信息较少,删除少量的缺失,是可以接受;但如果样本数据比较大,缺失也比较大的情况,或样本数据量本身比较小,删除缺失的信息对数据挖掘结果来说可能得到不可靠的结论;
# 不处理缺失信息,直接对缺失的数据进行数据挖掘,这可能造成挖掘分析难度大,结论不可靠;
# 填充缺失信息,
1,平均值、众数、中位数进行填充 ; 如数据分布比较均匀,在曲线图上表现为变化比较平缓,可以用均值进行填充;当某一个值在特征向量中出现次数较多,则可以众数填充。
2,使用常数填充,这个需结合实际分析,分析数据间的实际意义;
3,多项式插值:回归插值,拉格朗日插值,牛顿插值法,样条插值
4,KNN 插值(K最近邻),效果不错,补全后的数据不改变分布。推荐大家用,R中实现了一个数据预处理包yaImpute,感兴趣的可以参考
http://www.cnblogs.com/emanlee/archive/2012/12/05/2803144.html
https://www.jstatsoft.org/article/view/v023i10
(目前,考虑在Python中怎么去调用这个包,如果实现了,后面分享出来,大家也可以试下!)
二,数据中存在异常处理方法:
1,通过简单的统计分析,如3σ 准则,数值分布在(μ-3σ,μ+3σ)中的概率为0.9974,可以认为,Y 的取值几乎全部集中在(μ-3σ,μ+3σ)区间内,超出这个范围的可能性仅占不到0.3%。由于落在(μ-3σ,μ+3σ)范围内的概率是很小的,因此可以认为,不在(μ-3σ,μ+3σ)范围内的数据是异常数据。(使用3σ 准则使用前提的,数据统计分布是正态 ,或近似正态,怎么判断正态性?R语言中有一个函数可以近似判断,即:shapiro.test() 可以进行关于正态分布的Shapiro-Wilk检验)

2,箱型图分析
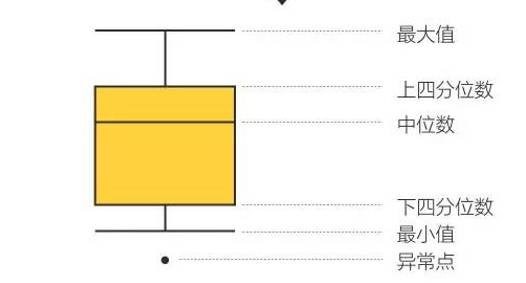
箱型图提供了识别异常值的标准:异常通常被定义为:
小于QL - 1.5IQR 或 大于 QU + 1.5IQR
式中:QL 为下四分位点 , QU 上四分位点 , IQR 分位距 = QU - QL 。
箱型图分析优点:箱型图根据实测数据绘制而成,不要求数据具有特定的统计分布,另一方面,箱型图判断异常值的标准以四分位数和四分位距为基础,四分位数具有一定的鲁棒性:多达25%的数据可以变得任意远而不会很大地扰动四分位数,所以异常值不能对这个标准施加影响。
三,数据中噪声处理
处理方法:分箱;聚类;计算机和人工检查结合;回归
1,分箱
分箱方法是一种简单常用的预处理方法,通过考察相邻数据来确定最终值。所谓“分箱”,实际上就是按照属性值划分的子区间,如果一个属性值处于某个子区间范围内,就称把该属性值放进这个子区间所代表的“箱子”内。把待处理的数据(某列属性值)按照一定的规则放进一些箱子中,考察每一个箱子中的数据,采用某种方法分别对各个箱子中的数据进行处理。在采用分箱技术时,需要确定的两个主要问题就是:如何分箱以及如何对每个箱子中的数据进行平滑处理。
分箱的方法:有4种:等深分箱法、等宽分箱法、最小熵法和用户自定义区间法。
统一权重,也成等深分箱法,将数据集按记录行数分箱,每箱具有相同的记录数,每箱记录数称为箱子的深度。这是最简单的一种分箱方法。
统一区间,也称等宽分箱法,使数据集在整个属性值的区间上平均分布,即每个箱的区间范围是一个常量,称为箱子宽度。
用户自定义区间,用户可以根据需要自定义区间,当用户明确希望观察某些区间范围内的数据分布时,使用这种方法可以方便地帮助用户达到目的。
例:客户收入属性income排序后的值(人民币元):800 1000 1200 1500 1500 1800 2000 2300 2500 2800 3000 3500 4000 4500 4800 5000,分箱的结果如下。
统一权重:设定权重(箱子深度)为4,分箱后
箱1:800 1000 1200 1500
箱2:1500 1800 2000 2300
箱3:2500 2800 3000 3500
箱4:4000 4500 4800 5000
统一区间:设定区间范围(箱子宽度)为1000元人民币,分箱后
箱1:800 1000 1200 1500 1500 1800
箱2:2000 2300 2500 2800 3000
箱3:3500 4000 4500
箱4:4800 5000
用户自定义:如将客户收入划分为1000元以下、1000~2000、2000~3000、3000~4000和4000元以上几组,分箱后
箱1:800
箱2:1000 1200 1500 1500 1800 2000
箱3:2300 2500 2800 3000
箱4:3500 4000
箱5:4500 4800 5000
下面介绍数据平滑方法:
⑴按平均值平滑
对同一箱值中的数据求平均值,用平均值替代该箱子中的所有数据。
⑵按边界值平滑
用距离较小的边界值替代箱中每一数据。
⑶按中值平滑
取箱子的中值,用来替代箱子中的所有数据。
2,聚类:将物理的或抽象对象的集合分组为由类似的对象组成的多个类。
找出并清除那些落在簇之外的值(孤立点),这些孤立点被视为噪声。
3,回归;试图发现两个相关的变量之间的变化模式,通过使数据适合一个函数来平滑数据,即通过建立数学模型来预测下一个数值,包括线性回归和非线性回归。
总结
这些方法并不是万能,现实世界的复杂多样,我们需要针对具体情况具体分析,选择合适的方法,提高数据质量,以保证得到可靠的数据挖掘结论。
参考
http://blog.csdn.net/lizhengnanhua/article/details/8982968