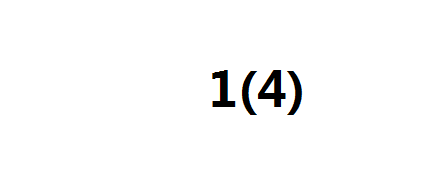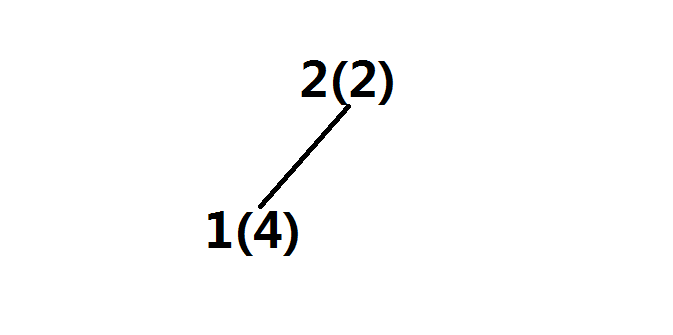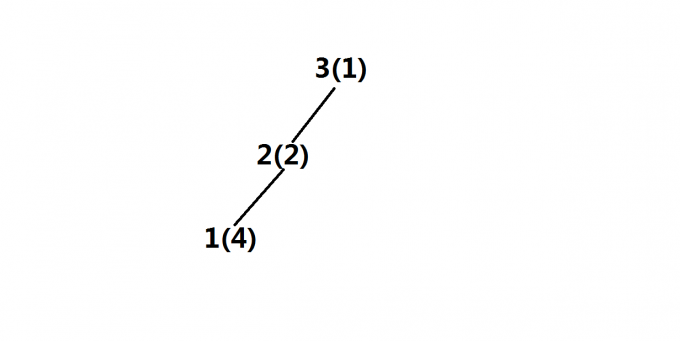洛谷 P1377 [TJOI2011]树的序 (单调队列优化建BST
题意分析
本题思路很简单,根据题意,我们利用所给的Bst生成序将Bst建立起来,然后输出该BST的先序遍历即可;
但,如果我们不加优化,建BST的时间复杂度在最劣情况下将达到O(n^2),显然,在1e5的数据下是过不去的,所以我们考虑利用利用单调队列优化来建BST;
算法思路
BST建树本质上便是按照权值将新加入节点插入到对应的位置,该过程受插入顺序
影响
我们考虑可以将读入的生成序列的下标变成权值,本身权值变为下标
for(int i=1;i<=n;i++){
x=read();
a[x]=i;
}
因为权值为1-n的序列,我们将该数组从1-n遍历,本质便是按权值从小到大遍历(如
果权值不是1-n的序列,将其离散化即可)
我们按该方式维护一个单调队列,当一个新数进队列后不在向前更新时,我们便将
该节点插到单调队列中它左侧节点的右子树中,原因很简单,该节点左侧的节点先
入队列,说明左侧权值一定比该节点小,故将该点插入到左侧节点的右子树上,假设
该节点进队列过程中压掉了节点,则将该节点插入到被它压掉的最后一个节点的左
子树上,我们用此方法便可以在O(n)的时间复杂度下建成一颗bst了,建树代码如下
int tot=0;
int pos=0;
for(int i=1;i<=n;i++){
tot=pos;
while(pos&&a[q[pos]]>a[i]){
pos--;
}
if(pos){
r[q[pos]]=i;
}
if(pos<tot){
l[i]=q[pos+1];
}
q[tot=++pos]=i;
}
为什这样建树可以建出正确的bst呢?
我们举个例子
比如3 2 4 1这个序列
排序后变为了1(4) 2(2) 3(1) 4(3)
括号内为权值,括号外为下标
第一步,插入1(4)
第二步,插入2(2)因为在单调队列中我们将其压掉了所以,将1(4)a插入到2(2)的左子树中
第三步
同理
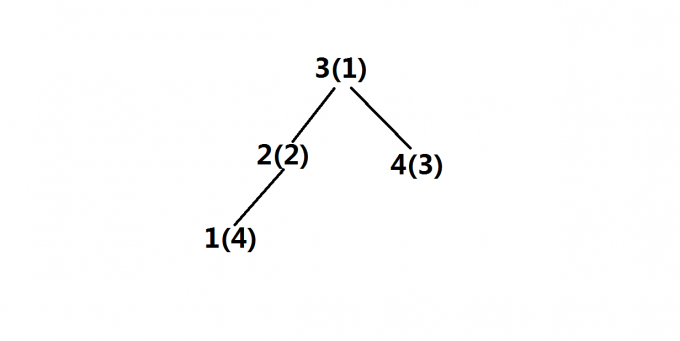
第四步,目前单调队列中只有3(1)新点4(3)进入后无法压掉3(1)便放在3(1)的左子树中
建树完毕,我们按权值加入,每进入一个点便插入到目前的合适位置,当更优的点
出现时,倘若恰好将此点压掉,我们便将上一个点与该点的连接关系断开,将新节
点插入到这两个节点之间,如下图
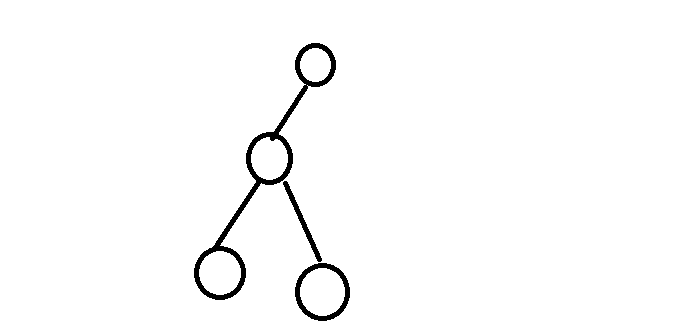
红色为新加入节点
为什么后续加入的节点不会插到以经压入的节点下呢?得益于我们加入节点是按权值从小到大加入的
比如说上图,既然红色节点已经入队列了,能红色节点的子树中插入的节点一定小于红色节点的权值,但已经没有了
这就是整个算法的思路
完整代码如下
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
const int maxn=1e6+10;
inline int read(){
int ret=0;
int f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-'){
f=-f;
}
ch=getchar();
}
while(ch>='0'&&ch<='9'){
ret=ret*10+(ch^'0');
ch=getchar();
}
return ret*f;
}
int q[maxn];
int l[maxn];
int r[maxn];
int a[maxn];
int n;
void dfs(int ro){
if(!ro){
return ;
}
cout<<ro<<" ";
dfs(l[ro]);
dfs(r[ro]);
return ;
}
int main(){
n=read();
int x;
for(int i=1;i<=n;i++){
x=read();
a[x]=i;
}
int tot=0;
int pos=0;
for(int i=1;i<=n;i++){
tot=pos;
while(pos&&a[q[pos]]>a[i]){
pos--;
}
if(pos){
r[q[pos]]=i;
}
if(pos<tot){
l[i]=q[pos+1];
}
q[tot=++pos]=i;
}
dfs(q[1]);
return 0;
}
完结撒花!