杨辉三角

杨辉三角

形如以下为杨辉三角

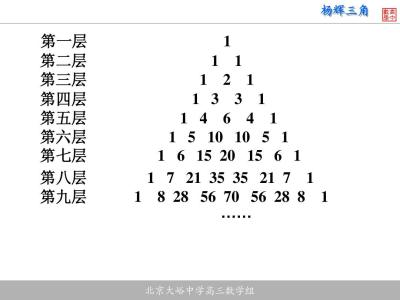
杨辉三角有很多性质，我们用以下两种简单的性质来用python实现。

1第n行的数字有n项。

2每个数等于它上方两数之和.

n=6
trangle = [[1]]
for i in range(1,n):
    pre=trangle[i-1]
    cur=[1]
    trangle.append(cur)
    for j in range(i-1):
        cur.append(pre[j]+pre[j+1])
    cur.append(1)
print(trangle)

 这是最简单的一种方法，关键在于控制边界方法就是不断的代入测试，只要前两遍也就是第三行和第四行可以实现，后边就应当能够实现，第一二行可以先特殊对待，在程序实现后，在回头扩宽边界。

 除了以1为边界外，还可以在两侧补零

n=6
#######杨辉三角两侧补零
l=[[1]]
for i in range(1,n):
    pre=[0]+l[i-1]+[0]
    cur=[]
    l.append(cur)
    for j in range(i+1):
        cur.append(pre[j]+pre[j+1])
print(l)

两侧补零在左侧补零会频繁调动列表移动，更好的办法是在右侧补零，最左边的索引为0的值为上一列的索引为-1和0的两项的和，也就是0+1刚好是1，需要注意的也是边界问题，如下

##杨辉三角右侧补零
n=6
l=[[1]]
for i in range(1,n):
    pre=l[i-1]+[0]
    cur=[]
    l.append(cur)
    for j in range(i+1):
        cur.append(pre[j-1]+pre[j])
print(l)

杨辉三角是一个轴对称图形，可以在计算时只计算左侧的数值，在数据量变大时，可以提高效率。

这里使用先建立一个列表，n个1，n是要求到的行数。使用

n=6
l=[[1]]
for i in range(1,n):
    p=l[i-1]
    c=[1]*(i+1)
    for j in range(0,i//2):
        value=p[j]+p[j+1]
        c[j+1]=value
        if i!=2j:
            c[-j-2]=value
    l.append(c)
print(l)

使用两个列表相互循环

%%timeit
m=20
k=7

for i in range(m):
    newline=[1]*(i+1)
    e=i//2
    for j in range(e):
        newline[j+1]=oldline[j]+oldline[j+1]
        if j!=e:
            newline[-j-2]=newline[j+1]
    oldline=newline
    
#print(newline)

输出      30.2 µs ± 327 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)

使用一个列表实现

这里使用先建立一个列表，n个1，n是要求到的行数。使用list[:3],表示取出从0到3的元素，循环取出打印，最后列表只保留最后的一行数据

n=6
lst=[1]*n
for i in range(n):
    e=i//2
    tmp=1
    offset=n-i
    for j in range(1,e+1):
        value=tmp+lst[j]
        tmp=lst[j]
        lst[j]=value
        if i != 2j:
            lst[-j-offset]=value
    print(lst[:i+1])

 输出　　23.1 µs ± 323 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)

使用一个列表或的思想是生产中，对于能知道范围的数据，提前建立足够用的列表，在后期的使用中足够用，能用替换就少用append，能不遍历就不遍历。

使用一个列表减少了空间复杂度，但是时间复杂度并未减少，应当注意在列表值增大后，在每次列表更新后，原来的列表只是没有了引用计数，但并未消失，在内存中变成了内存垃圾。在技算量达到极高的量级时，每次产生的垃圾都会对内存造成冲击，如果此时，python的GC（垃圾处理）会停止其他一切内存活动，只进行垃圾处理，内存空间的整理，此时可能产生的问题是，内存没有足够的空间存放你的下一个列表，它会挪动你当前的列表，效率问题及大。

解决方案是优化算法，将庞大的列表分成一个个小的部分进行处理。

一旦数据量增大，要时刻注意效率问题。

在内存中，一旦内存使用率到达一定阈值，会触发python的自动的垃圾回收，在对垃圾回收没有足够的了解时，不要手动垃圾回收，会对系统造成性能影响。

通项公式的解法

C(n-1,m-1)=(n-1)!/[(m-1)!(n-m)!]

解法

####trangle.2
while True:
    m = input('m=')
    if str.isdigit(m):
        m = int(m)
        k = input('k=')
        if str.isdigit(k):
            k = int(k)
            if k > m:
                print('k<=m only')
            else:
                 break
        else:
            print('numbre only')
    else:
        print('numbre only')
a = 1
b = 1
c = 1
e = m - k
for i in range(1,m):
    a *= i
    if i == k - 1:
        b = a
    if i == e:
        c = a
print(int(a / (b * c)))

取消上半部输入程序，输出为　　2.25 µs ± 47.6 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

使用相同的算法，将列表引入，如下

%%timeit
n=20
lst=[1]*n
for i in range(n):
    e=i//2
    tmp=1
    offset=n-i
    for j in range(1,e+1):
        value=tmp+lst[j]
        tmp=lst[j]
        lst[j]=value
        if i != 2j:
            lst[-j-offset]=value
   # print(lst[:i+1])

输出　　2.43 µs ± 36 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

以上所用算法中，在单独求某一行，某一位时，使用通项公式速度较快，在使用列表时，调用了append函数，速度比直接赋值给标识符慢一点，可能原因是append函数导致的。

在计算某一行或者打印杨辉三角时，耗时较接近，使用对称的性质时在相应方法内效率较高。