xgboost原理及应用--转
1.背景
关于xgboost的原理网络上的资源很少,大多数还停留在应用层面,本文通过学习陈天奇博士的PPT地址和xgboost导读和实战 地址,希望对xgboost原理进行深入理解。
2.xgboost vs gbdt
说到xgboost,不得不说gbdt。了解gbdt可以看我这篇文章 地址,gbdt无论在理论推导还是在应用场景实践都是相当完美的,但有一个问题:第n颗树训练时,需要用到第n-1颗树的(近似)残差。从这个角度来看,gbdt比较难以实现分布式(ps:虽然难,依然是可以的,换个角度思考就行),而xgboost从下面这个角度着手
注:红色箭头指向的l即为损失函数;红色方框为正则项,包括L1、L2;红色圆圈为常数项。
利用泰勒展开三项,做一个近似,我们可以很清晰地看到,最终的目标函数只依赖于每个数据点的在误差函数上的一阶导数和二阶导数。
3.原理
(1)定义树的复杂度
对于f的定义做一下细化,把树拆分成结构部分q和叶子权重部分w。下图是一个具体的例子。结构函数q把输入映射到叶子的索引号上面去,而w给定了每个索引号对应的叶子分数是什么。
定义这个复杂度包含了一棵树里面节点的个数,以及每个树叶子节点上面输出分数的L2模平方。当然这不是唯一的一种定义方式,不过这一定义方式学习出的树效果一般都比较不错。下图还给出了复杂度计算的一个例子。
注:方框部分在最终的模型公式中控制这部分的比重
在这种新的定义下,我们可以把目标函数进行如下改写,其中I被定义为每个叶子上面样本集合
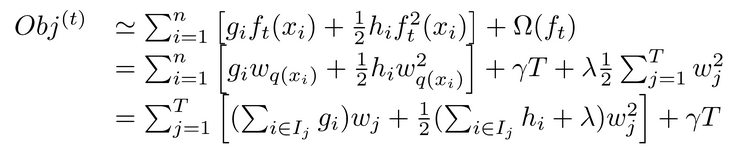
这一个目标包含了TT个相互独立的单变量二次函数。我们可以定义
最终公式可以化简为

通过对

然后把

(2)打分函数计算示例
Obj代表了当我们指定一个树的结构的时候,我们在目标上面最多减少多少。我们可以把它叫做结构分数(structure score)
(3)枚举不同树结构的贪心法
贪心法:每一次尝试去对已有的叶子加入一个分割

对于每次扩展,我们还是要枚举所有可能的分割方案,如何高效地枚举所有的分割呢?我假设我们要枚举所有x < a 这样的条件,对于某个特定的分割a我们要计算a左边和右边的导数和。

我们可以发现对于所有的a,我们只要做一遍从左到右的扫描就可以枚举出所有分割的梯度和GL和GR。然后用上面的公式计算每个分割方案的分数就可以了。
观察这个目标函数,大家会发现第二个值得注意的事情就是引入分割不一定会使得情况变好,因为我们有一个引入新叶子的惩罚项。优化这个目标对应了树的剪枝, 当引入的分割带来的增益小于一个阀值的时候,我们可以剪掉这个分割。大家可以发现,当我们正式地推导目标的时候,像计算分数和剪枝这样的策略都会自然地出现,而不再是一种因为heuristic(启发式)而进行的操作了。
4.自定义损失函数
在实际的业务场景下,我们往往需要自定义损失函数。这里给出一个官方的 链接 地址
5.Xgboost调参
由于Xgboost的参数过多,使用GridSearch特别费时。这里可以学习下这篇文章,教你如何一步一步去调参。地址
6.python、R对于xgboost的简单使用
任务:二分类,存在样本不均衡问题(scale_pos_weight可以一定程度上解读此问题)
【Python】
【R】
7.xgboost中比较重要的参数介绍
(1)objective [ default=reg:linear ] 定义学习任务及相应的学习目标,可选的目标函数如下:
- “reg:linear” –线性回归。
- “reg:logistic” –逻辑回归。
- “binary:logistic” –二分类的逻辑回归问题,输出为概率。
- “binary:logitraw” –二分类的逻辑回归问题,输出的结果为wTx。
- “count:poisson” –计数问题的poisson回归,输出结果为poisson分布。 在poisson回归中,max_delta_step的缺省值为0.7。(used to safeguard optimization)
- “multi:softmax” –让XGBoost采用softmax目标函数处理多分类问题,同时需要设置参数num_class(类别个数)
- “multi:softprob” –和softmax一样,但是输出的是ndata * nclass的向量,可以将该向量reshape成ndata行nclass列的矩阵。没行数据表示样本所属于每个类别的概率。
- “rank:pairwise” –set XGBoost to do ranking task by minimizing the pairwise loss
(2)’eval_metric’ The choices are listed below,评估指标:
- “rmse”: root mean square error
- “logloss”: negative log-likelihood
- “error”: Binary classification error rate. It is calculated as #(wrong cases)/#(all cases). For the predictions, the evaluation will regard the instances with prediction value larger than 0.5 as positive instances, and the others as negative instances.
- “merror”: Multiclass classification error rate. It is calculated as #(wrong cases)/#(all cases).
- “mlogloss”: Multiclass logloss
- “auc”: Area under the curve for ranking evaluation.
- “ndcg”:Normalized Discounted Cumulative Gain
- “map”:Mean average precision
- “ndcg@n”,”map@n”: n can be assigned as an integer to cut off the top positions in the lists for evaluation.
- “ndcg-“,”map-“,”ndcg@n-“,”map@n-“: In XGBoost, NDCG and MAP will evaluate the score of a list without any positive samples as 1. By adding “-” in the evaluation metric XGBoost will evaluate these score as 0 to be consistent under some conditions.
(3)lambda [default=0] L2 正则的惩罚系数
(4)alpha [default=0] L1 正则的惩罚系数
(5)lambda_bias 在偏置上的L2正则。缺省值为0(在L1上没有偏置项的正则,因为L1时偏置不重要)
(6)eta [default=0.3]
为了防止过拟合,更新过程中用到的收缩步长。在每次提升计算之后,算法会直接获得新特征的权重。 eta通过缩减特征的权重使提升计算过程更加保守。缺省值为0.3
取值范围为:[0,1]
(7)max_depth [default=6] 数的最大深度。缺省值为6 ,取值范围为:[1,∞]
(8)min_child_weight [default=1]
孩子节点中最小的样本权重和。如果一个叶子节点的样本权重和小于min_child_weight则拆分过程结束。在现行回归模型中,这个参数是指建立每个模型所需要的最小样本数。该成熟越大算法越conservative
取值范围为: [0,∞]
更多关于Xgboost学习地址







