决策树是一类常见的分类算法,它思路清晰简单,实现也并不困难。正如其名,决策树是基于树状结构来决策的。《机器学习》中有一个例子,按决策树的来判断“这是一个好的西瓜吗?”,首先,我们要看看西瓜的纹理,如果纹理清晰,我们再看它的根蒂是否蜷缩,色泽是否青绿,触感是否硬滑....如果都是,那它大概率是一颗好瓜。画成图大概如下:
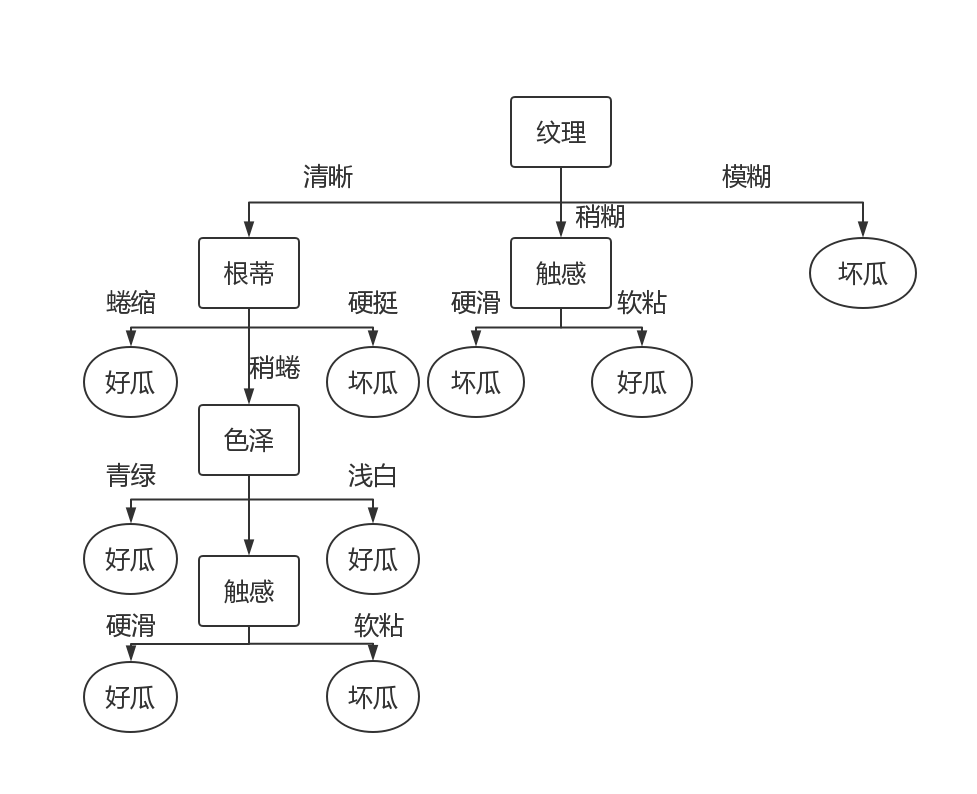
显然地,决策树的每个分支都是对某个属性的测试,而测试的结果将会导出结果、或者进一步的测试。一般的,一颗决策树包含一个根结点、若干个内部节点和叶节点;由根到叶,组成了一条测试序列,叶是测试结果,根和内部节点是测试属性。通过培养一颗决策树,我们就可以对数据进行有效的分类。接下来我们看看西瓜书上的算法图:

类别C表示分类结果(如好瓜),Dv表示按属性a的取值划分出的子集(如触感=硬滑的瓜)
要注意的是,这里的三条递归终止条件:
(1)样本全为同一类别;
(2)属性集空或者样本在属性集上取值一致;
(3)分支节点为空。这三条必须全都满足,不然在生成树的时候,要么准确率低,要么出错。
决策树的重点就在于第八行的选取划分属性,其余的步骤都是基本一直的。简单来讲,入门决策树的划分选择有三:
(1)信息增益(或称熵减,即id3);
(2)信息增率(即c4.5);
(3)基尼指数(数据纯度,即cart)。
(1)id3
id3的划分基于信息熵(香农熵),熵越大的数据,其不纯的程度也就越大,相反,熵越小的数据,其纯度也就越高,换言之,更为有条理(比方说根蒂蜷缩的西瓜大多是好瓜)。而id3(基于熵减的划分),就是寻找能够在最大程度上降低熵的划分属性,从而达到提高数据纯度的目的(分类也就越准确)。
熵计算公式:

信息增益公式:
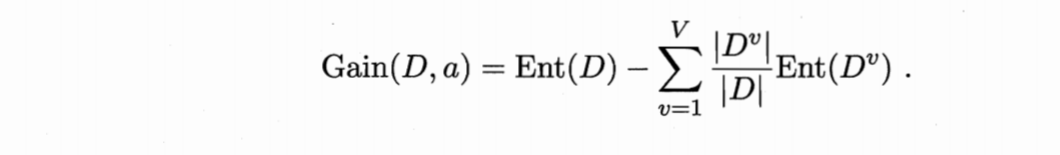
|D|表示数据集的数据个数(模)
在id3中,只需遍历A中的所有可划分的属性,选择gain最大的那一个属性来划分即可。
(2)c4.5
上文所说的id3在使用时会有一个问题,就是它会倾向于那些可取值较多的属性(划分完之后生成若干个小子集),即它更倾向于数量(属性中可能的取值数)而非质量(属性中单个取值的熵减)。c4.5就是倾向于质量的划分选择。
具体公式如下:
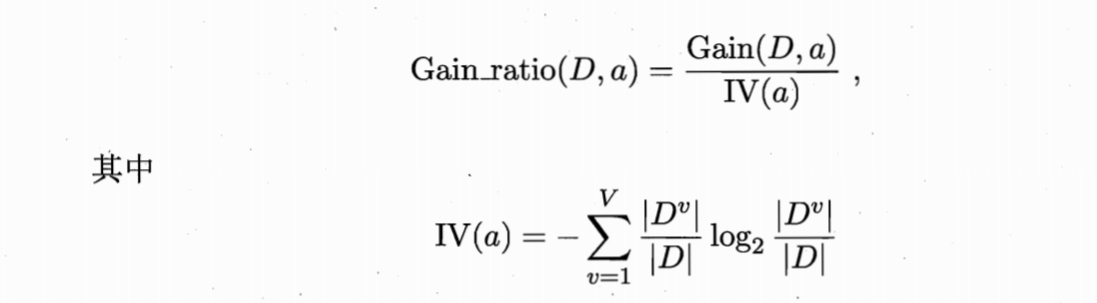
不过,c4.5也并非只注重于信息增率(增率),它是现在信息增量高于平均水平的属性中,找出增率最大的那一个,所以既兼顾了数量也兼顾了质量。
(3)cart
cart方法与上面两种都不太类似,它用了一种称为“基尼指数”的标准来划分属性,如下:
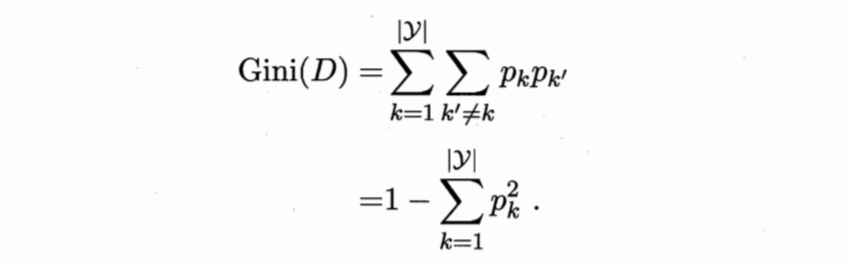
Pk为类别为k的数据的概率(好瓜比例),按上面的公式,基尼指数表示任意选两个样本,其类别不一致的概率,即一个集合里面数据不纯的程度。
如果加上权重,那么基尼指数如下:
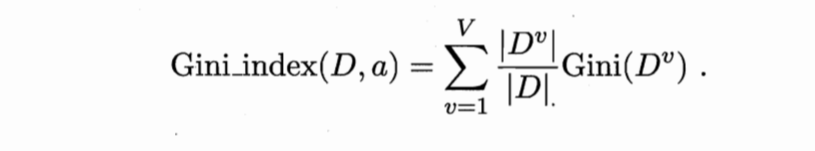
即划分时选取基尼指数最小的那一个属性。
决策树的代码和测试数据等我推到github上再贴出来。
以上是三种比较常见的决策树,但这三种决策树的效果还可以进一步再优化,有两种思路:
(1):进行剪枝,增强泛化能力;
(2):集成,用RF、Adaboost等算法来增强泛化能力和准确率。
下一步我打算写一写关于决策树在集成算法方面的应用。