一般定义:将一组“无序”的数据元素调整为“有序”的数据元素。
数学定义:假设含n个数据元素的序列为{R1,R2,...,Rn},其相应的关键字序列为{K1,K2,...,Kn},这些关键字相互之间可以进行比较,即在它们之间存在这样的关系:

按此固有关系将上式记录序列重新排序为:
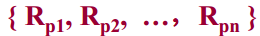
的操作称为排序。
排序的稳定性:

稳定排序示例:

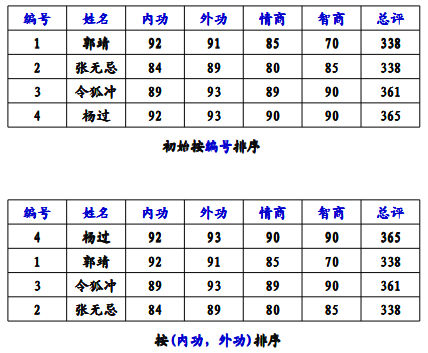
多关键字排序:
排序时需要比较的关键字多余一个。
- 排序时首先按照关键字1进行排序
- 当关键字1相同时按照关键字2进行排序
- ......
- 当关键字n-1相同时,按照关键字n进行排序
示例:
排序中的关键操作:
1. 比较:任意两个数据元素通过比较确定先后顺序
2. 交换:数据元素之间需要交换才能得到预期的结果
内排序和外排序:
1. 内排序:整个排序过程不需要访问外存便能完成。
2. 外排序:待排序的数据元素数量很大,整个序列的排序过程不可能在内存中完成。
排序的审判:
1. 时间性能:
关键性能差异体现在比较和交换的数量
2. 辅助空间性能:
为完成排序操作需要的额外的存储空间
必要时可以“空间换时间”
3. 算法的实现复杂性:
过于复杂的排序算法会影响代码的可读性和可维护性,也可能影响排序的性能
小结:
1. 排序时数据元素从无序到有序的过程
2. 排序具有稳定性,是选择排序算法的因素之一
3. 比较和交换时排序的基本操作
4. 多关键字排序与单关键字排序无本质区别
5. 排序的时间性能是区分排序算法好坏的主要因素