向量化编程实现
Vectorized implementation
一向量化编程 Vectorization
1.1 基本术语
向量化 vectorization
1.2 向量化编程（Vectorization）
向量化编程是提高算法速度的一种有效方法。为了提升特定数值运算操作（如矩阵相乘、矩阵相加、矩阵-向量乘法等）的速度，数值计算和并行计算的研究人员已经努力了几十年。矢量化编程的思想就是尽量使用这些被高度优化的数值运算操作来实现我们的学习算法。
代码中尽可能避免显式的for循环。
刚开始编写程序的时候，你可能会选择不使用太多矢量化技巧来实现你的算法，并验证它是否正确（可能只在一个小问题上验证）。在确定它正确后，你可以每次只矢量化一小段代码，并在这段代码之后暂停，以验证矢量化后的代码计算结果和之前是否相同。最后，你会有望得到一份正确的、经过调试的、矢量化且有效率的代码。
二逻辑回归的向量化实例 Logistic Regression Vectorization Example
2.1 基本术语
逻辑回归 Logistic Regression
批量梯度上升法 batch gradient ascent
对数似然函数 the log likelihood
2.2逻辑回归向量化实现
对logistic回归分析模型进行训练，其模型如下：
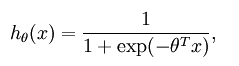
其中，我们需要如下计算梯度：
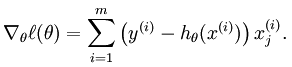
我们用Matlab/Octave风格变量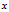
表示输入数据构成的样本矩阵，
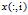代表第
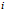个训练样本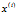
，
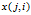就代表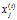
（译者注：第
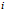个训练样本向量的第
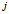个元素，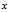
是一个矩阵）。同样，用Matlab/Octave风格变量
表示由训练样本集合的全体类别标号所构成的行向量，则该向量的第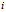
个元素
就代表上式中的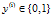
。
最容易写出来的梯度运算代码：
两层循环，速度极慢。对算法进行部分向量化，去掉嵌套的循环。
还可以使效率更高，假定b是一个列向量，A是一个矩阵，我们用以下两种方式来计算A*b：
将b(i)看成(y(i) - sigmoid(theta'*x(:,i)))，A看成x，我们就可以使用以下高效率的代码：
三神经网络向量化 Neural Network Vectorization
3.1 基本术语
训练样本 training examples
稀疏自编码网络 sparse autoencoder
稀疏惩罚 sparsity penalty
平均激活率 average firing rate
3.2 正向传播向量化版本（Forward propagation）
考虑一个三层网络（一个输入层、一个隐含层和一个输出层），并且假定x是包含一个单一训练样本
的列向量。则向量化的正向传播步骤如下：
但是当我们需要处理m个训练样本时，我们可以利用并行化和高效矩阵运算的优势，使用向量来处理多个训练样本。
repmat(b1,1,m)的运算效果是，它把列向量b1拷贝m份，然后堆叠成如下矩阵：
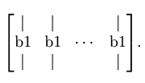
Sigmoid激活函数向量化实现：
3.3 反向传播向量化版（Backpropagation）
对于监督学习，我们有一个包含m个带类别标号样本的训练集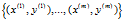
。假定网络的输出有s3维，因而每个样本的类别标号向量就记为
。
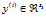现在我们要计算梯度项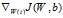
和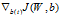
。对于每个训练样本(x,y)，我们可以这样来计算：
在这里
表示对两个向量按对应元素相乘的运算（译者注：其结果还是一个向量）。为了描述简单起见，我们这里暂时忽略对参数b(l)的求导，不过在你真正实现反向传播时，还是需要计算关于它们的导数的。
反向传播的非向量化版本可如下实现：
我们还要实现一个函数fprime(z)，该函数接受矩阵形式的输入z，并且对矩阵的按元素分别执行
。
3.4 稀疏自编码网络（Sparse autoencoder）
稀疏自编码网络中包含一个额外的稀疏惩罚项，目的是限制神经元的平均激活率，使其接近某个（预设的）目标激活率ρ。其实在对单个训练样本上执行反向传播时，我们已经考虑了如何计算这个稀疏惩罚项，如下所示：
在非向量化的实现中，计算代码如下：
