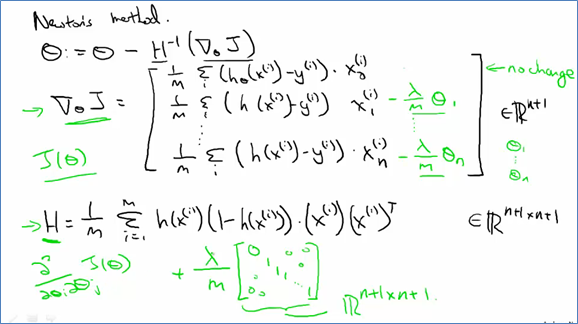基础知识ML
在进行深度学习前，根据学习网站的建议，首先学习机器学习的基础课程，学习资料主要是Andrew讲的ShortVideo，网址：http://openclassroom.stanford.edu/MainFolder/CoursePage.php?course=DeepLearning。下面是这些基础课程的学习笔记。
一线性回归I（Linear Regression I）
1.1 监督学习介绍 Supervised Learning Intro
首先对监督学习进行简单介绍，其中包括回归（Regreesion）和分类（Classification）两个问题。
回归问题：根据训练集可以给出线性函数，然后对输入进行预测，结果是实数值。
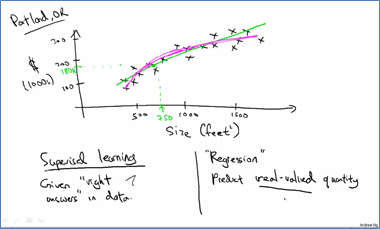
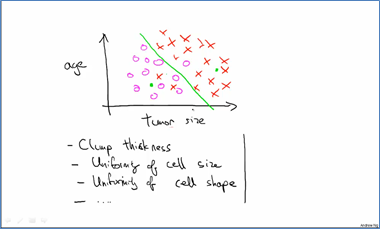
分类问题：根据训练集可以进行划分，对输入进行分类，结果一般是整数（属于哪个类别）。
1.2 模型表达 Model Representation
在有训练数据的情况下，我们要对新的输入进行预测，得到输出，就需要对这个问题进行建模来加以预测，对于一个问题，我们要进行数学描述，模型表达就是将我们的问题形式化，给出输入和输出的函数关系式，可以用矩阵表示。
1.3 损失函数 Cost Function
损失函数是训练样本的平均相关误差函数，通常我们根据损失函数来求解模型表达式中的参数，目标是使损失函数最小。常用的损失函数如下：
（1）0-1损失函数
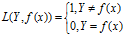
（2）平方损失函数
（3）绝对损失函数
（4）对数损失函数
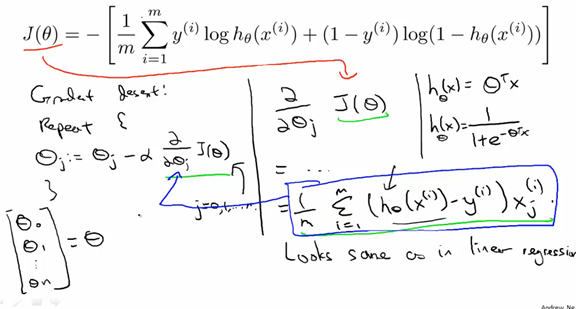
1.4 梯度下降法Gradient Descent
梯度下降法常用来求解模型的参数，即求损失函数最小值。他的核心思想就是沿着损失函数最陡的方向下降，每轮改变损失函数的所有参数，直到损失函数达到最小值。参数改变是通过对损失函数求偏导而得：
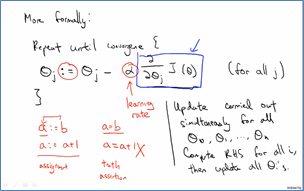
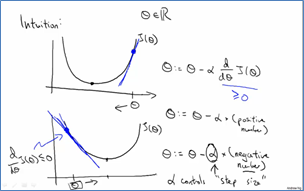
学习速率α不能太小，否则下降的速度十分慢，α也不能太大，否则会超越目标，找不到最小值。
在线性回归问题中我们就可以用梯度下降法来求回归方程中的参数。有时候该方法也称为批量梯度下降法，这里的批量指的是每时刻参数的更新使用到了所有的训练样本。
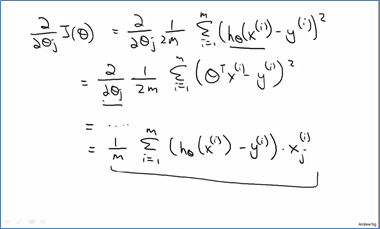
1.5 向量实现 Vectorized Implementation
在实际问题中很多变量都是向量的，所有如果要把每个分量都写出来的话会很不方便，应该尽量写成向量的形式。Vectorized Implementation指的是向量实现，上面的梯度下降法的参数更新公式可以用向量形式实现的。向量形式的公式简单，且易用matlab编程。
二线性回归II （Linear Regression II）
2.1 数据规范化 Feature Scaling
Feature scaling (数据规范化) 是数据挖掘或机器学习常用到的步骤，这个步骤有时对算法的效率和准确率都会产生巨大的影响。例如在机器学习中，如果包含两个特征，一个的取值范围为[50000,70000]，而另一个特征取值范围为[20,100]，那么特征一将会大大影响到特征二，所以需要进行特征规范化，将他们放缩到一个相近的范围。
在梯度下降法中，由于梯度下降法是按照梯度方向来收敛到极值的，如果输入样本各个维数的尺寸不同（即范围不同），则这些参数的构成的等高线不同的方向胖瘦不同，这样会导致参数的极值收敛速度极慢。因此在进行梯度下降法求参数前，需要进行feature scaling
Feature scaling的一般方法：
其中a可以是特征X的均值，b可以为x的最大值、（最大值-最小值）、标准差等。
2.2 学习速率 Learning Rate
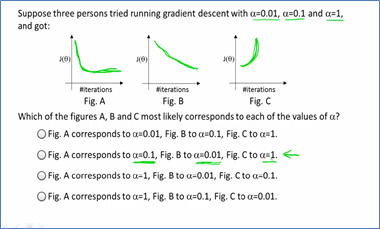
接下来就是学习率对梯度下降法的影响。如果学习速率过大，这每次迭代就有可能出现超调的现象，会在极值点两侧不断发散，最终损失函数的值是越变越大，而不是越来越小。如果学习速率太小，则该曲线下降得很慢，甚至在很多次迭代处曲线值保持不变。那到底该选什么值呢？这个一般是根据经验来选取的，比如从…0.0001,0.001,.0.01,0.1,1.0…这些参数中选，看那个参数使得损失值和迭代次数之间的函数曲线下降速度最快。
2.3 特征和多项式回归 Features and Polynomial Regression
同一个问题中我们可以选用不同的特征，比如单个面积特征其实是可以写成长和宽两个特征的。在使用多项式拟合模型时，不同的特征模型也会有所不同，每一项其实都代表着一个特征。
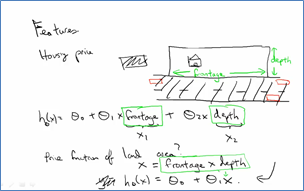
2.4 正规方程 Normal Equations
当用训练样本来进行数据的测试时，一般都会将所有的训练数据整理成一个矩阵，矩阵的每一行就是一个训练样本，这样的矩阵也叫做"design matrix"。下面的矩阵X就是
当用矩阵的形式来解多项式模型的参数时，我们希望
，进行求解：
（因为要求逆，所以要先转成方阵）
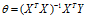这个方程也称为normal equations.
Normal Equation 跟 Gradient Descent一样，可以用来求权重向量θ。但它与Gradient Descent相比，既有优势也有劣势。优势：Normal Equation可以不在意x特征的scale。劣势：相比于Gradient Descent，Normal Equation需要大量的矩阵运算，特别是求矩阵的逆。在矩阵很大的情况下，会大大增加计算复杂性以及对计算机内存容量的要求。
虽然
是方阵，但是它的逆不一定存在（当一个方阵的逆矩阵不存在时，该方阵也称为sigular）。比如说当X是单个元素0时，它的倒数不存在，这就是个Sigular矩阵，当然了这个例子太特殊了。另一个比较常见的例子就是参数的个数比训练样本的个数还要多时也是非可逆矩阵。这时候要求解的话就需要引入regularization项，或者去掉一些特征项redundant feature（典型的就是降维，去掉那些相关性强的特征）。
三逻辑回归（Logistic Regression）
3.1 分类 Classification
上面讲的函数一般都是回归方面的，也就是说预测值是连续的，如果我们需要预测的值只有2种，要么是要么不是，即预测值要么是0要么是1，那么就是分类问题了。
3.2 模型 Model
我们需要有一个函数将原本的预测值映射到0到1之间，通常这个函数就是logistic function，或者叫做sigmoid function。因为这种函数值还是个连续的值，所以对logistic函数的解释就是在给定x的值下输出y值为1的概率。
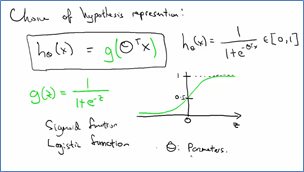
3.3 优化目标 Optimization Objective
现讨论损失函数的优化。首先损失函数应该是一个convex函数，即只有一个极值点，而不是non-convex函数，它存在很多极值点。
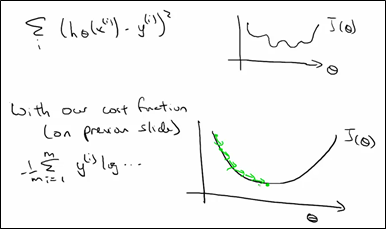
在线性回归中，我们使用平方差来当做损失函数。
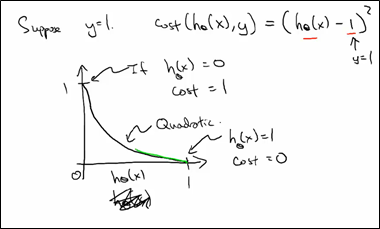
对于损失函数，我们希望训练集中标签值为1的那些样本集，损失函数要求我们当预测值为1时，损失函数值最小（为0），当便签值为0时，此时损失函数的值最大。
对于这样的函数我们可以用log函数来当做损失函数。
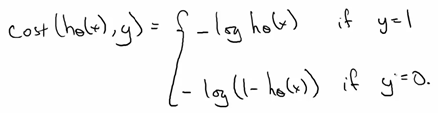
我们可以将上面的损失函数进行整合：
平方差的损失函数求和后是non-convex的而log损失函数是convex的
3.4 梯度下降法GradientDescent
3.5 牛顿法Newton's Method
也就是求
的导数
，即最小值，令
，下面使用牛顿法求：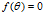
。当
（很小的值）停止迭代，得到参数值。
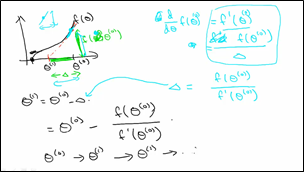
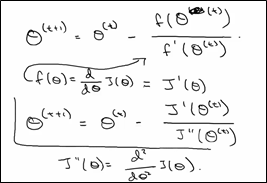
上面是在二维的情况下，如果在多维的情况下，其中H是hessian矩阵（多元函数的二阶偏导数构成的方阵）
3.6 梯度下降VS牛顿法Gradient Descent vs Newton's Method
梯度下降法有参数学习速率，它需要更多次的迭代，不过每次迭代的复杂度是O(n)；牛顿法没有参数，它需要较少次的迭代，不过每次迭代的时间复杂度是O(n3)，当特征数比较多的时候我们应该选择梯度下降法，因为牛顿法每轮的计算量太大。
N的大小规定大致划分如下：
四正则化（Regularization）
4.1 过拟合问题The Problem of Overfitting
如果当系统的输入特征有多个，而系统的训练样本比较少时，这样就很容易造成over-fitting的问题。这种情况下要么通过降维方法来减小特征的个数（也可以通过模型选择的方法），要么通过regularization的方法，通常情况下通过regularization方法在特征数很多的情况下是最有效，但是要求这些特征都只对最终的结果预测起少部分作用。
4.2 优化目标 Optimization Objective
规则项可以作用在参数上，让最终的参数很小，当所有参数都很小的情况下，这些假设就是简单假设（简单假设是指零假设的参数集合仅仅包含一个元素的假设。），从而能够不是很倾向于over-fitting的问题。一般对参数进行regularization时，前面都有一个惩罚系数，这个系数称为regularization parameter，如果这个规则项系数太大的话，有可能导致系统所有的参数最终都很接近0，所有会出现欠拟合的现象。
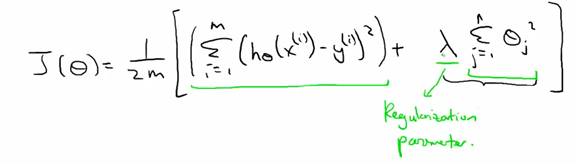
4.3 规则项形式Common Variations
在多元线性回归中，规则项一般惩罚的是参数1到n（当然有的也可以将参数0加入惩罚项，但不常见）。随着训练样本的增加，这些规则项的作用在慢慢减小，因此学习到的系统的参数倾向而慢慢增加。规则项还有很多种形式，如L2-norm regularization(或者叫做2-norm regularization).当然了，还有L1-norm regularization。由于规则项的形式有很多种，所以这种情形也称为规则项的common variations.
4.4 正则化的线性回归 Regularized Linear Regression
4.5 正则化的逻辑回归 Regularized Logistic Regression
步骤和前面说的一样，只是在损失函数中加入了规则项。
梯度下降法：
牛顿法：
