luogu P3353 在你窗外闪耀的星星

问题：天空可以理解为一条数轴，在这条数轴上分布着许多颗星星，对于每颗星星都有它的位置Xi和自身的亮度Bi。而窗户所能看到的范围是一个给出的参数W，我们看到的星星也包括窗户边缘的星星。现在，要你求出调整窗户位置后能看到星星的亮度之和最大值。

输入输出格式

输入格式：

一行N,W，分别代表星星的数量和窗户的宽度

余下N行，输入Xi和Bi，代表星星的坐标和亮度

输出格式：

一个数字，代表能看到星星的最大亮度和

输入输出样例

输入样例#1：

6 3
1 2
2 4
3 8
4 4
5 2
1000 1

输出样例#1： 

16

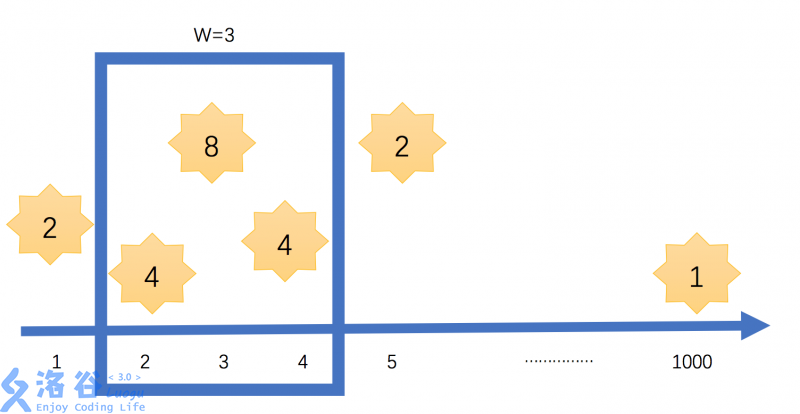
说明：

　　对于10%的数据，W=0（没有边缘）

　　对于40%的数据，W<=1000

　　对于100%的数据，N<=100000，W<=100000，Xi<=100000，1<=Bi<=100

　　除W=0的情况外，W均为>=3的奇数

　　

　在此主要讲线段树做法，若要没接触过的小伙伴建议去了解学习一下:http://www.cnblogs.com/rmy020718/p/8832889.html

思路：
　　明显的线段树板子呗，一段区间最亮，那不就是求一段区间和最大嘛。

#include<cstdio>
#include<iostream>
using namespace std;
int a[100001];
long long n,m,ans,x,y,ch,MAX;
struct ahah{
    long long l,r,sum;
}tree[100001<<2];
void build(int k,int l,int r)    //建树。 
{
    tree[k].l=l;tree[k].r=r;
    if(tree[k].l==tree[k].r)
    {
        tree[k].sum=0;
        return ;
    }
    long long mid=(tree[k].l+tree[k].r)>>1;
    build(k<<1,l,mid);
    build(k<<1|1,mid+1,r);
//    tree[k].sum=tree[k<<1].sum+tree[k<<1|1].sum;  开始不需要修改区间和。 
}
void update(int k)                //此处为单点修改 
{
    if(tree[k].l==tree[k].r)
    {
        tree[k].sum+=y;
        return ;
    }
    long long mid=(tree[k].l+tree[k].r)>>1;
    if(x<=mid)update(k<<1);
    else update(k<<1|1);
    tree[k].sum=tree[k<<1].sum+tree[k<<1|1].sum;
}
void query(int k)            //区间求和。 
{
    if(x<=tree[k].l&&y>=tree[k].r)
    {
        ans+=tree[k].sum;
        return ;
    }
    long long mid=(tree[k].l+tree[k].r)>>1;
    if(x<=mid)query(k<<1);
    if(y>mid)query(k<<1|1);
}
int main()
{
    scanf("%lld%lld",&n,&m);
    build(1,1,100000);        //感觉在后边建树会比较麻烦，就在此建吧，也慢不了多少。 
    for(int i=1;i<=n;i++)
    {
        cin>>x>>y;
        update(1);            //每个亮度依靠单点修改来完成。 
        MAX=max(MAX,x);
    }
    long long u=0;
    for(int i=1;i<=MAX-m+1;i++)        //枚举每段合适区间。 
    {
        ans=0;
        x=i;y=i+m-1;
        query(1);                    //求取区间和 。 
        u=max(u,ans);                // 记录区间最大和。 
    }
    printf("%lld",u);            //输出就好了； 
}

此为个人略解，转载请标明出处：http://www.cnblogs.com/rmy020718/p/8832897.html
　　本人永久联系QQ：2240560936
　　那年你倾尽天下白衣无暇，可曾记得我静月未成一轮春夏，一语落罢，却是了无牵挂。