1.Codeforces Global Round 15 B. Running for Gold

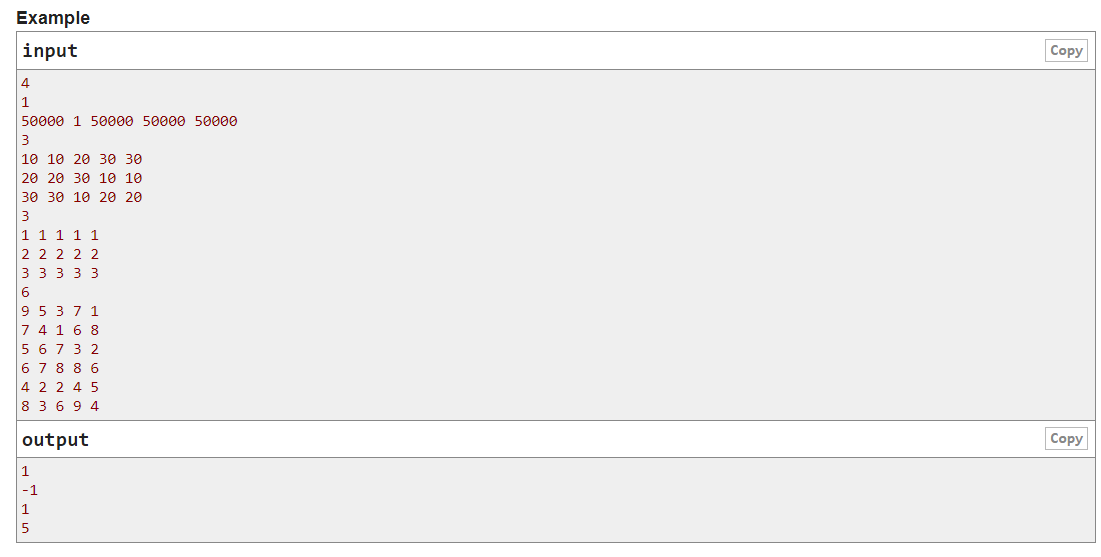
大意:有五项比赛,给出n个运动员在这五项比赛中的排名,运动员A战胜B当且仅当在这五项比赛中至少有三项成绩A在B之上,夺冠必须战胜其他所有人,输出夺冠的运动员,若无人夺冠,输出-1。
题解:设置一个可能夺冠的人w,w从1开始,O(n)枚举2到n每个运动员,若w能战胜 i ,则 i 不可能夺冠;若 i 战胜w,则把w设置为 i ,继续比较。最后得到的 w 是唯一可能夺冠的人,再将w与其他所有运动员比一次,判断w是否能夺冠。

#include<cmath> #include<cstdio> #include<queue> #include<cstdlib> #include<iostream> #include<cstring> #include<algorithm> using namespace std; #define ll long long const int maxn=50000+50; int T,n,a[maxn][6]; bool p[maxn]; template<typename T>void inline read(T &aa){ ll ff=1;char cc=getchar();aa=0; while((cc<'0'||cc>'9')&&cc!='-') cc=getchar(); if(cc=='-') ff=-1,cc=getchar(); while(cc<='9'&&cc>='0') aa=aa*10+cc-48,cc=getchar(); aa*=ff; } bool pd(int x,int y){ int ans=0; for(int i=1;i<=5;i++) if(a[x][i]<a[y][i]) ans++; if(ans>=3 ) return true; return false; } int main(){ cin>>T; while(T--){ memset(p,false,sizeof(p)); cin>>n; for(int i=1;i<=n;i++) for(int j=1;j<=5;j++){ read(a[i][j]); } bool q=0; if(n==1){ cout<<1<<endl; continue; } int w=1; for(int i=2;i<=n;i++){ if(pd(w,i)) continue; else w=i; } for(int i=1;i<=n;i++){ if(i==w) continue; if(!pd(w,i)){ cout<<-1<<endl; q=1; break; } } if(!q) cout<<w<<endl; } return 0; }
2.Codeforces Global Round 15 C. Maximize the Intersections

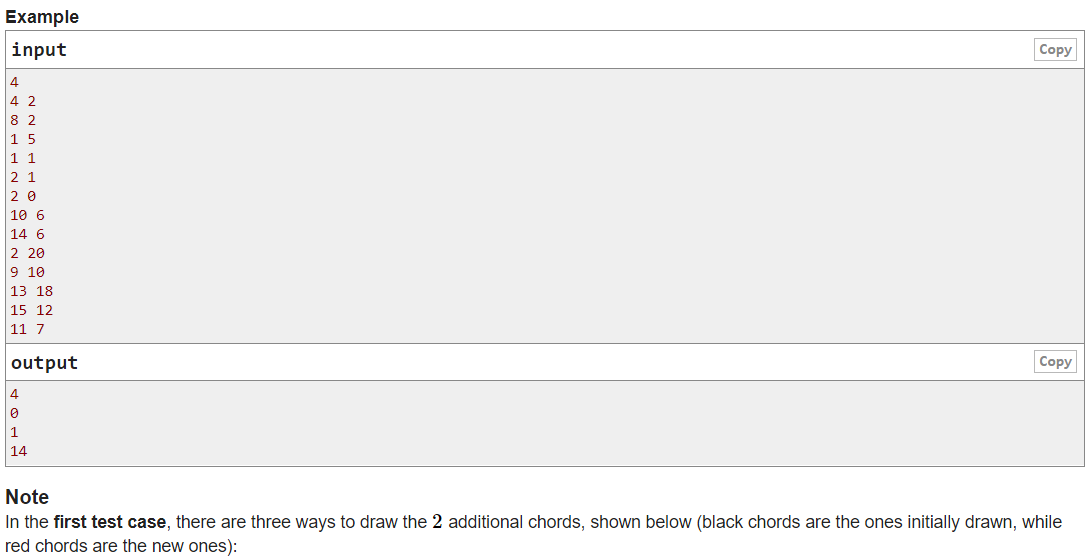

大意:圆上有2n个点,按顺时针方向给出,给出k次操作,每次操作将指定的两个点相连,剩下的点自由相连,使用过的点不能再使用,求最多能有多少交点?
题解:连接1,3,相当于加入一个 [ 1, 3 ] 的区间,对于两个区间,若他们完全包含或者没有公共部分,则这两条弦没有交点。对于剩下的点,下右连上左,下左连上右。

#include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<cstring> #include<algorithm> using namespace std; #define ll long long const int maxn=300; int T,n,k,down[maxn],up[maxn]; bool p[maxn]; struct node{ int l,r; }a[maxn]; bool pd(int x,int y){ if(a[x].l<a[y].l&&a[x].r>a[y].r) return false; if(a[y].l<a[x].l&&a[y].r>a[x].r) return false; if(a[x].r<a[y].l||a[y].r<a[x].l) return false; return true; } template<typename T>void inline read(T &aa){ ll ff=1;char cc=getchar();aa=0; while((cc<'0'||cc>'9')&&cc!='-') cc=getchar(); if(cc=='-') ff=-1,cc=getchar(); while(cc<='9'&&cc>='0') aa=aa*10+cc-48,cc=getchar(); aa*=ff; } int main(){ cin>>T; while(T--){ int ans=0; cin>>n>>k; memset(p,false,sizeof(p)); for(int i=1;i<=k;i++){ int x,y; cin>>x>>y; if(x>y) swap(x,y); p[x]=true;p[y]=true; a[i].l=x;a[i].r=y; if(i>=2){ for(int j=1;j<i;j++){ if(pd(i,j)) ans++; } } } int t=1; for(int i=1;i<=2*n;i++){ if(!p[i]&&t<=n-k){ down[t]=i; t++; } else if(!p[i]&&t>n-k){ up[t-(n-k)]=i; t++; } } t=k; for(int i=1;i<=n-k;i++){ a[++t].l=down[i]; a[t].r=up[i]; for(int j=1;j<t;j++) if(pd(t,j)) ans++; } cout<<ans<<endl; } return 0; }
3.Codeforces Round #685 (Div. 2) E1. Bitwise Queries (Easy Version) E2. Bitwise Queries (Hard Version)
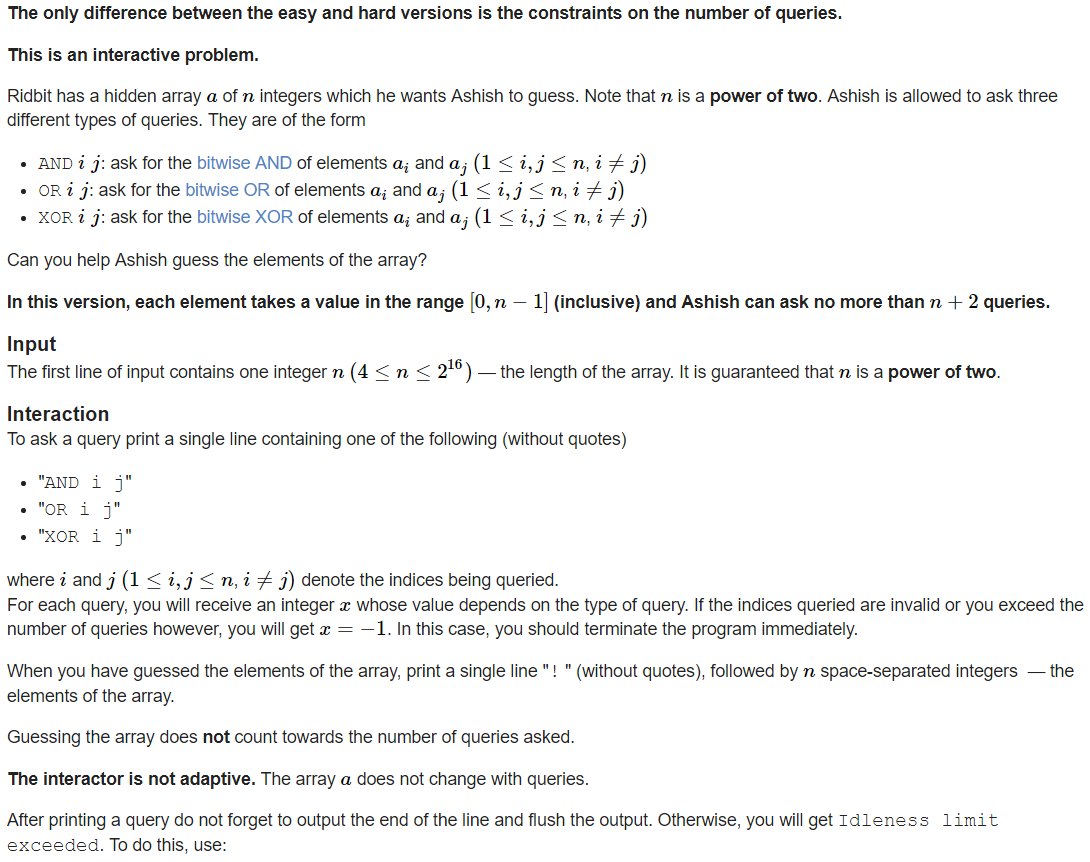

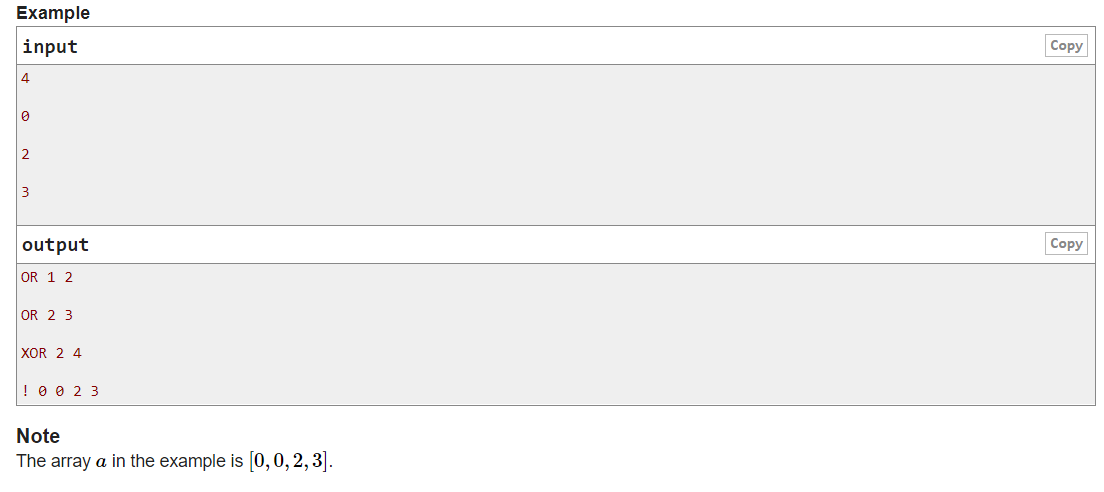
大意:有n个数,n为2的整次幂,每个数都在 [ 0, n-1 ] 之间,你有三种询问方式,你可以得到询问的答案,要求在不超过n+2(n+1)次询问中得到这n个数的值,输出询问方式以及这n个数。
题解:(easy version)首先用n-1次把第一个数与后面n-1个数的异或得到,然后注意,a+b = a ^ b + 2*( a & b ) ,所以再用三次把 a[ 1 ] + a[ 2 ] ,a[ 2 ] + a[ 3 ] , a[ 3 ] + a[ 1 ] 的值得到,就可算出a[ 1 ],从而得到这n个数。
(hard version)这列数有两种情况:第一种是存在两个数相等,第二种是 0~n-1 的全排列。 首先依旧用 n-1 次求出 a[ 1 ]与其他数的异或。对于第一种情况,若有a[ 1 ] ^ a[ j ] == a[ 1 ] ^ a[ k ],则 a[ j ] == a[ k ] 由于 a&a = a,所以我们可以询问 a[ j ] & a[ k ],得到答案后就可以算出 a[ 1 ] 的值,共用n次询问;对于第二种情况,可以找到这样一对,a[ 1 ] ^ a[ k ] == n-1,则 a[ 1 ] & a[ k ] == 0,这样我们就直接找到了一组 a[ 1 ] + a[ k ] == n-1 ,再询问两次 a[ 1 ] & a[ j ],a[ k ] & a[ j ] ,就可以像 easy version 那样求出 a[ 1 ],共 n+1 次询问。
hard version 代码

#include<bits/stdc++.h> using namespace std; #define ll long long const int maxn=100000; int n,a[maxn],w,ans[maxn]; bool p[1000000]; int main(){ cin>>n; bool v=0;int id1,id2; for(int i=2;i<=n;i++){ cout<<"XOR "<<1<<" "<<i<<endl; fflush(stdout); cin>>a[i]; if(!p[a[i]]) p[a[i]]=1; else v=1,id2=i; } if(v){ for(int i=2;i<=n;i++) if(i!=id2&&a[i]==a[id2]){ id1=i; break; } cout<<"AND "<<id1<<" "<<id2<<endl; fflush(stdout); int k; cin>>k; ans[1]=a[id1]^k; } else{ int id1,id2,x,y,z; for(int i=2;i<=n;i++){ if(a[i]==n-1){ id1=i; break; } } x=n-1; if(id1==n) id2=id1-1; else id2=id1+1; cout<<"AND "<<id1<<" "<<id2<<endl;a fflush(stdout); cin>>y;y*=2;y+=(a[id1]^a[id2]); cout<<"AND "<<1<<" "<<id2<<endl; fflush(stdout); cin>>z;z*=2;z+=a[id2]; ans[1]=(x+y+z)/2-y; } for(int i=2;i<=n;i++) ans[i]=(a[i]^ans[1]); cout<<"! "; for(int i=1;i<=n;i++) cout<<ans[i]<<" "; return 0; }
4.Codeforces Round #735 (Div. 2) C. Mikasa
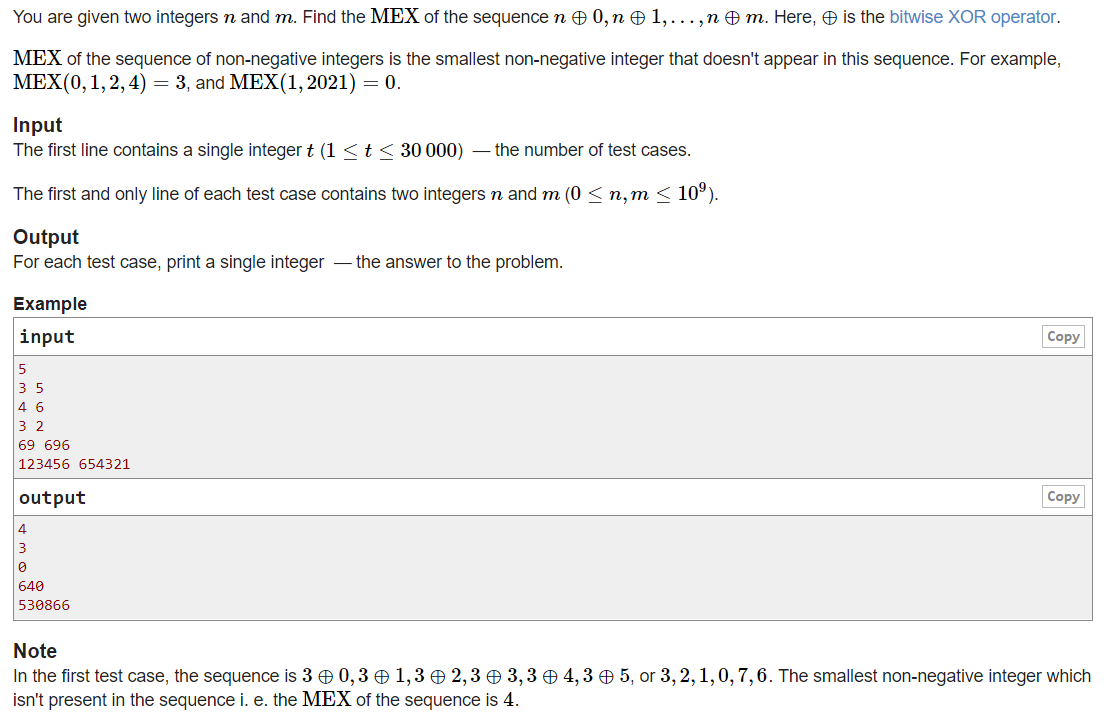
大意:有一列数 n⊕0,n⊕1,……,n⊕m,找出不在这列数中的最小的非负整数。
题解:如果 k 在这列数中,则存在一个 x 满足0 ≤ x ≤ m ,使得 n⊕x=k 。n⊕x=k 等价于 n⊕k=x ,那么问题就可以转化为:求一个最小的 k ,使得 n⊕k ≥ m+1 。那么只需要把m+1和n 的二进制每一位比较贪心选择就可以了。

#include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<cstring> #include<algorithm> using namespace std; #define ll long long const int maxn=105; int T,n,m,a[maxn],b[maxn],ans[maxn]; template<typename T>void inline read(T &aa){ ll ff=1;char cc=getchar();aa=0; while((cc<'0'||cc>'9')&&cc!='-') cc=getchar(); if(cc=='-') ff=-1,cc=getchar(); while(cc<='9'&&cc>='0') aa=aa*10+cc-48,cc=getchar(); aa*=ff; } int main(){ cin>>T; while(T--){ ll Ans=0; cin>>n>>m; if(n>m){ cout<<0<<endl; continue; } int t1=0,t2=0; while(n){ if(n%2==1) a[++t1]=1; else a[++t1]=0; n/=2; } m++; while(m){ if(m%2==1) b[++t2]=1; else b[++t2]=0; m/=2; } for(int i=1;i<=100;i++) ans[i]=0; for(int i=t1+1;i<=t2;i++) a[i]=0; for(int i=1;i<=t2/2;i++) swap(a[i],a[t2-i+1]); for(int i=1;i<=t2/2;i++) swap(b[i],b[t2-i+1]); for(int i=1;i<=t2;i++){ if(a[i]==0&&b[i]==0) ans[i]=0; else if(a[i]==0&&b[i]==1) ans[i]=1; else if(a[i]==1&&b[i]==0){ ans[i]=0; for(int j=i+1;j<=t2;j++) ans[i]=0; break; } else ans[i]=0; } for(int i=1;i<=t2/2;i++) swap(ans[i],ans[t2-i+1]); ll er=1; for(int i=1;i<=t2;i++){ Ans+=1ll*ans[i]*er; er*=2ll; } cout<<Ans<<endl; } return 0; }
5.Codeforces Round #273 (Div. 2) C. Table Decorations
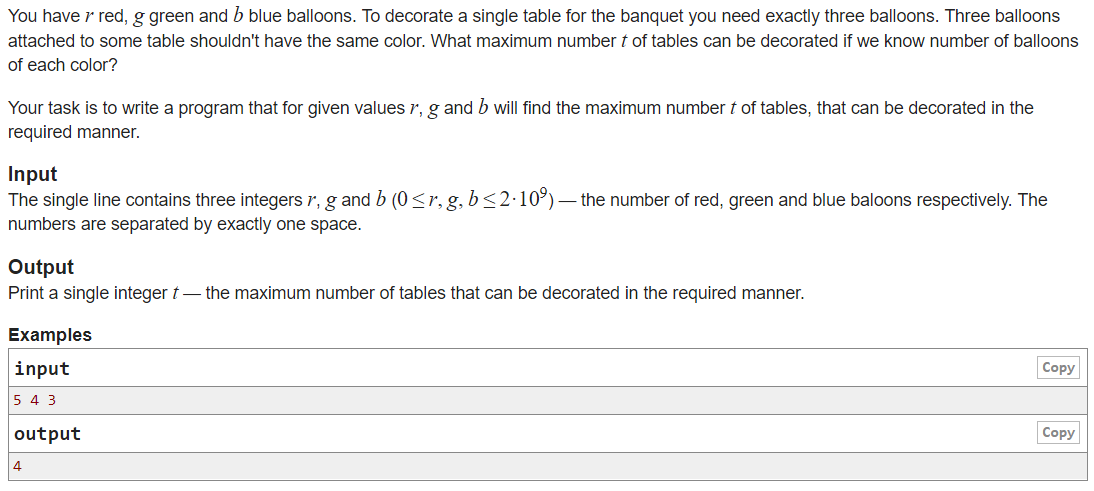
大意:有红绿蓝三种颜色的气球,个数分别为r,g,b,要求每个桌子上放三个气球,且颜色不完全相同,求最多能放多少桌子?
题解:将三种颜色个数排序,a1,a2,a3,若 a1=a2=a3,则答案为a1;若 a2 = a3,则答案为 a1+( a2+a3-2*a1 ) / 3 ;其他情况则是 每次操作最小的和最大的,最小数-1,最大数-2,然后更新。

#include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<cstring> #include<algorithm> using namespace std; #define ll long long ll a[5]; int main(){ ll ans=0; cin>>a[1]>>a[2]>>a[3]; sort(a+1,a+4); if(a[1]==a[3]){ cout<<a[1]<<endl; return 0; } if(a[2]==a[3]){ cout<<a[1]+(a[2]+a[3]-2*a[1])/3; return 0; } ll cha=a[3]-a[2]; ll num=(cha+1)/2; if(a[1]<=num){ a[3]-=a[1]*2; cout<<a[1]+min(a[2],(a[2]+a[3])/3); } else{ ll s=a[1]-num; a[3]-=num*2; if(s%2==0){ a[2]-=s; a[3]-=s; } else{ a[2]-=((s+1)/2)*2; a[3]-=(s/2)*2; } if(a[2]>a[3]) swap(a[2],a[3]); cout<<a[1]+min(a[2],(a[2]+a[3])/3); } return 0; }
6.Codeforces Round #256 (Div. 2) D. Multiplication Table

大意:给出一个n*m的乘法表,其中 a[ i ][ j ] = i*j ,求表中数字从小到大排序后第 k 个为多少?
题解:二分一个x,判断表中严格小于 x 的数有多少个,找到答案大于等于k的第一个数w,则w-1就为所求数。判断方法为:每一行min( ( x - 1 )/ i,m ) 即为这一行严格小于x的数的个数。

#include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<cstring> #include<algorithm> using namespace std; #define ll long long ll n,m,k; bool check(ll x){ ll ans=0; for(int i=1;i<=n;i++) ans+=min((x-1)/i,m); if(ans<k) return true; return false; } int main(){ cin>>n>>m>>k; ll l=1,r=n*m; while(l<=r){ ll mid=l+r>>1; if(check(mid)) l=mid+1; else r=mid-1; } cout<<l-1; return 0; }
7.Codeforces Round #666 (Div. 1) B. Stoned Game

大意:有n堆石子,第 i 堆有 ai 个,T和HL在玩一个游戏,T先手,两人轮流从这n堆石子中的一堆中拿出一个,且不能与上一个人选择相同的堆,最后不能拿的输,输出胜利者。
题解:首先算出这n堆石子总共有sum个,最多的一堆有max个。(1)若max > sum/2,即先手可以一直拿max这一堆,先手必胜;(2)若max <= sum/2。(i)若sum为偶数,后手必胜,证明如下:当sum为0时,显然后手必胜,当sum>=2时,先手拿走一个石子,此时若最多的一堆满足max > sum/2,则转化为(1) 的情况,后手必胜,若不满足max >sum/2,则可继续进行,直到sum=0。(ii)若sum为奇数,先手拿走一个便可转化为(i)的情况,故先手必胜。

#include<cmath> #include<cstdio> #include<cstdlib> #include<iostream> #include<cstring> #include<algorithm> using namespace std; #define ll long long const int maxn=200; int T,n,a[maxn],sum; int main(){ cin>>T; while(T--){ cin>>n; sum=0; for(int i=1;i<=n;i++){ cin>>a[i]; sum+=a[i]; } sort(a+1,a+1+n); if(a[n]>sum/2){ cout<<"T"<<endl; continue; } if(sum%2==0){ cout<<"HL"<<endl; continue; } cout<<"T"<<endl; } return 0; }
8.Codeforces Round #703 (Div. 2) D. Max Median
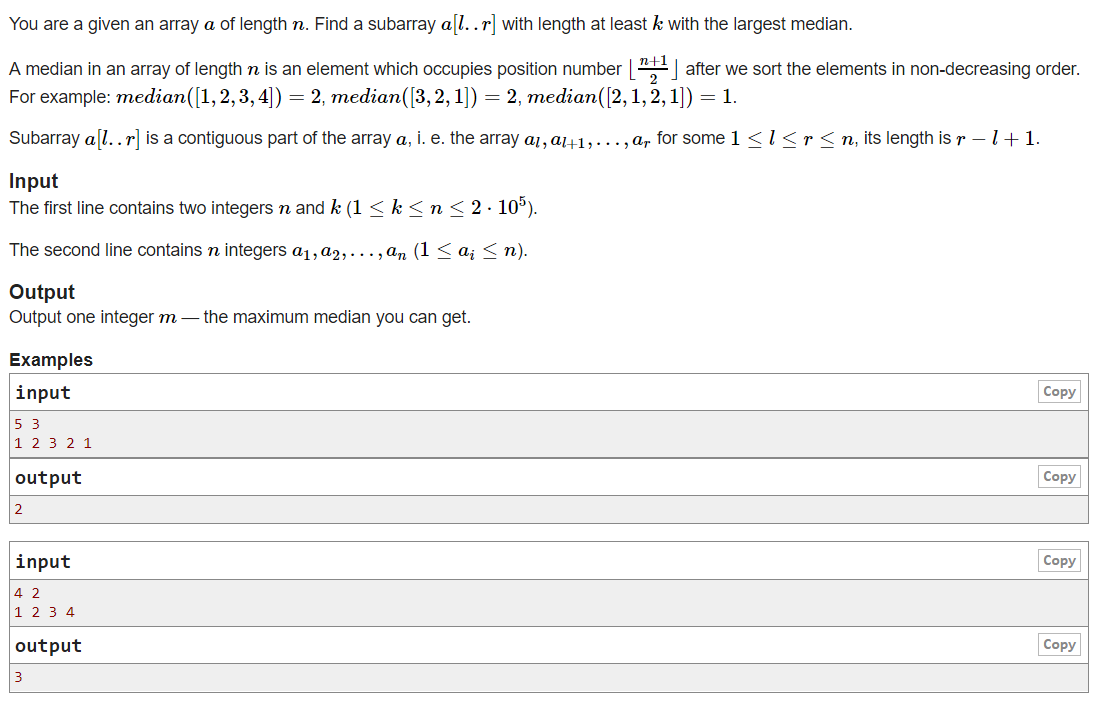
大意:给出 n 个数,找出长度不小于 k 的所有子区间,求这些区间中位数的最大值是多少?
题解:考虑二分答案 x,check的时候把小于 x 的数变为 -1,大于等于 x 的数变为 1。若新数组中有长度不小于 k 的子区间且该区间的和大于 0,则 x 合法。

#include<bits/stdc++.h> using namespace std; #define ll long long const int maxn=2e5+50; int n,k,a[maxn],s[maxn],t,b[maxn],sum[maxn]; bool p[maxn]; bool check(int x){ for(int i=1;i<=n;i++){ if(a[i]<x) b[i]=-1; else b[i]=1; sum[i]=sum[i-1]+b[i]; } int Min=0; if(sum[k]>0) return true; for(int i=k+1,j=1;i<=n;i++,j++){ Min=min(Min,sum[j]); if(sum[i]-Min>0) return true; } return false; } template<typename T>void inline read(T &aa){ ll ff=1;char cc=getchar();aa=0; while((cc<'0'||cc>'9')&&cc!='-') cc=getchar(); if(cc=='-') ff=-1,cc=getchar(); while(cc<='9'&&cc>='0') aa=aa*10+cc-48,cc=getchar(); aa*=ff; } int main(){ cin>>n>>k; for(int i=1;i<=n;i++){ read(a[i]); if(!p[a[i]]) s[++t]=a[i],p[a[i]]=1; } sort(s+1,s+1+t); int l=1,r=t; while(l<=r){ int m=l+r>>1; if(check(s[m])) l=m+1; else r=m-1; } cout<<s[l-1]; return 0; }
9.Codeforces Round #715 (Div. 1) A. Binary Literature

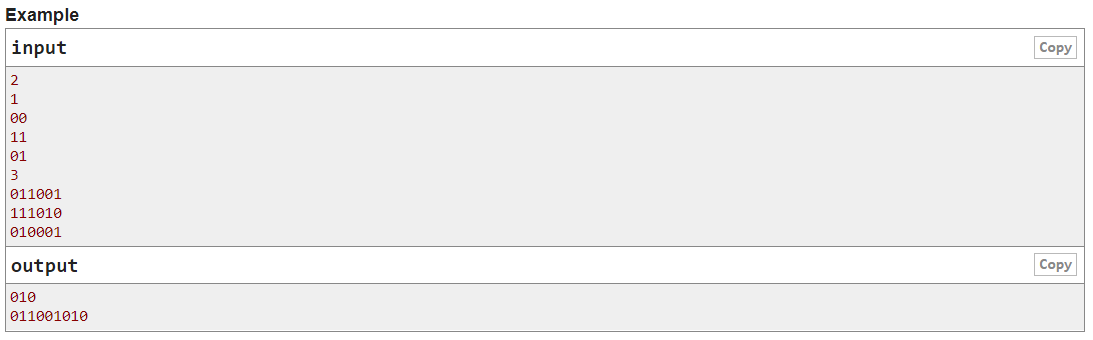
大意:给出3个长度为2n的01串,要求构造一个长度最多为3n的01串,使得这3个01串中至少有2个是该串的子序列。
题解:考虑两个串s和t,可以想到一种构造方案长度为4n-lcs(s,t),那么,只需找到这3个串中 lcs 大于等于n的2个串就行。由于是01串,所以对于每个串必然有0的个数大于n或者1的个数大于n,那么必然存在两个串,他们的公共子序列长度达到n。

#include<bits/stdc++.h> using namespace std; #define ll long long const int maxn=2e5+50; int T,n; char a[maxn],b[maxn],c[maxn]; string ans; void work(char *aa,char *bb,int o){ char op=o+'0',oop; if(op=='1') oop='0'; else oop='1'; int l1=1,l2=1; while(1){ if(l1<=2*n&&l2<=2*n){ if(aa[l1]==bb[l2]){ ans+=aa[l1]; l1++; l2++; continue; } if(aa[l1]==op){ ans+=oop; l2++; continue; } if(bb[l2]==op){ ans+=oop; l1++; continue; } } if(l1>2*n&&l2>2*n) return ; if(l1>2*n){ ans+=bb[l2]; l2++; } else{ ans+=aa[l1]; l1++; } } } template<typename T>void inline read(T &aa){ ll ff=1;char cc=getchar();aa=0; while((cc<'0'||cc>'9')&&cc!='-') cc=getchar(); if(cc=='-') ff=-1,cc=getchar(); while(cc<='9'&&cc>='0') aa=aa*10+cc-48,cc=getchar(); aa*=ff; } int main(){ cin>>T; while(T--){ cin>>n; ans.clear(); cin>>a+1; cin>>b+1; cin>>c+1; int fa=0,fb=0,fc=0,x=0,y=0; for(int i=1;i<=2*n;i++) if(a[i]=='0') x++; else y++; if(x>y) fa=0; else fa=1; x=0;y=0; for(int i=1;i<=2*n;i++) if(b[i]=='0') x++; else y++; if(x>y) fb=0; else fb=1; x=0;y=0; for(int i=1;i<=2*n;i++) if(c[i]=='0') x++; else y++; if(x>y) fc=0; else fc=1; if(fa==fb){ work(a,b,fa); cout<<ans<<endl; } else if(fa==fc){ work(a,c,fa); cout<<ans<<endl; } else{ work(b,c,fb); cout<<ans<<endl; } } return 0; }
