自然归并排序算法时间复杂度分析

最近在看一部美剧《breaking bad》，从中领会了不少东西。回头再看过去写的博客，感觉真是很糟糕。真正自己的东西极少，大多数内容都是网上一搜一大堆的玩意，那么，这样的博客写着有什么意思呢？

从今往后，我的博客一定要写进自己的思想，就算没有创新，也一定要有独立思考求解的过程。

这篇对自然归并排序算法时间复杂度的分析便是第一篇。

对于普通归并排序算法，我就不赘述了。任何一本算法书籍都有介绍，随便用python写了一笔：

class Merge():
    def __init__(self):
        self.tmp_arr = [0,0,0,0,0,0,0,0,0,0,0,0]

    def merge(self, arr, start, mid, end):
        for i in range(start, end+1):
            self.tmp_arr[i] = arr[i]
        j = mid + 1
        k = start
        for i in range(start, end+1):
            if k > mid:
                arr[i] = self.tmp_arr[j]
                j += 1
            elif j > end:
                arr[i] = self.tmp_arr[k]
                k += 1
            elif self.tmp_arr[j] < self.tmp_arr[k]:
                arr[i] = self.tmp_arr[j]
                j += 1
            else:
                arr[i] = self.tmp_arr[k]
                k += 1
    def sort(self, arr, start, end):
        if end <= start:
            return 
        mid = start + (end - start) / 2
        self.sort(arr, start, mid)
        self.sort(arr, mid + 1, end)
        self.merge(arr, start, mid ,end)
        
mobj = Merge()
arr = [5,3,4,7,1,9,0,4,2,6,8]
mobj.sort(arr, 0, len(arr)-1)
for i in range(len(arr)):
    print arr[i]

其时间复杂度为O(nlogn)，归并排序的比较是分层次来归并的（第一次是两两归并，之后再在第一次归并的基础上两两归并，每一层归并的次数为上一层除二，最终形成一二叉树，该二叉树的高即为归并次数logn。而每一层的比较次数恒等于n，所以时间复杂度求得nlogn）。

自然归并排序算法是在归并排序算法基础上的改进，首先将数列中，已经有序的数分为小组，再在这些小组的基础上归并。

例如 5,3,4,7,1,9,0,4,2,6,8

则可首先得到{5},{3},{4,7},{1,9},{0,4},{2,6,8}

第一次归并得到{3,5},{1,4,7,9},{0,2,4,6,8}

第二次归并得到{1,3,4,5,7,9},{0,2,4,6,8}

可以看出，原理同样是二路归并，只不过最开始现将有序的部分划分了下。所以那一次‘划分了’多少个组，将决定以后的归并是否更顺利（树的层数更少）

普通归并排序的情况，第一次归并得到的组数为g = N/2

自然归并排序的情况，设第一次归并得到的组数为g，因为，一个数为一组的概率为1/2，两个数为一组的概率为1/4,n个数为一组的概率为2的n次方分之一。则可求得等式：

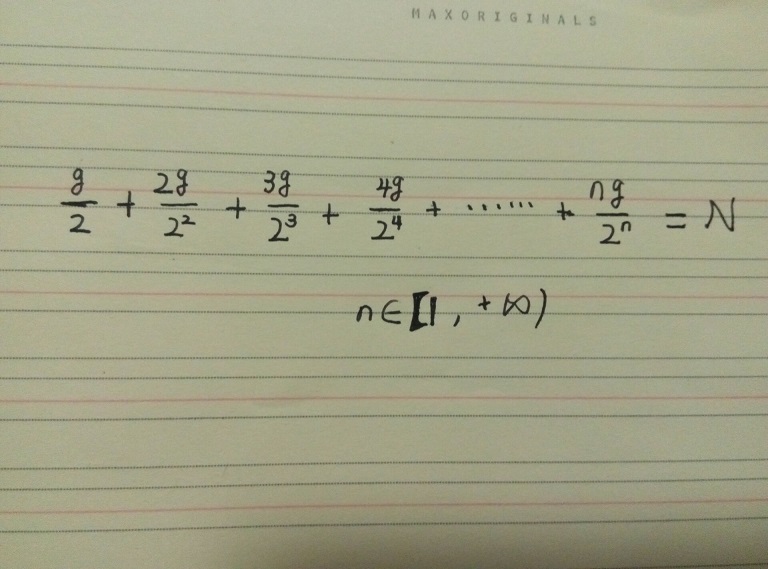
继续推导：

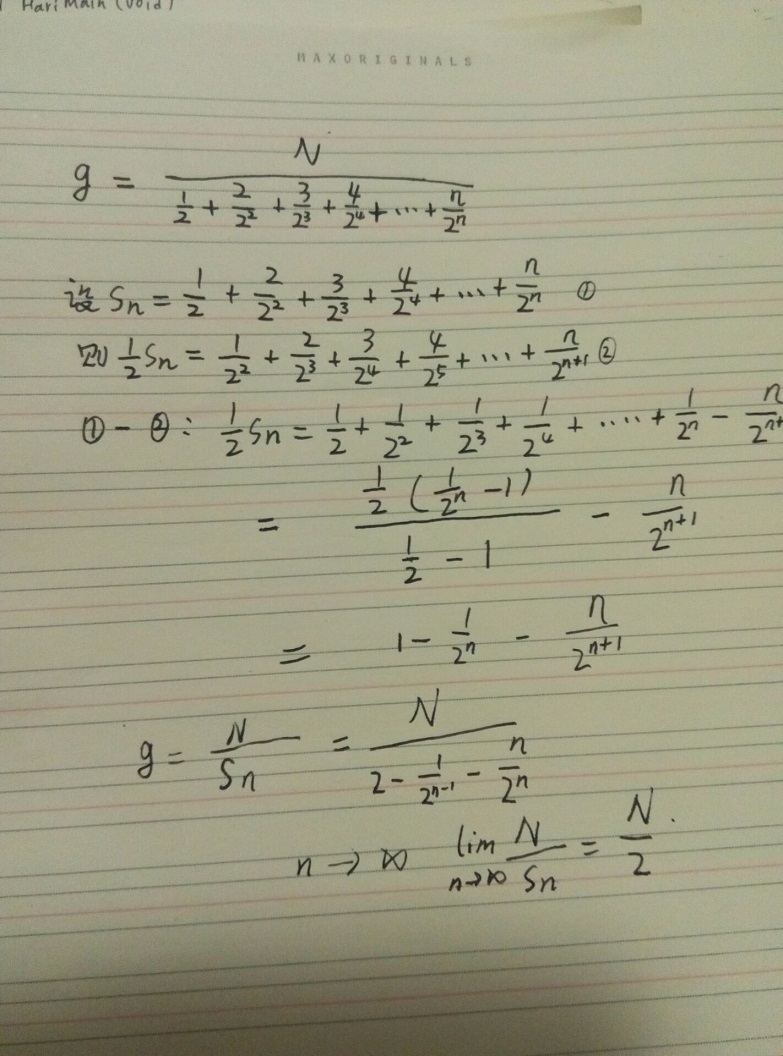
可知，在随机情况下，自然归并排序分的组数是与普通归并排序 无限趋近相等的。

结论：在分组数相等的基础上，继续进行二路归并，之后的‘二叉树’的高度便是一样的。所以时间复杂度同样为O(nlogn)。

         然而，若已知待排序数列相对有序的情况，则自然归并排序算法是优于普通归并排序算法的。