Problem Description
JGShining's kingdom consists of 2n(n is no more than 500,000) small cities which are located in two parallel lines.
Half of these cities are rich in resource (we call them rich cities) while the others are short of resource (we call them poor cities). Each poor city is short of exactly one kind of resource and also each rich city is rich in exactly one kind of resource. You may assume no two poor cities are short of one same kind of resource and no two rich cities are rich in one same kind of resource.
With the development of industry, poor cities wanna import resource from rich ones. The roads existed are so small that they're unable to ensure the heavy trucks, so new roads should be built. The poor cities strongly BS each other, so are the rich ones. Poor cities don't wanna build a road with other poor ones, and rich ones also can't abide sharing an end of road with other rich ones. Because of economic benefit, any rich city will be willing to export resource to any poor one.
Rich citis marked from 1 to n are located in Line I and poor ones marked from 1 to n are located in Line II.
The location of Rich City 1 is on the left of all other cities, Rich City 2 is on the left of all other cities excluding Rich City 1, Rich City 3 is on the right of Rich City 1 and Rich City 2 but on the left of all other cities ... And so as the poor ones.
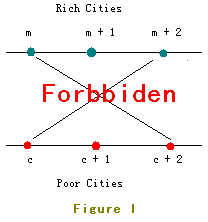
But as you know, two crossed roads may cause a lot of traffic accident so JGShining has established a law to forbid constructing crossed roads.
For example, the roads in Figure I are forbidden.
In order to build as many roads as possible, the young and handsome king of the kingdom - JGShining needs your help, please help him. ^_^
Half of these cities are rich in resource (we call them rich cities) while the others are short of resource (we call them poor cities). Each poor city is short of exactly one kind of resource and also each rich city is rich in exactly one kind of resource. You may assume no two poor cities are short of one same kind of resource and no two rich cities are rich in one same kind of resource.
With the development of industry, poor cities wanna import resource from rich ones. The roads existed are so small that they're unable to ensure the heavy trucks, so new roads should be built. The poor cities strongly BS each other, so are the rich ones. Poor cities don't wanna build a road with other poor ones, and rich ones also can't abide sharing an end of road with other rich ones. Because of economic benefit, any rich city will be willing to export resource to any poor one.
Rich citis marked from 1 to n are located in Line I and poor ones marked from 1 to n are located in Line II.
The location of Rich City 1 is on the left of all other cities, Rich City 2 is on the left of all other cities excluding Rich City 1, Rich City 3 is on the right of Rich City 1 and Rich City 2 but on the left of all other cities ... And so as the poor ones.
But as you know, two crossed roads may cause a lot of traffic accident so JGShining has established a law to forbid constructing crossed roads.
For example, the roads in Figure I are forbidden.

In order to build as many roads as possible, the young and handsome king of the kingdom - JGShining needs your help, please help him. ^_^
Input
Each test case will begin with a line containing an integer n(1 ≤ n ≤ 500,000). Then n lines follow. Each line contains two integers p and r which represents that Poor City p needs to import resources from Rich City r. Process to the end of file.
Output
For each test case, output the result in the form of sample.
You should tell JGShining what's the maximal number of road(s) can be built.
You should tell JGShining what's the maximal number of road(s) can be built.
Sample Input
2
1 2
2 1
3
1 2
2 3
3 1
Sample Output
Case 1:
My king, at most 1 road can be built.
Case 2:
My king, at most 2 roads can be built.
Hint
Huge input, scanf is recommended.
题意:富人路与穷人路都分别有从1到n的n个点,现在要在富人点与穷人点之间修路,但是要求路不能交叉,问最多能修多少条。
思路:首先这道题已经规定了每个点都是按顺序排列好的,所以要求路不能交叉,那么每下一个点都必须必前一个点要大,而这个特点,很明显就是LIS,但是要注意的是,这里将有500000个输入,在我昨天POJ的2533题我就发过了n^2与nlogn的LIS解法,而这里为了不超时,就必须用到后者
#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
int a[500005],dp[500005],c[500005],n;
int bin(int size,int k)
{
int l = 1,r = size;
while(l<=r)
{
int mid = (l+r)/2;
if(k>c[mid] && k<=c[mid+1])
return mid+1;
else if(k<c[mid])
r = mid-1;
else
l = mid+1;
}
}
int LIS()
{
int i,j,ans=1;
c[1] = a[1];
dp[1] = 1;
for(i = 2;i<=n;i++)
{
if(a[i]<c[1])
j = 1;
else if(a[i]>c[ans])
j = ++ans;
else
j = bin(ans,a[i]);
c[j] = a[i];
dp[i] = j;
}
return ans;
}
int main()
{
int i,x,y,ans,cas = 1;
while(~scanf("%d",&n))
{
for(i = 1; i<=n; i++)
{
scanf("%d%d",&x,&y);
a[x] = y;
}
ans = LIS();
printf("Case %d:
",cas++);
if(ans-1)
printf("My king, at most %d roads can be built.
",ans);
else
printf("My king, at most %d road can be built.
",ans);
printf("
");
}
return 0;
}