转载请注明出处:点我
昨天参加了企鹅的2015年实习生招聘的笔试,编程题第一道题就是约瑟夫圆环问题,要求用C++来实现。
约瑟夫圆环问题其实是一个很有名的问题:问题的描述为:
设有编号为1,2,……,n的n(n>0)个人围成一个圈,从第k个人开始报数,报到m时停止报数,报m的人出圈,再从他的下一个人起重新报数,报到m时停止报数,报m的出圈,……,如此下去,直到所有人全部出圈为止。当任意给定n和m后,设计算法求n个人出圈的次序。
这个问题网上的解法很多,我的思路是这样的:
所有人排成一排,每次由站在(最左边)排头的人报数(如果不是由站在排头的人报数,比如由站在第n位的人报数,则把前面n-1个人按照次序放到队伍的最后面),如果站在排头的人不符合出圈的要求,就把排头的人出队列,并站到排尾,队列全部往前移动一个位置。再由排头的人报数,以此类推。
这里以7个人为例,从第3个人开始报数,报到3的出队列,下一个接着报,以count表示当前的报数:
以7个人为例,每个人的编号依次为1,2,...7,把7个人依次放在一个队列里面,如下图所示:

因为是从第三个人开始报数,所以要把第三个人前面的两个人按照先后次序放到排尾,结果如下图所示:

此时,序号为3的人位于排头,由他开始报数,报数count = 1,不符合出队列要求,所以把他出队列,牌都排尾,然后队伍整体向前移动一个位置,如下图所示:

此时由位于排头的序号为4的人进行报数,count = 2,也不符合要求,同样的出队列,放到排尾,

此时序号为5的人站在排头,报数count=3,符合要求,现在把序号为5的人出队列,并输出序号
此时第一轮报数完成,序号为5的人出队列,输出5,设置count=0,并开始下一轮报数

现在序号6位于排头,报数count=1,不符合要求,出队列,站在排尾
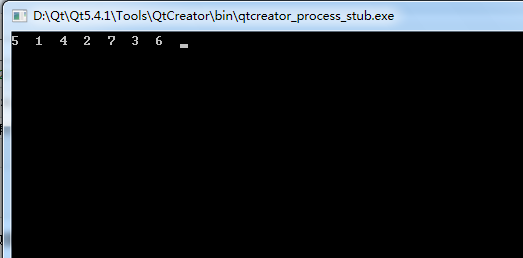
重复上面的过程,即可得到出队列的次序为:
5 1 4 2 6 3 7
下面是代码实现:
1 /* 2 * number个人围城一圈,从第start个人开始报数, 3 * 报到第k个数的人圈,下一个接着从头开始报数 4 * author:rio_2607 5 */ 6 void yuesefu(int number,int start,int k) 7 { 8 deque<int> queue; 9 //把number个人依次放入一个deque队列中去 10 for(int i = 1;i <= number;++i) 11 queue.push_back(i); 12 int count = 1; 13 while(count < start) 14 { 15 //只要还没有达到第start个人,就依次把最前面的元素放到最后面去 16 queue.push_back(queue.front()); 17 queue.pop_front(); 18 ++count; 19 } 20 while(queue.size() != 0) 21 { 22 int step = 1; 23 while(step < k) 24 { 25 //只要还没有报数报到第k个就把当前的元素放到queue的最后面去 26 queue.push_back(queue.front()); 27 queue.pop_front(); 28 ++step; 29 } 30 31 //数到了第k个,把第k个删除 32 cout << queue.front() << " "; 33 queue.pop_front(); 34 } 35 }
因为要频繁的在队列的头部和尾部插入数据,删除数据,所以选择用STL中的deque容器来实现。
下面是测试程序:7个人,从第三个人开始报数,报道3的人出队列:
1 int main() 2 { 3 int start = 3,step = 3; 4 int number = 7; 5 yuesefu(number,start,step); 6 return 0; 7 }
得到的输出结果是: