二叉树的相关概念
树高度,节点层数,节点度数,路径,叶节点,分支节点,根节点,父节点,左节点,右节点,兄弟节点,祖先节点,子孙节点,左子树,右子树
①结点:包含一个数据元素及若干指向子树分支的信息
②结点的度:一个结点拥有子树的数目称为结点的度
③叶子结点:也称为终端结点,没有子树的结点或者度为零的结点
④分支结点:也称为非终端结点,度不为零的结点称为非终端结点
⑤树的度:树中所有结点的度的最大值
⑥结点的层次:从根结点开始,假设根结点为第1层,根结点的子节点为第2层,依此类推,如果某一个结点位于第L层,则其子节点位于第L+1层
⑦树的深度:也称为树的高度,树中所有结点的层次最大值称为树的深度
⑧有序树:如果树中各棵子树的次序是有先后次序,则称该树为有序树
⑨无序树:如果树中各棵子树的次序没有先后次序,则称该树为无序树
⑩森林:由m(m≥0)棵互不相交的树构成一片森林。如果把一棵非空的树的根结点删除,则该树就变成了一片森林,森林中的树由原来根结点的各棵子树构成

二叉树的应用场景
- 普通的二叉树,很难构成现实的应用场景,但因其简单,常用于学习研究,平衡二叉树则是实际应用比较多的。常见于快速匹配、搜索等方面。
- 常用的树有:AVL树、红黑树、B+树、Trie(字典)树。
1、AVL树: 最早的平衡二叉树之一。应用相对其他数据结构比较少。windows对进程地址空间的管理用到了AVL树。
2、红黑树: 平衡二叉树,广泛用在C++的STL中。如map和set都是用红黑树实现的。还有Linux文件管理。
3、B/B+树: 用在磁盘文件组织 数据索引和数据库索引。
4、Trie树(字典树): 用在统计和排序大量字符串,如自动机、M数据库索引。
二叉树的构建
P:前/中/后序是指根被读取的顺序
节点顺序都是先左后右
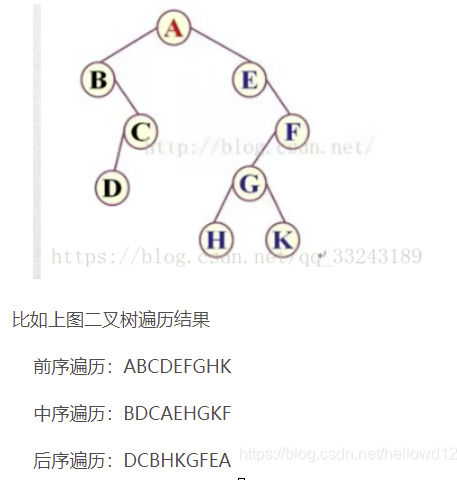

二叉树重建
- 二叉树的重建,只能在提供前序+中序,或者后序+中序的情况下,才可以正常的重构。
https://blog.csdn.net/hellowd123/article/details/99692395