一、模型描述
符号表示:


(i)表示第i个样本,在矩阵中可以表示为第几行第几列

h(hypothesis)——假设函数
二、代价函数(cost function)
线性回归的目标函数

拟合函数(fit data)—— 确定函数的参数θ0,θ1
减少(最小化)假设的输出值(预测值)和真实值之间差的平方和
因此定义代价函数:

平方误差函数(回归问题常用函数)

goal--optimization objective
目标找代价函数的最小值
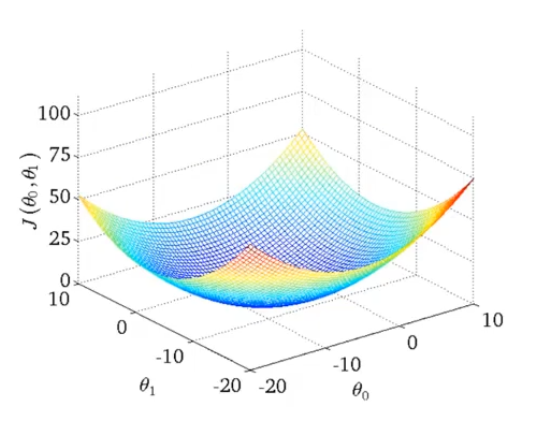
3D,两个参数的代价函数
等高线图(更方便的形式显示代价函数)

同一个圆上的代价函数值相同
三、梯度下降
gradient descend(最小化代价函数)

初始化θ0,θ1的值
不同的初始化值可能会得到不同的局部最优处,因此需要更新

:=表示赋值(eg.a:=a+1)
=表示判断(eg:a=b,a是否等于b
α 表示学习率,控制梯度下降时迈出多大的步子,α 值大则幅度大
需要同时更新θ0,θ1
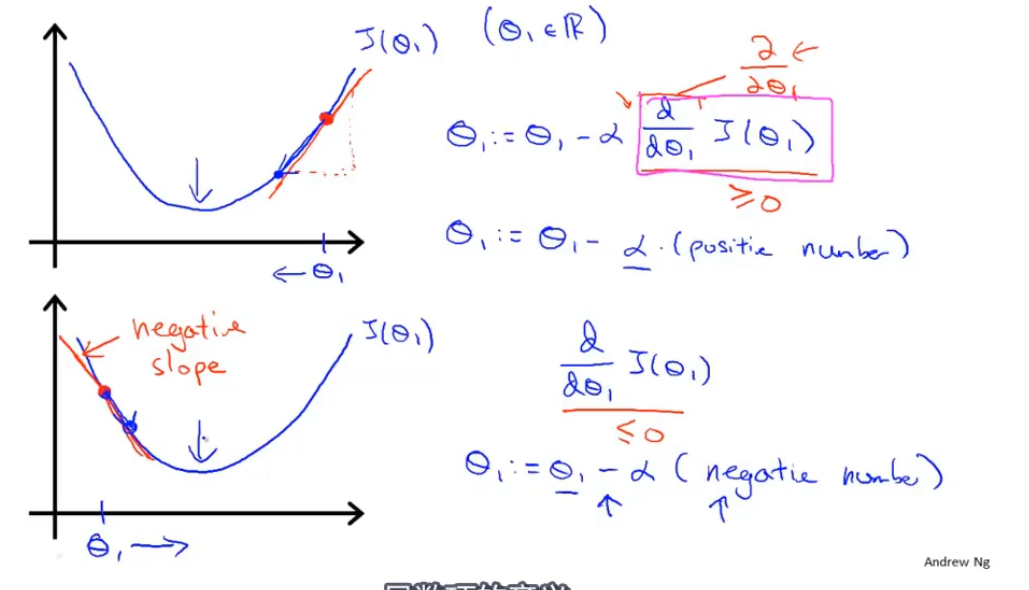
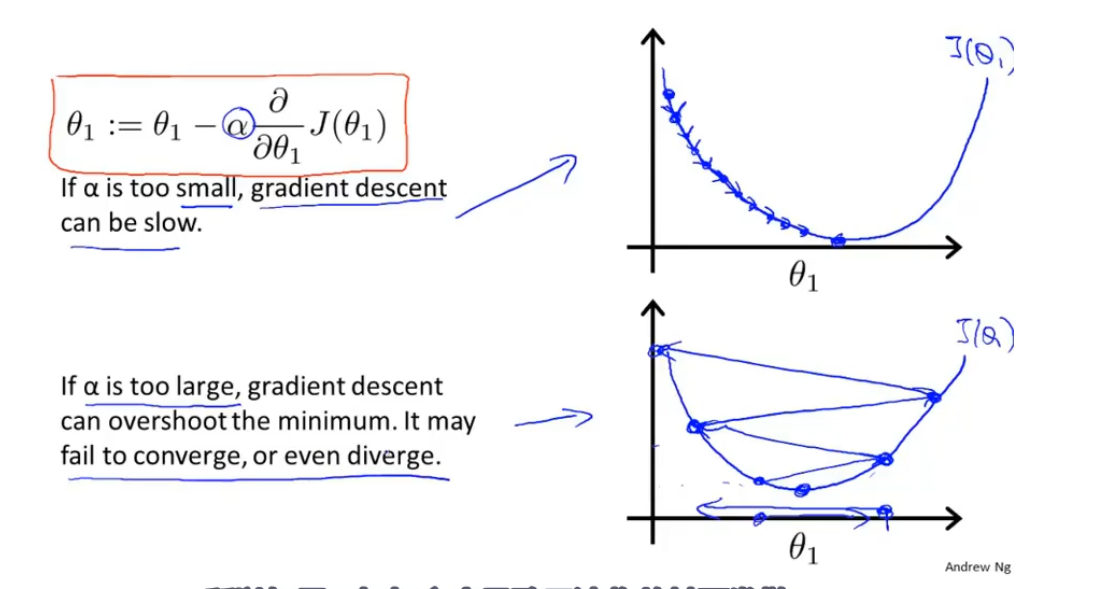
如果学习率过大可能会越过最优点,导致无法收敛
当到了参数不会再更新时,就是最优点(例如局部导数为0的点)
注意当越来越接近最优点的时候,局部导数值会越来越小,因此没有必要改变α 的值
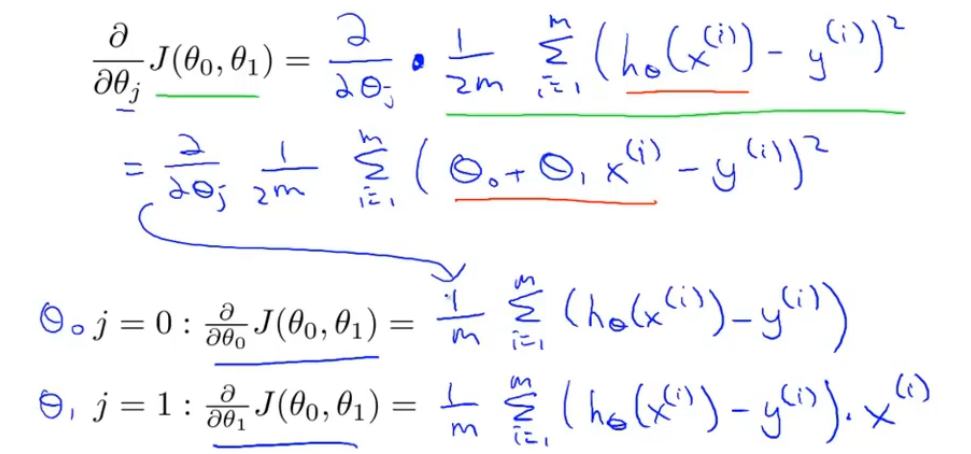
凸函数(弓形函数)

P:局部最优解的集合
这里仅有一个全局最优解,没有局部最优解
因此使用线性回归,都会收敛到最优解
更适用于大数据
Batch梯度下降——每一步梯度下降都遍历了整个训练集的样本