<3>2-D边界碰撞检测
一、使用向量进行障碍检测的原理
在游戏中进行障碍碰撞检测,基本思路是这样的:给定一个障碍范围,判断物体在这次移动后会不会进入这个范围,如果会,就发生碰撞,否则不发生碰撞。在实际操作中,是用物体的边界来判断还是其他部位判断完全取决于编程者。这时候,就可以从这个部位沿着速度的方向引出一条速度向量线,判断一下这条线段(从检测部位到速度向量终点)和障碍边界线有没有交点,如果有,这个交点就是碰撞点。
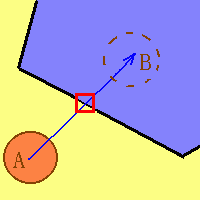
上面物体A,在通过速度向量移动之后将到达B位置。但是,这次移动将不会顺利进行,因为我们发现,碰撞发生了。碰撞点就在那个红色区域中,也就是速度向量和边界线的交点。 我们接下来的工作就是要计算这个交点,这是一个解线性方程组的过程,那么我们将要用到一样工具...
二、一个解线性方程组的有力工具---克兰姆(Cramer)法则
首先要说明一下的是,这个法则是有局限性的,它必须在一个线性方程组的系数行列式非零的时候才能够使用。别紧张,我会好好谈谈它们的。首先让我来叙述一下这个法则(我会试着让你感觉到这不是一堂数学课):
如果线性方程组:
A11*X1 + A12*X2 + ... + A1n*Xn = b1
A21*X1 + A22*X2 + ... + A2n*Xn = b2
...................................
An1*X1 + An2*X2 + ... + Ann*Xn = bn
的系数矩阵 A =
__ __
| A11 A12 ... A1n |
| A21 A22 ... A2n |
| ....................... |
| An1 An2 ... Ann |
-- --
的行列式 |A| != 0
线性方程组有解,且解是唯一的,并且解可以表示为:
X1 = d1/d , X2 = d2/d , ... , Xn = dn/d (这就是/A/=d为什么不能为零的原因)
这里d就是行列式/A/的值,dn(n=1,2,3...)是用线性方程组的常数项b1,b2,...,bn替换系数矩阵中的第n列的值得到的矩阵的行列式的值,即:
| b1 A12 ... A1n |
d1 = | b2 A22 ... A2n |
| ..................... |
| bn An2 ... Ann |
| A11 b1 ... A1n |
d2 = | A21 b2 ... A2n |
| ..................... |
| An1 bn ... Ann |
...
| A11 A12 ... b1 |
dn = | A21 A22 ... b2 |
| ..................... |
| An1 An2 ... bn |
别去点击关闭窗口按钮!我现在就举个例子,由于我们现在暂时只讨论2-D游戏(3-D以后会循序渐进的谈到),就来个2-D线性方程组:
(1) 4.0*X1 + 2.0*X2 = 5.0
(2) 3.0*X1 + 3.0*X2 = 6.0
这里有两个方程,两个未知量,则根据上面的Cramer法则:
| 4.0 2.0 |
d = | 3.0 3.0 | = 4.0*3.0 - 2.0*3.0 = 6.0 (2阶行列式的解法,'/'对角线相乘减去'/'对角线相乘)
| 5.0 2.0 |
d1 = | 6.0 3.0 | = 5.0*3.0 - 2.0*6.0 = 3.0
| 4.0 5.0 |
d2 = | 3.0 6.0 | = 4.0*6.0 - 5.0*3.0 = 9.0
则
X1 = d1/d = 3.0/6.0 = 0.5
X2 = d2/d = 9.0/6.0 = 1.5
好了,现在就得到了方程组的唯一一组解。
是不是已经掌握了用Cramer法则解2-D线性方程组了?如果是的话,我们继续。
三、深入研究
这里的2-D障碍碰撞检测的实质就是判断两条线段是否有交点,注意不是直线,是线段,两直线有交点不一定直线上的线段也有交点。现在我们从向量的角度,写出两条线段的方程。
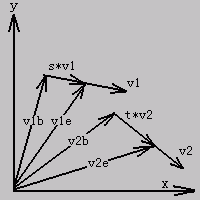
现在有v1和v2两条线段,则根据向量加法:
v1e = v1b + s*v1
v2e = v2b + t*v2
v1b和v2b分别是两线段的一端。s,t是两个参数,它们的范围是[0.0,1.0],当s,t=0.0时,v1e=v1b,v2e=v2b;当s,t=1.0时,v1e和v2e分别是两线段的另一端。s,t取遍[0.0,1.0]则v1e和v2e取遍两线段的每一点。
那么我们要判断v1和v2有没有交点,就让v1e=v2e,看解出的s,t是不是在范围内就可以了:
v1e = v2e
=> v1b + s*v1 = v2b + t*v2
=> s*v1 - t*v2 = v2b - v1b
写成分量形式:
s*x_v1 - t*x_v2 = x_v2b - x_v1b
s*y_v1 - t*y_v2 = y_v2b - y_v1b
现在是两个方程式,两个未知数,则根据Cramer法则:
| x_v1 -x_v2 | | 4.0 -2.0 |
d = | y_v1 -y_v2 | = | 1.0 -3.0 | = -10.0
| x_v2b-x_v1b -x_v2 | | 5.0 -2.0 |
d1 = | y_v2b-y_v1b -y_v2 | = | 2.0 -3.0 | = -11.0
s = d1/d = -11.0/-10.0 = 1.1 > 1.0
现在s已经计算出来,没有在[0.0,1.0]内,所以两线段没有交点,从图上看很直观。t没有必要再计算了。所以是物体与障碍没有发生碰撞。如果计算出的s,t都在[0.0,1.0]内,则把它们带入原方程组,计算出v1e或者v2e,它的分量就是碰撞点的分量。
四、理论上的东西已经够多的了,开始写程序
我现在要写一个用于处理障碍碰撞检测的函数,为了测试它,我还准备安排一些障碍:
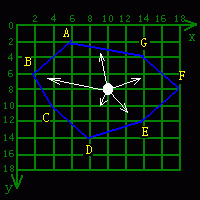
这是一个凸多边形,我让一个质点在初始位置(10,8),然后给它一个随机速度,这个随机速度的两个分速度在区间[1.0,4.0]内,同时检测是否与边界发生碰撞。当碰撞发生时,就让它回到初始位置,重新给一个随机速度。
// 首先我要记下凸多边形的边界坐标 float poly[2][8] = { { 6.0f , 2.0f , 4.0f , 8.0f , 14.0f , 18.0f , 14.0f , 6.0f } , // 所有点的x分量,最后一个点和第一个点重合 { 2.0f , 6.0f , 10.0f , 14.0f , 12.0f , 8.0f , 4.0f , 2.0f } // 所有点的y分量 } ; // 定义一些变量 float x , y ; // 这是质点的位置变量 float vx , vy ; // 质点的速度向量分量 // 好,开始编写碰撞检测函数 bool CollisionTest() { // 当发生碰撞时返回true,否则返回false float s , t ; // 线段方程的两个参数 // 各个参量 float x_v1 , x_v2 , y_v1 , y_v2 ; float x_v2b , x_v1b , y_v2b , y_v1b ; for( int i = 0 ; i < 8-1 ; ++i ) { // 循环到倒数第二个点
// 障碍线段 x_v1 = poly[0][i+1]-poly[0][i] ; y_v1 = poly[1][i+1]-poly[1][i] ; // 物体速度向量 x_v2 = vx ; y_v2 = vy ; // 障碍向量初始点 x_v1b = poly[0][i] ; y_v1b = poly[1][i] ; // 物体位置 x_v2b = x ; y_v2b = y ; // 计算d,d1和d2 // | x_v1 -x_v2 | //d = | y_v1 -y_v2 | // | x_v2b-x_v1b -x_v2 | //d1 = | y_v2b-y_v1b -y_v2 | // | x_v1 x_v2b-x_v1b | //d2 = | y_v1 y_v2b-y_v1b | d = (x_v1*(-y_v2))-((-x_v2)*y_v1) ; d1 = ((x_v2b-x_v1b)*(-y_v2))-((-x_v2)*(y_v2b-y_v1b)) ; d2 = (x_v1*(y_v2b-y_v1b))-((x_v2b-x_v1b)*y_v1) ; // 判断d是否为零 if( abs(d) < 0.001f ) // 如果等于零做近似处理,abs()用于求绝对值 d = 0.001f ; // 计算参量s,t s = d1/d ; t = d2/d ; // 判断是否发生碰撞 // 如果发生了就返回true if( 0.0f <= s && 1.0f >= s && 0.0f <= t && 1.0f >= t ) return true ; } // for( int i = 0 ; i < 8-1 ; ++i ) // 没有发生碰撞,返回false return false ; } // end of function // 现在对函数做测试 // 初始化质点 x = 10.0f , y = 8.0f ; vx = vy = (float)(rand()%4+1) ; // 进入主循环中 // 假设现在已经在主循环中 if( CollisionTest() ) { // 如果物体与质点发生碰撞 x = 10.0f , y = 8.0f ; vx = vy = (float)(rand()%4+1) ; } // 质点移动 x+=vx ; y+=vy ;