<1>简单的2-D追踪
Andre Lamothe说:“向量几何是游戏程序员最好的朋友”。一点不假,向量几何在游戏编程中的地位不容忽视,因为在游戏程序员的眼中,显示屏幕就是一个坐标系,运动物体的轨迹就是物体在这个坐标系曲线运动结果,而描述这些曲线运动的,就是向量。使用向量可以很好的模拟物理现象以及基本的AI。
现在,先来点轻松的,复习一下中学知识。
向量v(用粗体字母表示向量)也叫矢量,是一个有大小有方向的量。长度为1的向量称为单位向量,也叫幺矢,这里记为E。长度为0的向量叫做零向量,记为0,零向量没有确定方向,换句话说,它的方向是任意的。
一、向量的基本运算
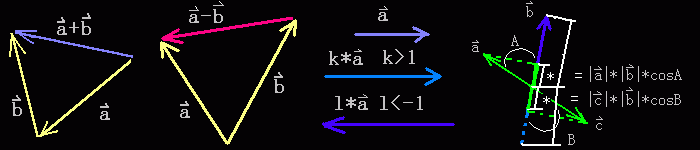
1、向量加法:a+b等于使b的始点与a的终点重合时,以a的始点为始点,以b的终点为终点的向量。
2、向量减法:a-b等于使b的始点与a的始点重合时,以b的终点为始点,以a的终点为终点的向量。
3、 数量乘向量:k*a,k>0时,等于a的长度扩大k倍;k=0时,等于0向量;k<0时,等于a的长度扩大|k|倍然后反向。
4、向量的内积(数量积、点积): a.b=|a|*|b|*cosA 等于向量a的长度乘上b的长度再乘上a与b之间夹角的余弦。
它的几何意义就是a的长度与b在a上的投影长度的乘积,或者是b的长度与a在b上投影长的乘积,它是一个标量,而
且可正可负。因此互相垂直的向量的内积为0。

5、向量的矢积(叉积): a x b = |a|*|b|*sinA*v = c, |a|是a的长度,|b|是b的长度,A是a和b之间的不大于180的夹角,v是与a,b所决定的平面垂直的幺矢,即axb与a、b都垂直。在右手坐标系下,a,b,c构成右手系,即右手拇指伸直,其余四指按由a到b的不大于180度的角卷曲,此时拇指所指方向就是c的方向。因此axb!=bxa。如果是左手系,那么上图中a x b = -c ,即a,b和-c构成左手系。a x b的行列式计算公式如上图右边所示。两个向量的矢积是一个向量。
6、正交向量的内积:互相垂直的两个向量是正交的,正交向量的内积为零。a.b = |a|.|b|*cos(PI/2) = |a|.|b|*0 = 0。
二、向量的性质
没有下面的这些性质做基础,我们后面向量技巧的推导将无法进行。
1) a + b = b + a
2) (a + b) + c = a + (b + c)
3) a + 0 = 0 + a = a
4) a + (-a) = 0
5) k*(l*a) = (k*l)*a = a*(k*l)
6) k*(a + b) = k*a + k*b
7) (k + l)*a = k*a + l*a
8) 1*a = a
9) a.b = b.a
10)a.(b + c) = a.b + a.c
11)k*(a.b) = (k*a).b = a.(k*b)
12)0.a = 0
13)a.a = |a|^2
三、自由向量的代数(分量)表示
1、向量在直角坐标中的代数表示方法:
a=(x,y)
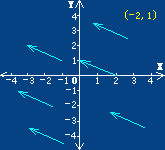
其中x,y分别是向量在x轴和y轴上的分量。任何一个在直角坐标轴上的分量为(x,y)的向量都相等。比如上图中的每个向量都表示为(-2,1)。
或者写成a=x*i+y*j,即i和j的线性组合,这里i是x轴方向的单位向量(1,0),j是y轴方向的单位向量(0,1),因此i正交于j。任意一个2-D向量都可以表成i与j的线性组合。
|i| = |j| = 1
2、向量的代数(分量)表示的运算:
向量加法分量表示:a+b=(xa,ya)+(xb,yb)=(xa+xb,ya+yb)
向量减法分量表示:a-b=(xa,ya)-(xb,yb)=(xa-xb,ya-yb)
向量的内积(数量积、点积)分量表示:
a.b
=(xa * i + ya * j).(xb * i + yb * j)
= xa * i * xb * i + xa * i * yb * j + ya * j * xb * i + ya * j * yb * j
=(xa * xb) * (i * i) + (xa * yb) * (i * j) + (xb * ya) * (i * j) + (ya * yb) * (j * j)
= xa * xb + ya * yb
3、向量长度(模)的计算以及单位化(归一化):
设a=(x,y),则
|a| = |(x,y)| = |x*i + y*j| = sqrt(x^2*i^2 + y^2*j^2) = sqrt(x^2 + y^2),这里sqrt是开平方符号。
a的单位向量为a/|a|,即(x,y)/sqrt(x^2 + y^2)。
四、简单的2-D追踪
现在,有了向量的基本知识,我们就可以分析一个常见的问题-屏幕上一点到另一点的追踪,其实这一问题也可理解为画线问题,画线的算法有很多:DDA画线法、中点画线法以及高效的Bresenham算法。但这些算法一般只是画一些两端固定的线段时所使用的方法,再做一些动态的点与点之间的跟踪时显得不很灵活。使用向量的方法可以很好的解决此类问题。
现在假设你正在编写一个飞行射击游戏,你的敌人需要一种很厉害的武器-跟踪导弹,这种武器在行进的同时不断的修正自己与目标之间的位置关系,使得指向的方向总是玩家,而不论玩家的位置在哪里,这对一个水平不高的玩家(我?)来说可能将是灭顶之灾,玩家可能很诧异敌人会拥有这么先进的秘密武器,但对于你来说只需要再程序循环中加入几行代码,它们的原理是向量的单位化和基本向量运算。
首先我们要知道玩家的位置(x_player, y_player),然后,我们的导弹就可以通过计算得到一个有初始方向的速度,速度的方向根据玩家的位置不断修正,它的实质是一个向量减法的计算过程。速度的大小我们自己来设置,它可快可慢,视游戏难易度而定,它的实质就是向量单位化和数乘向量的过程。具体算法是:导弹的更新速度(vx_missile, vy_missile) = 玩家的位置(x_player, y_player) - 导弹的位置(x_missile, y_missile),然后再对(vx_missile, vy_missile)做缩小处理,导弹移动,判断是否追到玩家,重新更新速度,缩小...
看一下这个简单算法的代码:
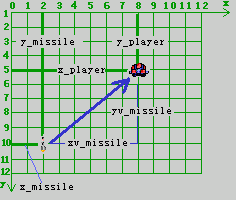
// 假设x_player,y_player是玩家位置分量
// x_missile,y_missile是导弹位置分量
// xv_missile,yv_missile是导弹的速度分量
// 让我们开始吧!
float n_missile ; // 这是玩家位置与导弹位置之间向量的长度
float v_rate ; // 这是导弹的速率缩放比率
// 计算一下玩家与导弹之间的位置向量
xv_missile = x_player-x_missile ; // 向量减法,方向由导弹指向玩家,x分量
yv_missile = y_player-y_missile ; // y分量
// 计算一下它的长度
n_missile = sqrt( xv_missile*xv_missile + yv_missile*yv_missile ) ;
// 归一化导弹的速度向量:
xv_missile /= n_missile ;
yv_missile /= n_missile ;
// 此时导弹的速率为1,注意这里用速率。
// 导弹的速度分量满足xv_missile^2+yv_missile^2=1
// 好!现在导弹的速度方向已经被修正,它指向玩家。
// 由于现在的导弹速度太快,为了缓解一下紧张的气氛,我要给导弹减速
v_rate = 0.2f ; // 减速比率
xv_missile *= v_rate ; // 这里的速率缩放比率,你可以任意调整大小
yv_missile *= v_rate ; // 可以加速:v_rate大于1;减速v_rate大于0小于1,这里就这么做!
// 导弹行进!导弹勇敢的冲向玩家!
x_missile += xv_missile ;
y_missile += yv_missile ;
// 然后判断是否攻击成功
现在,你编写的敌人可以用跟踪导弹攻击玩家了。你也可以稍加修改,变为直线攻击武器。这样比较普遍。
基本的跟踪效果用向量可以很好的模拟。