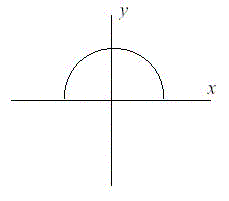《ACM国际大学生程序设计竞赛题解Ⅰ》——基础编程题

  这个专栏开始介绍一些《ACM国际大学生程序设计竞赛题解》上的竞赛题目，读者可以配合zju/poj/uva的在线测评系统提交代码(今天zoj貌似崩了)。

  其实看书名也能看出来这本书的思路，就是一本题解书，简单暴力的通过题目的堆叠来提升解决编程问题的能力。

  那么下面开始探索吧。

  poj1037：

Description

Background
For years, computer scientists have been trying to find efficient solutions to different computing problems. For some of them efficient algorithms are already available, these are the "easy" problems like sorting, evaluating a polynomial or finding the shortest path in a graph. For the "hard" ones only exponential-time algorithms are known. The traveling-salesman problem belongs to this latter group. Given a set of N towns and roads between these towns, the problem is to compute the shortest path allowing a salesman to visit each of the towns once and only once and return to the starting point.
Problem
The president of Gridland has hired you to design a program that calculates the length of the shortest traveling-salesman tour for the towns in the country. In Gridland, there is one town at each of the points of a rectangular grid. Roads run from every town in the directions North, Northwest, West, Southwest, South, Southeast, East, and Northeast, provided that there is a neighbouring town in that direction. The distance between neighbouring towns in directions North-South or East-West is 1 unit. The length of the roads is measured by the Euclidean distance. For example, Figure 7 shows 2 * 3-Gridland, i.e., a rectangular grid of dimensions 2 by 3. In 2 * 3-Gridland, the shortest tour has length 6.  Figure 7: A traveling-salesman tour in 2 ? 3-Gridland.

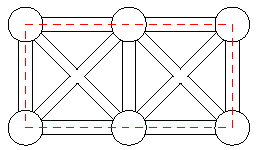
  题目大意：给出一个nxm的矩阵，现在从某点开始遍历所有点并回到起始点，问最少的遍历路程是多少？(从某点出发有8个方向，行上相邻的点之间的距离是1。)

  数理分析：其实这道题目的描述非常有误导性，多次强调所谓“旅行销售员问题”，也就是当现在还没有得到很好解决的著名的TSP问题，这就很容易将人带向很混乱的思维。但是这道题目基于比较特殊的矩阵图，我们应该能够更加简单的方法。

  我们首先应该考虑到的一个贪心策略，行走距离为1的利益最大化就是访问到了一个节点(当然不算起始节点)，那么如果有这样一种方案使得我们，遍历距离+1，都会导致多访问了1个节点，那么这最终一定会导致最小的路程，即节点个数mn。

  那么下面我们所关注的问题便是，是否存在这样一个策略呢？如果m列是偶数，那么连接相邻节点形成小正方格，就会形成奇数列个小方格，这使得我们能够有一个走“S”型的锯齿状的遍历策略，能够使我们完成贪心策略。

  即我们能够得到结论，如果m、n当中有一个是偶数，最小距离都是mn。

  那么如果m、n都是奇数呢？依然从m列入手，我们基于(m-1)xn这样一个矩阵，那么我们可以采取和上面类似的思路进行贪心化的遍历，由此我们其实能够看到，对于这种情况，是没有一种路程为mn的便利方案的，但对于剩下的两列，一开始我们令遍历路线走一个长为1.41的“斜边”，然后由原来的纵向S型变成横向S型，即路程为mn + 0.41，这是除去路程为mn的最优方案。

  上文给出的文字描述可能过于抽象，读者可以自行画图感受一下。

  综合起来我们能够得到这道问题线性算法：

  m、n存在一个偶数，结果是mn。

  否自，结果是mn + 0.41.

  简单的参考代码如下：

#include<cstdio>
using namespace std;

int main()
{
     int t;
     scanf("%d",&t);
     int tt  =1;
     while(t--)
     {
          int n , m;
          scanf("%d %d",&n,&m);
          if(n % 2 == 0 || m%2 == 0)
                printf("Scenario #%d:
%d.00
",tt++,m*n);
          else
                printf("Scenario #%d:
%d.41
",tt++,m*n);

          printf("
");
     }
}

 poj1003:

Description

How far can you make a stack of cards overhang a table? If you have one card, you can create a maximum overhang of half a card length. (We're assuming that the cards must be perpendicular to the table.) With two cards you can make the top card overhang the bottom one by half a card length, and the bottom one overhang the table by a third of a card length, for a total maximum overhang of 1/2 + 1/3 = 5/6 card lengths. In general you can make n cards overhang by 1/2 + 1/3 + 1/4 + ... + 1/(n + 1) card lengths, where the top card overhangs the second by 1/2, the second overhangs tha third by 1/3, the third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table by 1/(n + 1). This is illustrated in the figure below.

 

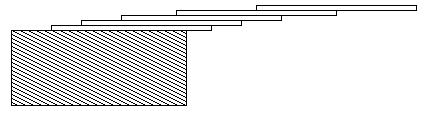
  题目大意：给出一个距离dis，表示堆在桌子上的扑克的伸出距离，问你至少需要多少张扑克能够堆出这个伸出距离。

  数理分析：其实这道题目的描述就是给出了我们的解题方法，它告诉我们n张扑克能够伸出的最远距离是∑1/i，i∈[2,i+1]，这就使得问题变得简单了很多。但是这个问题的原始模型其实是基于长度为2、质量为1的扑克的条件，它其实是调和数的基本模型。如果读者有兴趣看一看这个计算公式怎么得来的，可以看一下笔者的《<具体数学>——特殊的数》一文中关于调和数的介绍。

  参考代码如下。

#include<cstdio>
using namespace std;

int main()
{
     double dis;
     double temp,j;
     int i;
     while(scanf("%lf",&dis)!=EOF && dis != 0.00)
     {
                temp = 0;
              for(i = 2;;i++)
              {
                   j = (double)i;
                   temp += 1/j;
                      if(temp >= dis)
                           break;
              }

         printf("%d card(s)
",i-1);

     }
}

poj1005：

Description

Fred Mapper is considering purchasing some land in Louisiana to build his house on. In the process of investigating the land, he learned that the state of Louisiana is actually shrinking by 50 square miles each year, due to erosion caused by the Mississippi River. Since Fred is hoping to live in this house the rest of his life, he needs to know if his land is going to be lost to erosion.
After doing more research, Fred has learned that the land that is being lost forms a semicircle. This semicircle is part of a circle centered at (0,0), with the line that bisects the circle being the X axis. Locations below the X axis are in the water. The semicircle has an area of 0 at the beginning of year 1. (Semicircle illustrated in the Figure.)

  题目大意：给出某点坐标(x,y)，然后图示半圆从0开始，一年面积增加50，问多少年之后(x,y)会落在半圆上或者内部。

  数理分析：这道题目只要读出半圆每年增加50这个关键条件，然后注意输出的语句格式，其余的部分并不困难。

  参考代码如下：

 

#include<cstdio>
#include<cmath>
using namespace std;
const double pi = 3.1415926;

int main()
{
 double x , y , r;
 int t,i;
 scanf("%d",&t);
 int tt = 1;
 while(t--)
 {
    double temp = 0;
    scanf("%lf%lf",&x,&y);
       r = x*x + y*y;
      for(i = 1;;i++)
      {
            temp = (double)i*100/pi;
               if(temp >= r)
                   break;
      }
      printf("Property %d: This property will begin eroding in year %d.
",tt++,i);
 }
 printf("END OF OUTPUT.");

}

tju1193：

When Issac Bernand Miller takes a trip to another country, say to France, he exchanges  his US dollars for French francs. The exchange rate is a real number such that  when multiplied by the number of dollars gives the number of francs. For example,  if the exchange rate for US dollars to French francs is 4.81724, then 10 dollars  is exchanged for 48.1724 francs. Of course, you can only get hundredth of a franc,  so the actual amount you get is rounded to the nearest hundredth. (We'll round  .005 up to .01.) All exchanges of money between any two countries are rounded  to the nearest hundredth. 

Sometimes Issac's trips take him to many countries and he exchanges money from   one foreign country for that of another. When he finally arrives back home,   he exchanges his money back for US dollars. This has got Issac thinking about   how much if his unspent US dollars is lost (or gained!) to these exchange rartes.   You'll compute how much money Issac ends up with if he exchanges it many times.   You'll always start with US dollars and you'll always end with US dollars.

Input

The first 5 lines of input will be the exchange rates between 5 countries,   numbered 1 through 5. Line i will five the exchange rate from country i to each   of the 5 countries. Thus the jth entry of line i will give the exchange rate   from the currency of country i to the currency of country j. the exchange rate   form country i to itself will always be 1 and country 1 will be the US. Each   of the next lines will indicate a trip and be of the form

N c1 c2 ... cn m

Where 1 ≤ n ≤ 10 and c1, ..., cn are integers from 2 through 5 indicating   the order in which Issac visits the countries. (A value of n = 0 indicates end   of input, in which case there will be no more numbers on the line.) So, his   trip will be 1 -> c1 -> c2 -> ... -> cn -> 1. the real number m   will be the amount of US dollars at the start of the trip.

Output

Each trip will generate one line of output giving the amount of US dollars   upon his return home from the trip. The amount should be fiven to the nearest   cent, and should be displayed in the usual form with cents given to the right   of the decimal point, as shown in the sample output. If the amount is less than   one dollar, the output should have a zero in the dollars place.

  题目大意：一次给出序号为1、2、3、4、5这5个国家之间的货币汇率，然后给出周游顺序<c1,c2,c3...cn>，每到一个国家，我们都将原有的外币换成这个国家的钱，那么给出初始金额m的情况下，完成<1,c1,...cn,1>，最终手头的钱会变成多少，结果应四舍五入至百分位。

  数理分析：在理解了题意之后，能够看到这是一道很基础的模拟题目。需要注意的细节是，所谓四舍五入至百分位，是要求每次交换都按照这个要求，而不是得到最终的money然后四舍五入，二者在多次交换后会产生可见的误差。第3组数据就是明显的例子。

  简单的参考代码如下：

#include<cstdio>
using namespace std;

double rate[6][6];
int country[15];

int main()
{
     int t,n;

           for(int i = 1;i <= 5;i++)
               for(int j = 1;j <= 5;j++)
                  scanf("%lf",&rate[i][j]);

            double money;
            while(scanf("%d",&n) && n != 0)
            {


            country[n+2] = 1;
            country[1] = 1;
            for(int i  = 2;i <= n + 1;i++)
                   scanf("%d",&country[i]);
                scanf("%lf",&money);
            for(int i = 1;i <= n + 1;i++)
            {
                  money *= rate[country[i]][country[i+1]];
                  money = (int)(money*100 + 0.5);    //每次交换都应该进行百分位的四舍五入
                  money /= 100;
            }
         printf("%.2lf
",money);
            }

}

poj1046：

Description

A color reduction is a mapping from a set of discrete colors to a smaller one. The solution to this problem requires that you perform just such a mapping in a standard twenty-four bit RGB color space. The input consists of a target set of sixteen RGB color values, and a collection of arbitrary RGB colors to be mapped to their closest color in the target set. For our purposes, an RGB color is defined as an ordered triple (R,G,B) where each value of the triple is an integer from 0 to 255. The distance between two colors is defined as the Euclidean distance between two three-dimensional points. That is, given two colors (R1,G1,B1) and (R2,G2,B2), their distance D is given by the equation

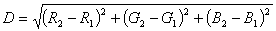
Input

The input is a list of RGB colors, one color per line, specified as three integers from 0 to 255 delimited by a single space. The first sixteen colors form the target set of colors to which the remaining colors will be mapped. The input is terminated by a line containing three -1 values.

Output

For each color to be mapped, output the color and its nearest color from the target set.
If there are more than one color with the same smallest distance, please output the color given first in the color set

 

  题目大意：首先给出16个三元实数对(R,G,B)，然后键盘输入某个三元组(r,g,b)，求解(r,g,b)与这16个当中哪个三元组“距离”最小,距离公式题目中已经给出。

  数理分析：其实这种类型的题目在读出题意之后，将其简化得描述出来，会发现是很基础的题目。

  简单的参考代码如下：

 

#include<cstdio>
using namespace std;

struct color
{
    int  r ,g ,b;
}a[10000];
int main()
{
      for(int i = 1;i <= 16;i++)
          scanf("%d%d%d",&a[i].r,&a[i].g,&a[i].b);


      int rr , gg , bb;
      while(scanf("%d%d%d",&rr,&gg,&bb)  && rr+gg+bb >= 0)
            {
                   int Min = 99999999;
                   int temp , tempi;
                   for(int i = 1;i <= 16;i++)
                      {
                            temp = (a[i].r-rr)*(a[i].r-rr) + (a[i].g-gg)*(a[i].g-gg) + (a[i].b-bb)*(a[i].b-bb);
                            if(temp < Min)
                            {
                                 Min = temp;
                                 tempi = i;
                            }
                      }
                 printf("(%d,%d,%d) maps to (%d,%d,%d)
",rr,gg,bb,a[tempi].r,a[tempi].g,a[tempi].b);
            }
}

zoj1078:

  Statement of the Problem

We say that a number is a palindrom if it is the sane when read from left to right or from right to left. For example, the number 75457 is a palindrom.

Of course, the property depends on the basis in which is number is represented. The number 17 is not a palindrom in base 10, but its representation in base 2 (10001) is a palindrom.

The objective of this problem is to verify if a set of given numbers are palindroms in any basis from 2 to 16.

Input Format

Several integer numbers comprise the input. Each number 0 < n < 50000 is given in decimal basis in a separate line. The input ends with a zero.

Output Format

Your program must print the message Number i is palindrom in basis where I is the given number, followed by the basis where the representation of the number is a palindrom. If the number is not a palindrom in any basis between 2 and 16, your program must print the message Number i is not palindrom.

  题目大意：给出一个十进制数字n，判断n在x进制下是否会问，x∈[2,16]，并输出x。

  数理分析：这道题目分为两个步骤，第一是进制转化，第二是判断回文。判断回文根据其定义进行模拟判断即可，下面说一下如何进行进制转化。

  我们知道，整数x表示成r进制的形式为，x = x1*r^0 + x2*r^1 + x3*r^2 +...，那么我们采取类似快速幂的过程，通过计算x%r，我们能够得到x1，随后我们令x = x/r，再计算x%r将得到x2......依次类推，便可得到r进制数x。

  简单的参考代码如下。

#include<cstdio>
using namespace std;

int main()
{
      int n;
      int i , j;
      while(scanf("%d",&n) && n)
      {
           int sign = 0;
           char c[30];
           int base[17] = {0};
           for(i = 2;i <= 16;i++)
           {
                int m = n;
                int len = 0;
                while(m)
                {
                    c[len++] = m%i;
                    m = m/i;
                }
                sign = 1;
                for(j = 0;j <len/2 &sign ;j++)
                       if(c[j] != c[len-j-1])  sign = 0;
                if(sign)  base[i] = 1;

           }

             sign = 1;
             for(i = 2;i <= 16;i++)
                  if(base[i] == 1)  sign = 0;
             if(sign)
                   printf("Number %d is not a palindrom
",n);
             else
               {
                   printf("Number %d is palindrom in basis",n);
                   for(i = 2;i <= 16;i++)
                           if(base[i] == 1)
                              printf(" %d",i);
                    printf("
");
               }
      }
}