问题一:将一个2003边形的每个顶点染成红、蓝、绿三种颜色之一,使得相邻顶点的颜色互不相同,请问有多少种满足条件的方法?
分析:直接求解似乎不太现实,将多边形的边数看成变量,我们设置T(n)记录方案数,应用简单的组合计数原理,容易看到T(3) = 6 , T(4) = 18。基于这么有限的条件,我们如何求解T(2003)呢?递推似乎是解决这种问题的好方法。
我们考虑基于T(n-1),在第n-1后面再加一个点形成n边形。
如果第1个点和第n-1个点同色,对于第n个顶点我们有2种选择,而对于剩余n-1个顶点,我们基于n-2个顶点的方案数,每次添加一个和第一个顶点相同颜色的点,便完成了所有情况的构造,此时即得到2T(n-2)种方案。
如果第1个点和第n-1个点异色,那么对于第n个顶点我们只有一种方案,便基于T(n-1)的基础上添加一个点即可,我们得到T(n-1)种方案。
由此我们可以得到结论:T(n) = T(n-1) + 2T(n-2),结合初始条件,T(2003)显然是可求的。
如果说我们有台计算机,那么基于上面的条件其实也就可以求解了,但如果没有的话,我们则需要进一步从这个递推式中挖掘信息。
外延一种根据递推式求解通项的方法:对于递推式a(n+2) = pa(n+1) + qa(n),a1 = α,a2 = β,x^2 + px + q = 0是其特征方程的根,x1、x2为特征方程的解。当x1 != x2,an = Ax1^(n-1) + Bx2^(n-1) ;而当x1 = x2 , an = (A + Bn)x^(n-1)。其中A和B通过初始条件a1、a2的值,利用待定系数的方法求解。
那么考察此题给出递推等式,我们可得出an的通项,T(2003)也不难求解了。
问题二:设n是正整数。若由n个正整数组成的数列(可以相同)满足:对于每个正整数k(k >= 2),当k在此数列中时,k - 1也在此数列中,且k-1第一次出现的位置在k最后一次出现的位置的前面,则称该数列为“满的”。问:对于每个整数n,有多少个满的数列?
分析:由题目鉴定,我们可知对于r = max{a1,a2……an},则区间[1,r-1]的整数都在该数列当中,我们设置集合Si来表示数列中第k个元素ak = i的下标k,即Si = {k | ak = i},之所以定义这个集合,是为了方便利用题设条件,由此我们可知min Si-1 < max Si , 则此时我们可以对Si所含元素进行一个简单的排序。
S1 = {b1,b2,……b(k1)} (b1 > b2……>b(k1) 且 b(k1) > b(k1 + 1))
S2 = {b(k1+1) , b(k1 + 2)……b(k2)} (b(k1+1) > b(k1+2)……>b(k2)且b(k2) > b(k2 + 1))
……
由此我们考察S1、S2……Sr不难发现,r个集合的n个元素与{1,2,3……n}满足一个双射关系,那么基于这种双射关系,我们通过{1,2,3……n}形成n!种排列,然后相应的去匹配ak对应的正整数,便可构造出满的数列,由此不难得出该题的结论,对于每个n,有n!个满的数列。
问题三:桌子上有六个空钱包,将12枚2元硬币放入这些钱包中,至多剩余一个钱包,问有多少种方法?
分析:这算是组合计数问题里面比较基础的问题了。题设所说至多剩余一个,即分为没有空钱包和剩余一个空钱包,我们只需要分情况讨论然后将两种情况的结果相加即可。
①没有空钱包,这种情况对应着将6个硬币放入6个钱包(允许有空钱包)的情况,因此在给6个钱包分组的时候,会形成11个位置,分成6组需要选择5个位置,即C(11,5)。
②如果有一个空钱包,首先要选出这个空钱包,即C(6,1),将12个硬币放入5个钱包,对应着将7个硬币放入5个钱包(允许有空钱包)的情况,采取①的思路,我们得到C(13,4)。
综合起来,这道题的解即为C(11,5) + 6C(13,4)。
问题四:设六边形ABCDEF是边长为1的正六边形,O是六边形的中心,除了六边形的每一条边,可以从O到每个顶点连一条线段,共得到12条长度为1的线段,一条路径是指从O出发,沿着线段最后又回到O,问:长度为2003的路径共有多少条?
分析:首先我们应该考虑的是求解这道问题的通式,我们设置a[n]记录长度为n的路径,而b[n]表示从某个顶点出发,到达O的路径的长度。考察该几何图形,我们容易看到如下的递推关系式。
a[n] = 6b[n-1] (考察a[n]路径,去掉其最后一步,得到此递推式)
b[n] = a[n-1] + 2b[n-1](考察b[n]路径,去掉其最后一步,得到递推式)
由此我们不难得出关于a[n]的递推式——a[n+2] - 2a[n+1] - 6a[n] = 0。同样,如果这是一道编程问题,我们基于这个递推式就可以求解了,但是如果是个数学题的话,我们则需要给予这个递推式进一步求其通式,其方法在问题一种已经给出。
此题的关键是寻求这种递推关系,而寻求递推关系的关键则是基于一种状态,通过去掉最后一个步来建立起与前一种状态的联系,而所谓的”去掉最后一步“是否完成的足够全面(没有重复没有漏),则是递推关系是否正确的关键一环。
问题五:将n(n>=1)个有标记的球分别分配给九个人A、B、C、D、E、F、G、H、I,问:有多少种分配方法,使得A得到的球的数目与B、C、D、E一共得到的球的数目相同?
分析:此题是非常考验数学观察力和构造能力的,既然是9个人,A球和另外四个球数量相同,我们考察(x^2 + x + x + x + x + 1 + 1 + 1 + 1)^n这样一个式子。我们规定如果将第k个球给A,那么选取第k个因子中的x^2;如果将第k个球分给B、C、D、E,则选取第k个因子当中的第1、2、3、4个1;如果将第k个球给F、G、H、I,则选取第k个因子中第1、2、3、4个x,我们会看到,为了满足A的球和B、C、D、E的球数和相同,需要选择一个因子的x^2,就要对应选择另一个因子中的某个1,而其余因子只能选择x,由此不难看出,(x^2+4x +4)^n展开式中x^n的系数变式方案的总数。利用牛顿二项式定理,对于(x+2)^2n,x^n的系数为2^nC(2n,n)。
这道题目呈现出来的方法思想,对于学过生成函数算法的读者来说可能比较熟悉。即一种将组合计数和函数表达式联系在一起,通过证明函数与组合计数的等效转化性,然后基于函数进行运算。
问题六:对所有是数字1~7的全排列的七位数,从小到大进行排序。问:数字3654217出现在第几个?
这也是一道比较基础的组合计数问题,我们考虑第一个数字是1、2的情况,得到2*6!个数字;第一个数字是3第二位数字是1、2、4、5,得到4*5!个数字;类似地依次分析接下来的每一位,即,共有2*6! + 4*5! + 3*4! + 2*3! + 1*2! ,在此结果上+1便得到最终结果。
问题七:数916238457是一个包含1~9每个数字恰好一次的九位数的例子,其还具有性质:数1~5以正常的顺序出现,但1~6不以正常的顺序出现。问:这样的数有多少个?
题目很简单,关键点在于理解这个9位数的性质,我们先将1~5排好顺序,形成6个空隙,按照性质,数字6有5个符合要求的空隙,即有5种方法,然后再依次填入7、8、9,则答案为5 * 7 * 8 * 9 = 2520.
问题八:有多少种方法可将2011/2010表示成两个n+1/n(n∈Z)型分数的乘积?(其中,ab和ba认为是一种方法)
我们设2011/2010 = (p + 1)/p * (q + 1)/q,进行整理可得p = 2010 + (2010*2011)/(q - 2010) , q = 2010 + (2010*2011)/(p-2010)。由因为q、p都是正整数,所以p - 2010是2010*2011的因子即可,因此对其进行素因子分解,有2010*2011 = 2 * 3 * 5 * 67 *2011 , 其因子数共有C(5,1) + C(5,2) + C(5,3) + C(5,4) + C(5,5) = 2^5,由于p、q表示形式上的对称性,当存在一组解(p,q)的时候,另外一组解(q,p)也会满足条件,因此这里共有16种方法。
问题九:令f(n)为满足4x+3y+2z = 2000 = n的正整数数对(x,y,z)的个数,求f(2009) - f(2000)。
设4x+3y+2z = 2000 , 观察到2009 - 2000 = 9 , 并且y的系数3是9的因子,因此我们构造x' = x , y' = y + 3 ,z' = z,则有4x' + 3y' + 2z' = 2009,因此我们可以看到在y'的解空间中,y' > 3的时候与y的解空间形成双射,即f(2009) - f(2000)的值为y' = 1 , 2 , 3时可以取的(x,y,z)的整数对的个数。
y' = 1 => 4x' + 2z' = 2006 => 501组。
y' = 2 => 4x' + 2z' = 2003 => 0组。
y' = 3 => 4x' + 2z' = 2000 => 499组。
因此f(2009) - f(2000) = 499 + 501 = 1000.
问题十:从1°、2°……179°选出三个角度使其成为非等腰三角形的三个内角,问:有多少种选法?
我们设三个内角分别是x、y、z,由x + y + z = 180 , 我们能够得到C(179,2)组解,需要知道的是这里的解的组合有次序的,即是一种排列。随后我们需要找到等腰三角形的情况,为了好分析,我们先把等边三角形单独拿出来分析。x、y、z用(x,y,z)来表示。
(60,60,60) , 1组。
(1,1,178) 、(2,2,176)……(89、89、2) , 由于我们求总情况数的时候是一种排列,这里当然需要保持一致,共88C(3,1)组。
求解最终的答案不要忘了去除排列性,即答案为C(179,2) - 1 - 88C(3,1) / A(3,3)。
问题十一:求满足下述条件的正整数的数目,可以被9整除,位数不超过2008,且各位数字中至少有两位数字是9.
总数:利用基本的分步乘法原理,有10^2008 - 1种。(减掉0的情况)
其中9的倍数有(10^2008 - 1)/9种。
现在考虑这些数字各位数字中至多有1个9的情况的数量,然后用总数减掉便可得答案。
(1)有0位9,我们对前2007位在0~8中随机选择,为使这个2008位的整数被9整除,第2008位的数字是唯一确定的,因此这种情况下得到9^2007 - 1种情况.
(2)有1位9,类似上面的过程,在这里我们得到C(2008,1)9^2006种情况。(显然这种情况下是不会出现0的)
因此最终满足题意的数目共有(10^2008 - 1)/9 - (9^2007 - 1) - 2008*9^2006。
问题十二:有六个红球、三个篮球、三个黄球。将这些球放在一条直线上,假设同色的球没有区别。试问:有多少种不同的方法,使得同色的球不相邻?
这其实是组合计数问题中的一类“不相邻”问题,我们应该先将数量较多的球摆好,然后将颜色不同的球插入到其中。在这个问题中,我们首先将6个红球摆好——10101010101(1代表红球,0代表必须填充的间隔),而我们手头还有另外的6个球,因此我们能够知道,蓝色球和黄色球至多相邻一次。那么下面我们便开始分别讨论。
(1)蓝色球和黄色球不相邻:显然有C(2,1)*C(6,3)种情况。
(2)蓝色球和黄色球相邻一次:我们将相邻的蓝色球和黄色球合成一个花球,这种合成包括2种方法,则此时出现的情况数为2 * 5! / (2! * 2! )。
问题十三:15张卡片上分别写着1,2,……15.现从中至少选出一张卡片。问:有多少种选择方式,使得所选的所有卡片上的数均大于或等于被选的卡片的张数?
我们从更加一般的角度来分析这个问题,如果给出了k张卡片,考虑用递推的思维来建立起前后状态的关系,我们进行如下的分类讨论,记f[k]表示:
(1)不选第k张卡片,则得到f[k-1]种情况。
(2)选择了第k张卡片。
(i)不选其余卡片,1种情况。
(ii)选择其余卡片,很容易看到,当前情况就不能够选第1张卡片了,对于剩余的2、3……k-1张,我们将其重新编号:1,2……k-2,可以看到,我们在f[k-2]种情况的基础上,加上第k张卡片,由于增加了一张卡片数,应该将每个卡片的编号+1,这其实刚好与我们进行编号前的所有情况是一一对应的,由此我们得到了f[n-2]种情况。
综合起来,我们发现,f[n] = f[n-1] + f[n-2] + 1,基于这个递推式,我们就很容易进行求解了。
问题十四:设正整数m、n互素,s是任意一个整数,求集合{1,2,3……m+n-1}的子集A的数目,使得|A| = m,且∑x ≡ s(mod n),其中x∈A.
我们容易看到,元素个数为m的子集个数为C(m+n-1,m)种,现在我们需要探讨在这些种集合中,(∑x) mod n的结果是否会出现重复,或者说如何进行重复。
我们基于这样一条数论中结论,如果(p,n) = 1,则n mod p 、2n mod p…… (p-1)n mod p是1、2、……p-1的一个某种次序的排列(证明费马小定理的用到的结论,可用鸽巢原理去证明)。那么现在用到这里,对于某种情况∑xk,我们进行xk <- xk + 1的操作,则∑xk增加了m,那么进行n次这样的操作,结果便是0、1、2……n-1的一个某种次序的排列,那么基于这个结论,我们这个过程放在一个m + n - 1的数环上,对于某个长度为m的集合,旋转n次,∑xk mod n = 1、2、3……n-1,可以看到,所有的情况都会存在与这样一个旋转的系中,因此我们得到结论,∑x ≡ s(mod n),s取0、1、2……n-1的情况数目是相等的,因此该题最终的答案是1/n * C(m+n-1,m).
问题十五(uva 12034):
A、B两个人赛马,最终名次有3种可能:并列第一;A第一B第二;A第二B第一。那么按照这种排名方法,给出整数n,求解最终排名的所有情况数。
分析:考虑基本的递推原理就能够得到这道问题的解,设dp[n]是n个人不同排名的情况数,选择i个人成为并列第1,完成问题规模的削减,然后将各个情况累加起来,可以得到如下的状态转移方程:
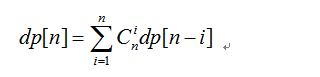
#include<cstdio> using namespace std; const int MOD = 10056; const int maxn = 1005; int dp[maxn]; int C[maxn][maxn]; void init() { for(int i = 0;i < maxn;i++) { C[i][0] = 1; for(int j = 1;j <= i;j++) C[i][j] = (C[i-1][j-1] + C[i-1][j]) % MOD; } } int main() { init(); dp[0] = 1; dp[1] = 1; dp[2] = 3; int n; int T; int tt = 1; for(int i = 3;i <= maxn;i++) { int sum = 0; for(int j = 1;j <= i;j++) { sum += (C[i][j]*dp[i-j])%MOD; //printf("%d ",(C[i][j]*dp[i-j])); } dp[i] = sum%MOD; } scanf("%d",&T); while(T--) { scanf("%d",&n); printf("Case %d: ",tt++); if(n == 1 || n == 2) {printf("%d ",dp[n]);continue;} printf("%d ",dp[n]); } }
问题十六(uva 10213):
有多少土地:
在一个椭圆的土地当中,在边界上有n个点,现在连接任意的两个点,那么请问这块椭圆土地能够最多被分割成多少块?
分析:一道欧拉定理即视感非常强的题目,我们依然要借助节点v、边的个数e来确定面数f,在这里要去掉最外面那个面,即在这道具体的题目当中,f = e-v+1.
那么下面的问题还是求v、e。其实这里能够看到已经和计算几何不沾什么边了,本质上来讲是一个组合计数问题。
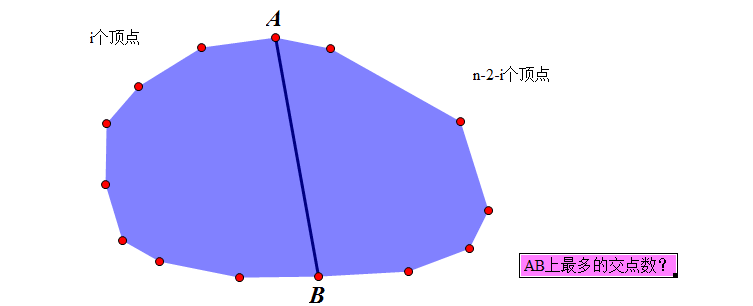
点:
我们固定一条线段的起始点,然后遍历剩余点作为终点,状态参量i表示该线段左边的点的个数,这是一个子问题,我们遍历起始点,然后进行去重(充分理解这个分割状态的过程,能够看到每个点会被计算4次)就可以了。
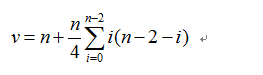
边:
基于求点数的穷举计数方法,这里计算边会变得非常简单。
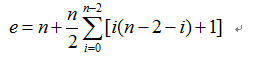
但是很遗憾这个问题到这里还没有结束,由于这道题目是多组数据,而且在时间复杂度上卡的很近,因此我们需要继续的化简。

对于一个样例,给出n,我们给出的公式是O(n)算法(循环计算),下面尝试将其优化成O(1)。
参考代码如下:
import java.math.BigInteger; import java.util.Scanner; public class main { public static void main(String[] args) { int t; Scanner in = new Scanner(System.in); t = in.nextInt(); for(int Case =1 ;Case <= t;Case++) { BigInteger n = in.nextBigInteger(); BigInteger a = n.pow(4); BigInteger b = n.pow(3).multiply(BigInteger.valueOf(6)); BigInteger c = n.pow(2).multiply(BigInteger.valueOf(23)); BigInteger d = n.multiply(BigInteger.valueOf(18)); BigInteger ans = BigInteger.valueOf(0); ans = ans.add(a).subtract(b).add(c).subtract(d); ans = ans.divide(BigInteger.valueOf(24)); ans = ans.add(BigInteger.valueOf(1)); System.out.println(ans); } } }