与Logistuc Regression相比,SVM是一种优化的分类算法,其动机是寻找一个最佳的决策边界,使得从决策边界与各组数据之间存在margin,并且需要使各侧的margin最大化。比较容易理解的是,从决策边界到各个training example的距离越大,在分类操作的差错率就会越小。因此,SVM也叫作Large Margin Classifier。
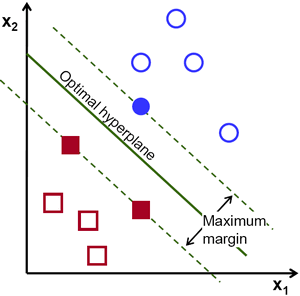
最简单的情况是,在二维平面中的,线性可分情况,即我们的training set可以用一条直线来分割称为两个子集,如下图所示。而在图中我们可以看到,H2和H3都可以正确的将training set进行分类,但细细想来,使用H2进行分类的话,我们对于靠近蓝线的几个训练样例其实是不敢说100%的,但对于离蓝线最远的小球,我们却很有把握。这也是H3这条SVM红线出现的原因:尽量让两侧的训练样例远离决策边界,从而让我们的分类系统有把握对每个球Say Absolutely。

在Logistic Regression中,我们将类别y定义为0和1,从而把h(x)看做p(y=1)的概率,而在SVM里,我们将其定义为-1和+1。而我们所需要在n维空间中寻找的超平面,则被定义为:

由此,分类函数可以定义为:

将training example的坐标带入可以得到三种结果:f(x)=0,则该点处于决策平面上;f(x)>0,属于y=1类;f(x)<0,属于y=-1类。而对于每个训练样例,我们可以通过计算如下定义的“函数间隔”(functional margin),来判断是否分类正确(数值为负则说明错误),以及通过数值大小看出测试点与决策平面的距离:

而真正表征SVM决策边界margin宽窄的,是上式中值最小的那个,也就是说,距离边界最近的点,其到边界的距离,决定了margin的大小。

而上式得出的函数间隔,实际上并不是该间隔真正的长度值,所以我们需要计算“几何间隔”(geometric margin),即点到平面距离公式:


带入SVM公式,的几何间隔计算公式:

此时,我们想要做的事情是,最大化这个几何距离:
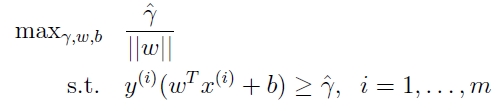
那么,如此看来,我们已经ok了,如下图:
我们现在得到的三个hyperplane的方程为:
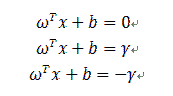
在这种情况下,margin是多少呢,根据平行线的距离公式:
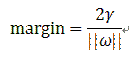
在这里其实我纠结了很长时间,因为很多课程从此就说的不太详细了,也许是我个人的数学水平较差吧,所以就花了很久去思考。首先,我们考虑到这个几何距离gamma,肯定是一个常数,因为当我们的f(x)确定,数据集确定以后,它就是离f(x)最近的点到f(x)=0这条直线的距离。那么,我们上述的三个方程,同时除以一个常数,一切会改变吗?首先,可以确定,3个方程一点也不会变,2x+4=6与x+2=3,是一样的对吗?那么我当时就想了,这波操作后,margin肯定会变的!实际上,由于gamma和w之间的线性关系,margin也是不变的,所以相当于,我们修改了w,从而消去了gammar。
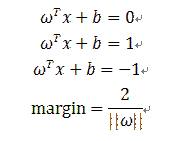
而单边的margin则等于总margin的一半:
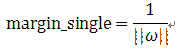
则问题转化为:
