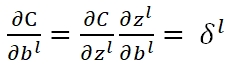在下图所示的Neural Network中,我们将拥有三个节点的layer1及layer4分别称为输入和输出层,而中间的两层layer2,layer3称为隐藏层(hidden layer)。输入数据X,从左侧进入神经网络,经过层层传播最终从右侧输出的过程,称为Feedforward。而根据training set来调整参数的算法,称为Backpropagation Algorithm,即反向传播算法。

在Hidden layer的每个Node中,都存在一个non-linear unit,常用的是有tanh,sigmoid以及ReLu等。如果没有non-linear unit,则无论NN的architecture如何,输出将永远是输入数据的线性组合,Neural Network也就失去了意义。
首先我们约定weight的表达方式如下图所示:

每个节点的左侧输入值z等于:

每个节点的右侧输出值a等于在其输入值z的基础上,施加非线性可微函数σ

假设Neural Network总共有L层,则会有L-1个ω矩阵存在,所以ω矩阵的维度是size(ω)=q*p,其中q为下一层的节点数,p为本层的节点数。在上图的Layer3中,w3为如下的2x4的矩阵形式:

如果将Feedforward propagation的过程矩阵化,则可以写为:

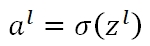
下面来看如何使用Backpropagation更新ω呢。Backpropagation其实是Gradient Descent的一种拓展,如果我们能够拿到cost function对某个ω的梯度值,那么我们就可以对其做梯度下降并迭代求出最优结果。更新算法见:线性回归与梯度下降
为了说明方便,一般会定义一个δ作为某一个节点输入端的误差(即z值的误差):

矩阵化后:
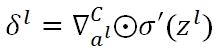
我们可以根据上式,直接算出最后一层的δ值,但是对于任意一层、任意一个节点的δ,则需要将最后一层的误差值进行层层传导,其公式为:
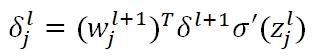
矩阵化后,任意一层的节点误差矩阵为
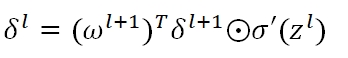
而我们最终的目的在于求得w的梯度,从而利用gradient descent去更新参数,对于任意一层l的某条路径j,k,我们有:

对任意一层l的所有weight,我们有:
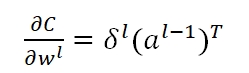
对于第l层bias处的梯度: