转载:http://www.cnblogs.com/jingmoxukong/p/4311237.html
要点
基数排序与本系列前面讲解的七种排序方法都不同,它不需要比较关键字的大小。
它是根据关键字中各位的值,通过对排序的N个元素进行若干趟“分配”与“收集”来实现排序的。
不妨通过一个具体的实例来展示一下,基数排序是如何进行的。
设有一个初始序列为: R {50, 123, 543, 187, 49, 30, 0, 2, 11, 100}。
我们知道,任何一个阿拉伯数,它的各个位数上的基数都是以0~9来表示的。
所以我们不妨把0~9视为10个桶。
我们先根据序列的个位数的数字来进行分类,将其分到指定的桶中。例如:R[0] = 50,个位数上是0,将这个数存入编号为0的桶中。
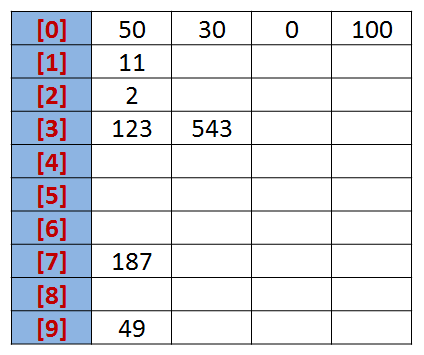
分类后,我们在从各个桶中,将这些数按照从编号0到编号9的顺序依次将所有数取出来。
这时,得到的序列就是个位数上呈递增趋势的序列。
按照个位数排序: {50, 30, 0, 100, 11, 2, 123, 543, 187, 49}。
接下来,可以对十位数、百位数也按照这种方法进行排序,最后就能得到排序完成的序列。
算法分析
基数排序的性能
|
排序类别 |
排序方法 |
时间复杂度 |
空间复杂度 |
稳定性 |
复杂性 |
||
|
平均情况 |
最坏情况 |
最好情况 |
|||||
|
基数排序 |
基数排序 |
O(d(n+r)) |
O(d(n+r)) |
O(d(n+r)) |
O(n+r) |
稳定 |
较复杂 |
时间复杂度
通过上文可知,假设在基数排序中,r为基数,d为位数。则基数排序的时间复杂度为O(d(n+r))。
我们可以看出,基数排序的效率和初始序列是否有序没有关联。
空间复杂度
在基数排序过程中,对于任何位数上的基数进行“装桶”操作时,都需要n+r个临时空间。
算法稳定性
在基数排序过程中,每次都是将当前位数上相同数值的元素统一“装桶”,并不需要交换位置。所以基数排序是稳定的算法。